OS-E: 0805 Two-dimensional Michell-truss
The two-dimensional Michell-truss is an optimal topology structure generated under bending.
Model Files
Refer to Access the Model Files to download the required model file(s).
The model file used in this example includes:
michell.fem
Model Description
The design space for this problem consists of a rectangle with a single vertical load at the free end. A circular cut-out is constrained in all translational degrees-of-freedom on the inside free edge.
This is a compliance minimization problem with a material volume fraction constraint of 20%. CQUAD4 (4-noded isoparametric) elements are used in a design space defined by a rectangular region with an aspect ratio approximately equal to one quarter of the short edge located closer to the edge away from the load.
DESGLB = 2
$
SUBCASE 1
SPC = 1
LOAD = 2
DESOBJ = 1BEGIN BULK
$
DRESP1,1,comp,COMP
DRESP1,2,volfrac,VOLFRAC
DCONSTR,2,2,,0.2
Figure 1. Finite Element Mesh of the Design Space for the Two-dimensional Michell-truss
This example is analyzed using the one-file setup with the file,
michell.fem. The OptiStruct
batch job is submitted using the command shell script, % optistruct
michell.
Results
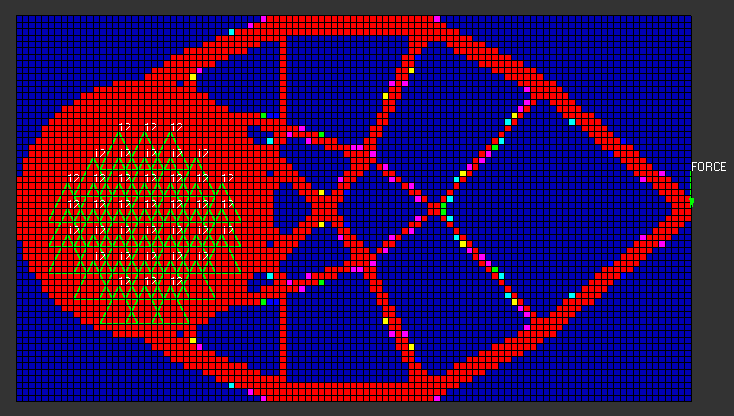
Figure 2. Contour Plot of Density Results for the Two-dimensional Michell-truss