EN法では、塑弾性ひずみの結果を使用してひずみ寿命解析を実行します。
切り欠き底部のような重要な箇所の多くには応力が集中し、疲労破壊に至る前の繰り返し荷重の期間では塑性変形することが明らかです。ひずみ寿命解析は、この点を踏まえた解析手法です。ひずみ寿命解析では塑性ひずみ結果が不可欠です。
Neuber補正
弾塑性結果を考慮して弾性解析結果を補正する場合は、Neuber補正が最も広く使用されています。
入手が容易な公称応力から局所応力を導くには、局所応力集中係数
や局所ひずみ集中係数
などの集中係数を使用します。
(1)
(2)
は局所応力、
は局所ひずみ、Sは公称応力、eは公称ひずみです。公称応力と局所応力の両方が弾性であれば、局所応力集中係数は局所ひずみ集中係数に等しくなります。しかし、塑性ひずみが存在すると、
と
とのこの関係は保持されなくなります。Neuberはこの点に注目し、理論上の弾性応力集中係数
を提唱しました。
(3)
式 1と式 2を式 3に代入すると、理論上の応力集中係数
は次のように書き換えることができます。
(4)
線形静解析では公称応力ではなく、局所応力が得られます。これによって、式 4ではジオメトリによる効果がなくなり、
を1とすることができるので、式 4を次のように書き換えることができます。
(5)
と
は、それぞれ弾性解析から得られる局所弾性応力と局所弾性ひずみ、
と
は、それぞれ塑性ひずみが存在する場合の応力とひずみです。
と
の両方は、繰り返し応力ひずみ曲線とヒステリシスループも使用してEq.9から計算できます。
繰り返し応力ひずみ曲線
繰り返し荷重を受けている材料は、単調荷重の場合とは異なる挙動を示します。一般的に、その応答には次の4種類があります:
- 定常状態
- 繰り返し硬化
- 繰り返し軟化
- ひずみ範囲に応じて軟化または硬化
どの応答が発生するかは、材料の性質と熱処理の初期条件によります。繰り返し硬化と繰り返し軟化の効果を次の図に示します。ここでは、2種類の材料で見られた最初の2回のヒステリシスループをプロットしています。どちらの場合も、ひずみは一定の範囲で変化するように制限され、応力は自由に変化するようになっています。
材料の繰り返し応答(a)のように、一定範囲のひずみの下で、前のサイクルよりも応力振幅が大きくなる状態を繰り返し硬化と呼び、応力振幅が小さくなる状態を繰り返し軟化(b)と呼びます。
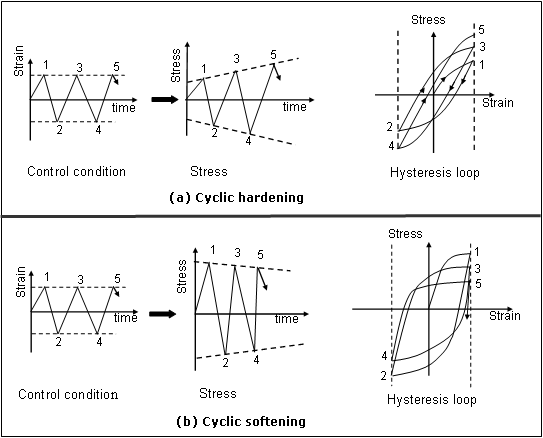
図 1. 材料の繰り返し応答: (a)繰り返し硬化、(b)繰り返し硬化
ひずみを制限しない状態での応力振幅を指定することによって、材料の繰り返し応答を記述することもできます。一定範囲の応力の下で、前のサイクルよりもひずみ振幅が大きくなる状態を繰り返し軟化と呼び、ひずみ振幅が小さくなる状態を繰り返し硬化と呼びます。材料の挙動は短時間の後に定常状態に達しますが、実際のところ、その状態が材料の総寿命に占める期間は10%未満にすぎないことが普通です。さまざまなひずみ振幅を指定しても、定常状態における複数のヒステリシスループを得ることができます。
図 2のように1つの座標系にこれらのヒステリシスループを配置すると、ループのすべての頂点を結ぶラインによって繰り返し応力ひずみ曲線が得られます。
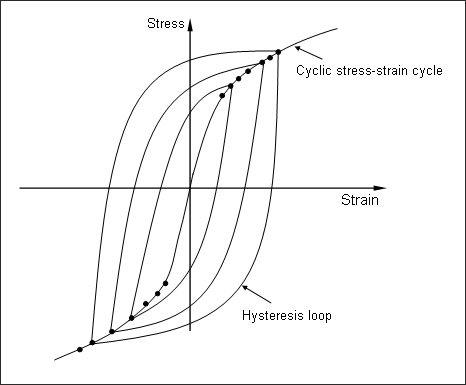
図 2. 定常応力ひずみ曲線の定義
これは、次のように単調応力ひずみ曲線と同様な形式で表現できます。
(6)
ヒステリシスループの形状
初期荷重で材料に塑性ひずみが発生した後、逆方向の荷重をかけると材料が異方性の挙動を示すことをBauschingerが発見しました。Massingは、実験的な証拠に基づき、応力ひずみヒステリシスループは、繰り返し応力ひずみ曲線と形状は類似しているものの、振幅は2倍になるという仮説を提唱しました。つまり、
の値が
の2倍であれば、応力ひずみ曲線がヒステリシスループに重なることになります。これを式で表現すると次のようになります。
(7)
(8)
を
で表現し、
を
,で表現して、それを式 6に代入すると、ヒステリシスループの式は次のようになります。
(9)
応力を制限した状態で応力と疲労寿命を対数スケールにプロットすると両者が比例関係になることを、ほぼ1世紀前にBasquinが発見しました。Basquinは、応力を変数とする、次の疲労の式を提唱しています。
(10)
は応力振幅、
は疲労強度係数、bは疲労強度指数です。その後、塑性ひずみも次の簡潔な指数法則によって疲労寿命と関係している可能性があることを、1950年代にCoffinとMansonが別々に提唱しました。
(11)
は塑性ひずみ振幅、
は疲労延性係数、は疲労延性指数です。Basquin、Coffin、Mansonによる成果をMorrowが統合し、疲労寿命に対する弾性ひずみと塑性ひずみ双方の影響を検討しました。Morrowは、疲労寿命に対して総ひずみがより強い相関関係を持つことを見出しています。フックの法則を適用すると、Basquinによる法則を次のように書き換えることができます。
(12)
は弾性ひずみ振幅です。したがって、弾性ひずみと塑性ひずみの和である総ひずみ振幅は、Basquinによる式およびCoffinとMansonによる式を適用して次のように記述できます。
(13)
は総ひずみ振幅で、他の変数は前記の式と同様です。
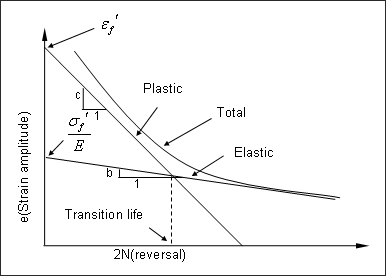
図 3. 対数スケールにプロットしたひずみ寿命曲線


