周期カウントを使用して、ランダムな荷重シーケンスから、離散的で簡潔ながらも“等価”な一定振幅の周期を抽出します。
“周期”カウントを理解するために、時間信号に対する応力-ひずみの変化と捉える方法があります。周期カウントでは、応力-ひずみヒステリシスループの数をカウントし、その範囲や平均値または最大値 / 最小値を追跡します。
レインフロー周期カウントは、最も広く使用されている周期カウント方法です。この方法では、応力の時間履歴をピークとバレーの集合に変換し、最高のピークまたは最低のバレー(絶対値が大きい方)から始まるように履歴を再編成する必要があります。つづいて、連続する3つの応力点(1、2、および3)で2つの連続する範囲を
および
として定義します。点1から点2までの周期は、
の場合にのみ抽出されます。周期を抽出すると、その周期を構成する2点は破棄され、残った各点が相互に接続されます。データ点をすべて使い切るまで、この手順が繰り返されます。次に、例を使用してSimSolidのレインフロー周期カウントのプロセスを説明します。
簡潔な荷重履歴を使用した例
次の荷重履歴があるとします。
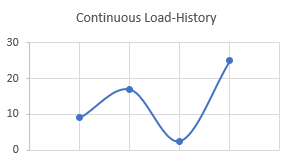
図 1.
この履歴は連続的なので、ピークとバレーのみで構成する荷重履歴に変換されます。
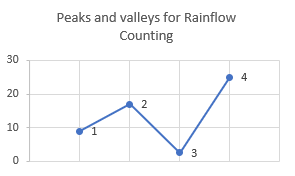
図 2.
1、2、3、4は2つのピークと2つのバレーです。点4は、この荷重履歴でのピーク応力なので、再配置によって
図 3のように先頭へ移動します。再配置の後、ピークとバレーの番号が割り当て直されます。
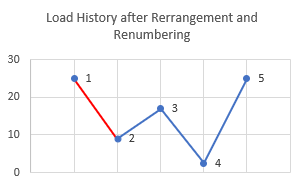 図 3.
図 3.
次に、先頭の3つの応力値(1、2、および3)に注目して、周期が存在するかどうかを判断します。
が応力値を表している場合は、以下のようになります。
なので、点1から点2の間では周期が抽出されません。ここで、次のように以降の3点を検討します。
なので、点2から点3の間で周期が抽出されます。周期が抽出されたので、この2点をグラフから削除します。
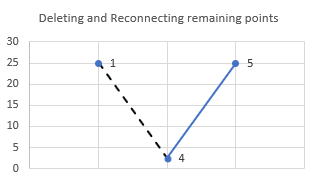
図 4.
残りの点に同じプロセスを適用します。
この場合、
なので、点1から点4の間で別の周期が抽出されます。これらの2点は破棄されます。ほかに5点が残っているので、レインフローカウントのプロセスが継続します。
この荷重履歴から、2つの周期(2→3、1→4)が抽出されています。最大のピークまたはバレーを選択して荷重履歴を再編成する主な理由のひとつは、必ず最大の周期(この場合は1→4)が抽出されるようにすることです。再配置前に荷重履歴を確認し、そのまま同じレインフローカウントプロセスを実行しても、1→4の周期は抽出されません。
より複雑な荷重履歴を使用した例
荷重履歴点の数に関係なく、レインフローカウントプロセスは同じです。ただし、再配置に使用する最大のピークまたはバレーの位置によっては、再配置プロセスがどのように実行されるかが明らかではないことがあります。次の例は、より複雑な荷重履歴の再配置プロセスを示しています。続いて実行されるレインフローカウントは、上記の簡潔な例で取り上げたプロセスの外挿にすぎず、ここでは繰り返されません。
次の過重負荷があるとします。
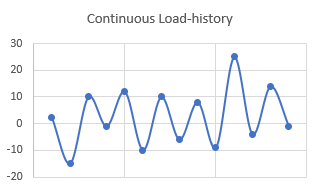
図 5.
この荷重履歴は連続的なので、次のように、ピークとバレーのみで構成する荷重履歴に変換されます。
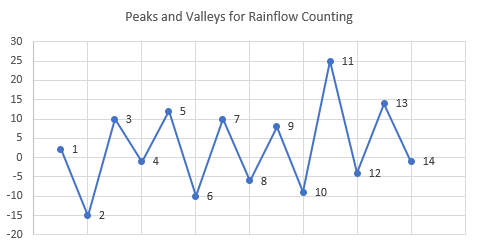
図 6.
荷重点11が最大値の荷重なので、これに基づいて荷重履歴が再編成され、番号が割り当て直されます。
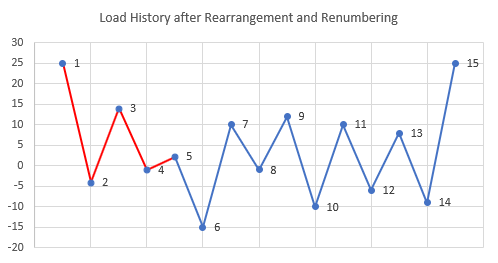
図 7.
荷重履歴が再編成されるので、最大負荷とそれに続くすべての点が荷重履歴の先頭付近に移動し、荷重履歴の末尾から削除されます。


 図 3.
図 3. 


