平均応力補正を使用して、平均応力がゼロではない場合にその効果を考慮します。
一般的には、全面的に反転した繰り返し荷重による標準的な実験から疲労曲線が得られます。しかし、実際の疲労荷重を全面的に反転することはできず、法線方向平均応力がコンポーネントの疲労性能に大きく影響します。疲労強度に対しては、引張法線方向平均応力は不利に働き、圧縮法線方向平均応力は有利に働きます。平均応力がゼロではない場合にその効果を考慮するには、平均応力補正を使用します。
材料、応力状態、環境、ひずみ振幅に応じて、通常はせん断平面または引張平面に沿った微小亀裂成長が支配的になって疲労寿命が決まります。臨界平面の平均応力補正法では、どちらのタイプの亀裂成長も左右する支配的パラメータを使用します。考えられる破壊モードとせん断や引張の支配的因子はさまざまです。したがって、寿命のすべての期間ですべての材料について、テストデータとの相関が単一の平均応力補正法で得られることを期待すべきではありません。多軸疲労寿命の予測に使用できる最良の手法は何であるかについて、一致した見解はありません。応力に基づく平均応力補正法では、引張亀裂にGoodmanモデルとFKMモデルを使用できます。せん断亀裂にはFindleyモデルを使用できます。ひずみに基づく平均応力補正法では、引張亀裂にMorrowモデルとSmith-Watson-Topperモデルを使用できます。せん断亀裂には、Brown-MillerモデルとFatemi-Socieモデルを使用できます。複数のモデルを定義すると、可能なすべての損傷値から最大の損傷が得られるモデルがSimSolidによって選択されます。
Goodmanモデル
臨界平面で引張亀裂成長の原因となる損傷を評価するにはGoodmanモデルを使用します。
(1)
各値の意味は次のとおりです:
-
: 次の式で求められる平均応力:
-
: 応力振幅
-
: 平均応力補正後の応力振幅
-
: 最終的な強度
Goodman法では、平均応力によって必ず疲労破壊が促進されるように正の平均応力補正が扱われます。一方で負の平均応力は無視されます。この方法では、圧縮平均応力に対しては控え目な結果が得られます。
破壊に至るまでのサイクル数を指定して、応力振幅と平均応力のさまざまな組み合わせによって得られる特性を記述する方法としてHaigh線図があります。
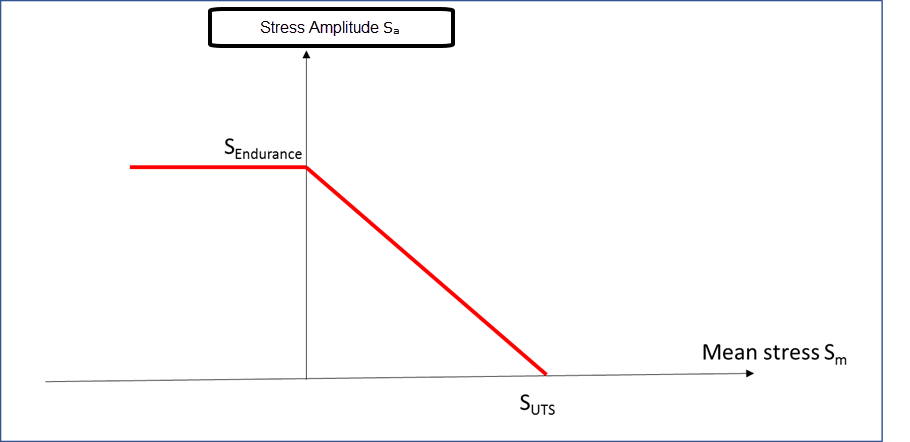
図 1. Goodman Haigh線図
Findleyモデル
寿命がきわめて長い疲労には、Findley基準を適用することが普通です。各平面の式は次のようになります。
(2)
各値の意味は次のとおりです:
: 以下の式を使用してせん断疲労強度係数
から計算する値
(3)
多くの場合、補正係数
の設定値は1.04ほどです。
注:
は、振幅に基づいて定義する必要があります。
を定義しない場合は、
SimSolidにより、次の式を使用してこの値が計算されます。
(4)(30)
定数kは、2つ以上の応力状態を扱う疲労テストを実行することによって実験的に求めます。延性材料では、多くの場合、kは0.2~0.3の範囲になります。
FKM
FKMのガイドラインに従い、応力比(R=Smin/Smax)の値を基準としてHaigh線図を4つの期間に分割します。次に補正値を使用して、損傷と寿命の計算段階で使用するSN曲線を選択します。
次に示すFKMの式は、補正済み応力振幅(
)の計算方法を示しています。損傷の計算で実際に使用する応力値は、補正済み応力振幅(
)です。入力したSN曲線にこれらの式を適用します。
期間1(R>1.0)
期間2(-∞≤R≤0.0)
期間3(0.0<R<0.5)
期間4(R≥0.5)
は平均応力補正後の応力振幅(耐久応力)、
は平均応力、
は応力振幅、Mは平均応力感度です。
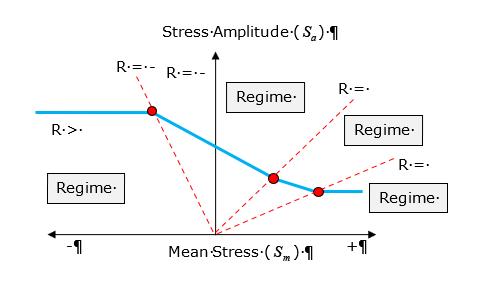
図 2.
Morrow
Morrowは、次の式によって疲労強度係数に平均応力
を導入することによって、平均応力の効果を初めて検討しました。
(5)
したがって、疲労寿命の式全体は次のようになります。
(6)
塑性ひずみが小さいときは平均応力の効果が顕著で、塑性ひずみが大きいときはその効果がほとんどなくなるという観測事実にMorrowの式は一致しています。
MORROW2:負の平均応力を無視することで、Morrow法を改良しています。
Smith-Watson-Topper
Smith、Watson、Topperは、1回の繰り返しで発生する最大応力を検討することによって平均応力を考慮する別の手法を提唱しました(わかりやすいように、以降はこの手法をSWT法と呼びます)。この場合、損傷パラメータは、1回の繰り返しで発生する最大応力とそのときのひずみ振幅の積に変更されます。
(7)
SWT法では、最大応力がゼロまたは負数となる状況は現実と一致しないので、その場合は損傷が発生しないと予測します。
これら2種類の手法を比較すると、SWT法では、引張が支配的な荷重で寿命の予測が控え目になり、Morrow法では、圧縮が支配的な荷重でより現実的な結果が得られます。
Fatemi-Socie
このモデルはせん断亀裂成長で使用します。せん断荷重がある状態では、不規則な形状の亀裂サーフェスに摩擦力が発生し、この摩擦力によって亀裂端応力が減少します。その結果、亀裂成長が抑制され、疲労寿命が長くなります。引張応力と引張ひずみによって亀裂サーフェスが分離し、摩擦力が減少します。この挙動については破断面診断による証拠が得られています。ねじりのみで破壊に至った試験片の破壊面写真では、広い範囲に摩擦が見られ、引張テストによる破壊面とは対照的に比較的特徴に乏しい破壊面になります。引張による破壊では、破壊面に個々のすべり線が確認できます。
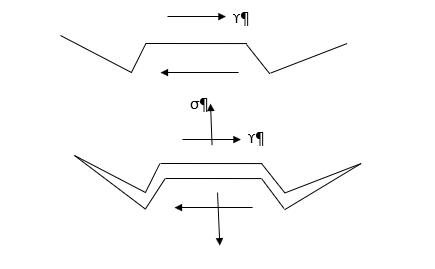
図 3. Fatemi-Socieモデル
最大応力の効果を示すために、6つの引張ねじり荷重を使用したテストを実施しています。これらの荷重は、最大せん断ひずみ振幅が同じになるように考えられています。この6つの荷重履歴すべてで、繰り返し法線ひずみも同一の一定値です。この実験では、最大せん断ひずみ振幅、相当応力振幅、相当ひずみ振幅、塑性挙動にほぼ同じ結果が得られています。これらの荷重履歴どうしの最も大きな相違点は、最大せん断ひずみが発生する平面各所の法線応力です。
各亀裂成長曲線の先頭にある図に、荷重履歴と法線応力を示します。最大応力が大きいほど、亀裂成長速度が速くなり、疲労寿命が短くなります。この材料の小さめの粒状サイズに相当する10 mmオーダーの亀裂発生を亀裂の開始とすると、亀裂の開始に対する最大応力の寄与は少なくなっています。
これらの観測事実から次のモデルが導かれます。このモデルは、亀裂の閉鎖効果を伴う法線応力によって変更した繰り返しせん断ひずみと解釈できます。
(8)
法線応力に対する材料の感度は、値
に反映されます。
は、SimSolidで有意な総ひずみとして0.002が使用される場合の応力です。複数の応力状態によるテストデータが存在しない場合はk=0.3です。このモデルは、引張荷重とねじり荷重の相違を説明するだけではなく、平均応力と非比例硬化効果の記述にも使用できます。ひずみ項のみを扱う臨界平面モデルでは、硬化に依存する平均応力やひずみ経路の効果を反映できません。
弾性ひずみと塑性ひずみは疲労損傷に等しく寄与するので、遷移寿命である2Ntが選択されます。この値は単軸疲労定数から求めることができます。
(9)
Fatemi-Socieモデルを使用してせん断ひずみ定数を求めます。
(10)
まず、せん断と引張で指数を同じにする必要がある点に注意します。
(11)
せん断係数は、引張係数から直接計算します。
(12)
単軸繰り返し応力ひずみ曲線から降伏強度を推定できます。
(13)
法線応力と法線ひずみは、遷移寿命と単軸プロパティから計算します。
(14)
(15)
(16)
弾性ポアソン比と塑性ポアソン比に適切な値を代入することで次の式が得られます。
(17)
総ひずみ結果の弾性部分と塑性部分を分離することで、せん断ひずみ寿命定数について次の式が得られます。
(18)
Brown-Miller
このモデルはせん断亀裂成長で使用します。BrownとMillerは、一定のせん断ひずみ範囲の下で引張とねじりを組み合わせたテストを実施しました。最大せん断ひずみが発生する平面の法線ひずみ範囲は、適用する引張ひずみとねじりひずみとの比率によって変化します。一定のせん断ひずみ振幅で得られた次の図のデータに基づき、BrownとMillerは、疲労プロセスの記述には2つのひずみパラメータが必要であると結論付けています。せん断ひずみと法線ひずみを組み合わせた作用によって疲労寿命が短くなるからです。
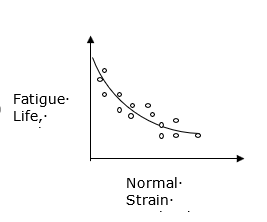
図 4. 疲労寿命と法線ひずみ振幅との関係
法線ひずみ振幅による影響
高サイクル疲労についてFindleyが提唱したせん断応力と法線応力の関係のように、BrownとMillerは、最大せん断が発生する平面では繰り返しせん断ひずみと法線ひずみの両方を考慮する必要があることを提唱しました。繰り返しせん断ひずみによって亀裂の発生が促され、法線ひずみによってその成長が促されます。両氏は、この理論を記述する次の簡潔な定式を提唱しています。
(19)
各値の意味は次のとおりです:
は相当せん断ひずみ範囲、Sは材料依存パラメータで、材料の微小亀裂成長に対する法線ひずみの影響を表現し、軸データとねじりデータの相関によって求める値です。
は最大せん断ひずみ範囲として取得され、
は、せん断ひずみ範囲
が発生する平面の法線ひずみ範囲です。適切なポアソン比を指定して弾性ひずみと塑性ひずみを別々に検討することで次の式が得られます。
(20)
各値の意味は次のとおりです:
A=1.3+0.7S
B=1.5+0.5S
疲労強度係数から平均応力を減算するMorrowの平均応力法を使用して、平均応力による効果を考慮します。最大せん断ひずみ振幅
が発生する平面上の平均応力は、軸方向平均応力の1/2となり、次の式が得られます。
(21)



