AS Card
The AS card defines an excitation by means of impressed spherical modes which are either radiating (propagating in positive r direction to infinity, with r being the radius in a spherical coordinate system) or incident onto a structure (propagating towards the origin r = 0).
On the Source/Load tab, in the Equivalent
sources group, click the ![]() Spherical modes (AS) icon.
Spherical modes (AS) icon.
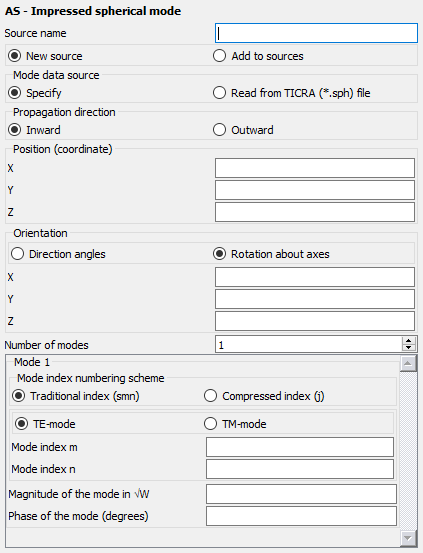
Figure 1. The AS card - Impressed spherical mode dialog.
This excitation option can thus be used for both the synthesis of an arbitrary electromagnetic field (sum of the modes weighted with complex mode coefficients), and also for the determination of the response (induced voltage or power at a load) of a receiving antenna due to the incident modes (leading to the so-called generalised scattering matrix).
Parameters:
- New source
- A new excitation is defined which replaces all previously defined excitations.
- Add to sources
- A new excitation is defined which is added to the previously defined excitations.
- Propagation direction
- Inward
- The spherical waves propagate inward. The model is illuminated with modes propagating towards r = 0 (spherical Hankel function of the first kind zn(3)= hn(1))
- Outward
- The spherical wave propagate outward. The modes radiate towards r = ∞ (spherical Hankel function of the second kind zn(4) = hn(2)).
- Mode data source
- The spherical modes can be entered directly in the .pre file or it can be imported from a TICRA file
(.sph) file. Note: Multiple spherical modes can be created as a single source.When importing from a TICRA file, the imported spherical modes may be scaled and the phase given an offset by entering values for the Magnitude scale factor and Offset phase (deg) by fields.
- Position (coordinate)
- The coordinates of the origin r = 0 of the mode in m. These values are optionally scaled by the SF card.
- angle
- The angle between the spherical mode axis (N) and the Z axis in degrees.
- angle
- The angle between the projection of the spherical mode axis (N) onto the plane Z=0 and the X axis in degrees.
- Rotation about axes
- The rotation of the spherical mode source about the X axis, Y axis and Z axis.
- Number of modes
- The number of modes that are entered in the.pre file must be specified.
- Traditional index (smn)
- If this option is checked, you can specify TE-mode (s = 1) or TM-mode (s = 2) and the indices m and n in the group below. Here n is the mode index in radial direction and must be in the range 1,2,...∞ and m is the mode index in the azimuth direction . We do not distinguish between even and odd modes (with cos(m ) and sin(m ) angular dependencies), but rather use the angular dependency . Thus the index m can also be negative, but it must be in the range −n...n.
- Compressed index (j)
- With this option, a compressed one-dimensional mode numbering scheme is used. The
Mode index j is then specified in the field below.
Here where s = 1 for TE-modes and s = 2 for TM-modes. This unified mode numbering scheme allows the computation of an extended scattering matrix (with network and radiation ports). This index j then represents a unique port number in the scattering matrix.
(1) - Magnitude of the mode in
- Absolute value of the complex amplitude of this specific spherical mode (due to the applied normalisation of the spherical modes, the unit of this amplitude is = ).
- Phase of the mode (degrees)
- The phase of the complex amplitude of this spherical mode in degrees.
- Use all data blocks
- Import all data blocks from the specified TICRA (.sph) file. The data is interpolated for use at the operating frequency.
- Use only specified data block number
- Use the data from the nth frequency block in the TICRA (.sph) file.
The implementation of the spherical modes at the AS card follows closely the references:
J. E. Hansen, Spherical Near-field Antenna Measurements, Peter Peregrinus Ltd., London, 1988 and B. C. Brock, Using Vector Spherical Harmonics to Compute Antenna Mutual Impedance from Measured or Computed Fields, Sandia National Laboratories, Report SAND2000-2217-Revised, April 2001. One must realise that Hansen assumes a complex time dependence of , while Feko always uses the positive sign .
In Feko, using the modal coefficients the electric and magnetic field strength is represented in a spherical coordinate system by
Here s, m and n are the mode indices with s = 1 indicating the TE-mode and s = 2 the TM-mode, and c represents the propagation direction: c = 3 is inward and c = 4 is outward. The term ZF denotes the wave impedance of the medium under consideration, below is the corresponding wavenumber.
The spherical wave functions are given by
It should be noted that the Legendre polynomial as used in Feko follows the definitions of Abramowitz / Stegun (also used like this in Numerical Recipes) or also Harrington. The formulas used in other references (for example, Stratton or Hansen) have an extra factor (−1) m included. This is not considered in Feko, and thus the mode coefficients might differ from those computed according to Hansen (there is also of course the other time dependency).
Theoretically the index n runs in the range 1,2,...,∞. For any practical application, one will have to consider a finite number of modes only, limit the range n = 1...N. A few rules of thumb exist for the selection of N. For instance when representing the pattern of an antenna by spherical modes one can use the upper limit
for j (j = 1...J then). So for instance for an antenna with enclosing radius r0 = (then = 1.57) when using the last of the three rules of thumb above, one would need roughly N ≈ 5 or J ≈ 70 modes, respectively. For r0 = these limits become already N ≈ 12 and J ≈ 336, and for r0 = 5 one has to use N ≈ 41 and J ≈ 3526 modes The modes have been normalised such that each mode has a constant power flow through any spherical surface (either inwards or outwards). In principle one could use the PW card for this, but then power normalisation works only if there is not more than one mode active at the same time (when using the PW card, just the total radiated power of all the modes is determined, and then each mode is scaled with the same factor, so that the total radiated power is correct, but here we enforce a specified power for each individual mode). The power for each mode is independent of the mode indices
(unit is correctly Watt since the amplitude has a unit ). Since the modes are orthogonal, if multiple AS cards are active at the same time, the powers of the individual modes can just be added. Any other power corrections (such as due to metallic elements being in the vicinity) are not taken into account in Feko.
If an AS excitation is used in connection with multiple different media, it should be noted that we assume outward propagating modes (when Outward is selected) to originate from the source position. The source is located in the medium where its position is specified, and its contribution will be zero in all other media.
For inward propagating modes (when Inward is selected) we assume the propagating modes to originate at infinity, in the free space medium 0, and such modes only contribute to this medium with index 0. In connection with the UTD, only outward propagating modes are allowed (they have a well defined source point), while inward propagating modes are not supported (neither a source point nor an incidence direction can be assigned to such modes).
- Induced voltage or power at the antenna terminals for the network ports (no far field computation).
- Field scattered back, and decomposition of this field into spherical modes (far field ports). Here one needs the far field computation, but similar to an RCS computation with an incident plane wave, only the scattered far field is of interest, which can be obtained from the FF card without problems.
** Create the far-field radiation pattern of a spherical mode
** No geometry
EG: 1 : 0 : 0 : : : : : : : : : : 1
** Set the frequency
FR: 1 : 0 : : : : 100e6
** Spherical mode indices
#s=1 ** 1 = TE-mode, 2 = TM-mode
#n=5 ** mode order n (with n=1, 2, 3, ...)
#m = 0 ** mode order m (with m=-n ... n)
** Excitation
AS: 0 : 4 : #s : #m : #n : 1 : 0
** Compute the full far-field pattern
FF: 1 : 91 : 37 : 0 : 0 : 0 : 0 : 2 : 10 : : : 0
** End
ENThe resulting pattern is shown in Figure 2. From the Feko output file one can see the correct radiated power of 0.5 Watt as obtained from the far field integration:
Integration of the normal component of the Poynting vector in the angular
grid DTHETA = 2.00 deg. and DPHI = 10.00 deg. ( 3367 sample points)
angular range THETA angular range PHI radiated power
-1.00 .. 181.00 deg. -5.00 .. 365.00 deg. 5.13889E-01 Watt
0.00 .. 180.00 deg. 0.00 .. 360.00 deg. 5.00001E-01 Watt
Figure 2. The 3D radiation pattern of a spherical TE-mode with n=5 and m=0.