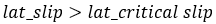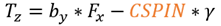Force Calculation
Vertical Force

Figure 1. Front view of tire at an inclination angle
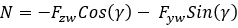
Where 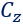 is the vertical stiffness of the tire. The lateral deflection is
ignored in the calculation.
is the vertical stiffness of the tire. The lateral deflection is
ignored in the calculation.
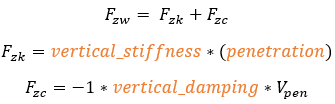
Where 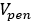 is the tire penetration velocity.
is the tire penetration velocity.
The vertical force can only be positive: in the case of a lift off condition of the tire from the ground, the resulting negative reaction force is set to 0.
If a [DEFLECTION_LOAD_CURVE] block is present in tire property file, then the data inside the block is used to calculate the vertical force. In this case the VERTICAL_STIFFNESS value is ignored. The data in DEFLECTION_LOAD_CURVE should be monotonically increasing. An example of such table is given below:

Friction Coefficient
The friction coefficient can be calculated in three ways:- Interpolating the Umax and Umin value using Comprehensive slip.
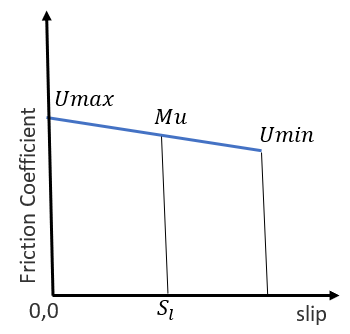
Figure 2. Friction Coefficient versus Slip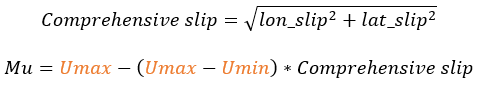
- Interpolating Mu using Vertical Force from a table.
- Interpolating Mu using Slip from a table.
Option 1 is the default option. Option 2 or 3 can be used when you have a table representing Mu versus Vertical Force or Mu versus Slip as shown below:

Figure 3.
In such a case, the parameter Mu must be set accordingly to the name of the block containing this table in the [parameter] block.
The table data must be provided within a block in the property file as shown below:
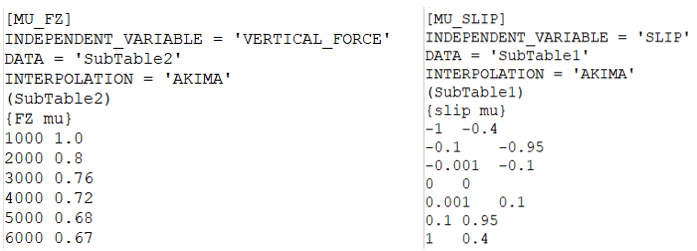
Figure 4. Block Containing Mu versus Fz and Mu versus Slip
| INDEPENDENT_VARIABLE | The friction coefficient is a function of this variable. There are two options: VERTICAL_FORCE and SLIP. |
| DATA | The sub table within this block containing the table data. |
| INTERPOLATION | Scheme used for interpolating the curve. There are four options: LINEAR, CUBIC, AKIMA, QUINTIC. Default = AKIMA. |
To continue supporting previous versions, if the block [MU_SLIP_CURVE] is specified, it will be used without setting the Mu parameter block (MU_FZ or MU_SLIP). In such a case, the friction coefficient is calculated by interpolating the data in the table of the block [MU_SLIP_CURVE].
The data in [MU_SLIP] curve should be monotonically increasing. An example table is shown below:

Longitudinal Force
The calculation of the longitudinal force (Fx) depends on the longitudinal slip condition of the tire. Typically, there are two distinct slip states: an elastic deformation state (where the longitudinal slip is less that a critical slip value) and a pure sliding state (where the longitudinal slip exceeds the critical slip value).The critical longitudinal slip is calculated below:

In case of pure elastic deformation 
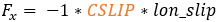
In case of pure sliding 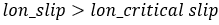
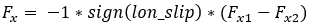
Where:
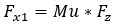
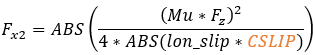
Lateral Force
Similar to the critical slip for longitudinal force, a critical lateral slip factor is calculated. It determines the boundary between pure elastic deformation conditions and pure sliding condition of the tire.

In case of elastic deformation state 
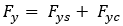
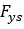 and
and 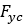 are the lateral forces due to later slip and camber
respectively.
are the lateral forces due to later slip and camber
respectively.

 is the camber angle, when
is the camber angle, when 

And if  >
> 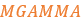
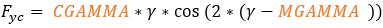
Where:

In case of sliding 

Overturning Moment
An overturning moment is caused by the shift of the contact point (at which the vertical force is applied) in the lateral direction.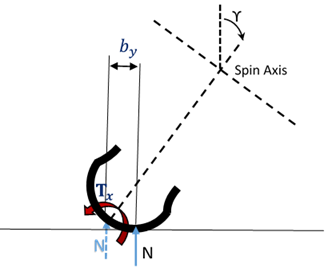
Figure 5. Overturning Moment at the inclination angle

Rolling Resistance Moment
In the FIALA tire model the rolling resistance moment is purely a function of the normal force Fz:
Where omega is angular velocity of tire about spin axis.
Aligning Torque
The same critical lateral slip used in the Fy calculation is also used in determining the condition of the tire.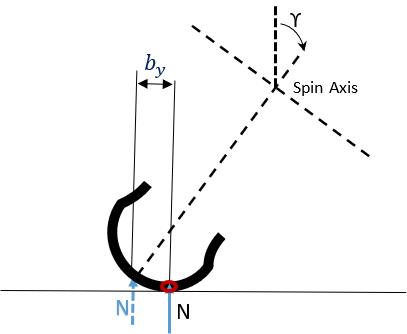
Figure 6. Point of action longitudinal force which creates a moment about the vertical axis
In case of elastic deformation state 
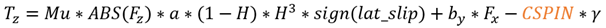
Where 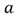 is half of the contact patch length. The scaling factor here is half of the contact patch
length, however in a FIALA model; the tire width is used as a scaling factor.
is half of the contact patch length. The scaling factor here is half of the contact patch
length, however in a FIALA model; the tire width is used as a scaling factor.
In case
of sliding