Simple Averaging
Simple averaging means that tensor and vector components are extracted, and the invariants are computed prior to averaging.
For example, as shown in the Nodal Averaging of Elemental Results topic, there are four tensors, [A2], [B1], [C3], and [D4] at four corners at Node 400.
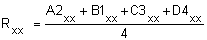
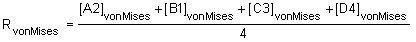
Absolute max principal is a special case. The principals P1, P2, P3 are first averaged to the node, and then absolute max principal is computed from these three averaged values.
| Element Type | Reference System | Projection Rule | Description |
|---|---|---|---|
| Solid | Global | N/A | All corresponding tensors and vectors are transformed to the global coordinate system and then a component or invariant is averaged as explained above. |
| Analysis | N/A | All corresponding tensors and vectors are left in their original coordinate system (no transformation occurs) and then a component or invariant is averaged as explained above. In this case, each participating element result can be in a different system. Simple averaging for components ignores variations in systems. Since invariance does not depend on the coordinate system, all reference systems will produce the same results for invariants. | |
| Elemental | N/A | All corresponding tensors and vectors are transformed to the elemental coordinate system and then a component or invariant is averaged as explained above. In this case, each participating element result can also be in a different system. Simple averaging for components ignores variations in systems. Since invariance does not depend on the coordinate system, all reference systems will produce the same results for invariants. | |
| User-defined | N/A | All corresponding tensors and vectors are transformed to the user-defined coordinate system and then a component or invariant is averaged as explained above. | |
| Shell | Global | ON | All corresponding tensors and vectors are transformed to the projected system
(following the projection rule) of the participating elements and then the
component or invariants are averaged as explained above. As a result, even if the reference system is the same, the projected systems in participating elements can be different. Simple averaging for components ignores variations in systems. |
| OFF | All corresponding tensors and vectors are transformed to the global coordinate system and a component or invariant is then averaged as explained above. | ||
| Analysis | N/A | All corresponding tensors and vectors are left in their original coordinate system (no transformation occurs) and then a component or invariant is averaged as explained above. In this case, each participating element result could be in a different system. Simple averaging for components ignores variations in systems. Since invariance does not depend on the coordinate system, all reference systems will produce the same results for invariants. | |
| Elemental | N/A | All corresponding tensors and vectors are transformed to the elemental coordinate system and then a component or invariant is averaged as explained above. In this case, each participating element result could also be in a different system. Simple averaging for components ignores variations in systems. Since invariance does not depend on the coordinate system, all reference systems will produce the same results for invariants. | |
| User-defined | ON | All corresponding tensors and vectors are transformed to the projected system
(following the projection rule) of the participating elements and then the
component or invariants are averaged as explained above. As a result, even if the reference system is the same the projected systems in participating elements can be different. Simple averaging for components ignores variations in systems. |
|
| OFF | All corresponding tensors and vectors are transformed to the User-defined coordinate system and a component or invariant is then averaged as explained above. |
Valid reference coordinate system: All (Global, Analysis, Elemental, and User-defined)