/FAIL/GURSON

Block Format Keyword A Gurson-Nahshon-Hutchinson failure model describing the damage in terms of void nucleation and growth in metal plasticity.

The modified Gurson formulation adds additional damage accumulation terms for shear dominated loads, specific treatment under compressive loading, and elastic stiffness loss with damage.

Format

(1)	(3)	(5)	(10)
/FAIL/GURSON/`mat_ID`/`unit_ID`
$q_{1}$	$q_{2}$		`I`_loc
$ε_{n}$	`A`_s	`K`_w
$f_{c}$	$f_{F}$	$f_{I}$
`R`_len	`H`_chi	$L_{e}^{M A X}$

Optional line

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`fail_ID`

Definition

Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	(Optional) Unit Identifier. (Integer, maximum 10 digits)
$q_{1}$	First Gurson damage coefficient. Default = 1.5 (Real)
$q_{2}$	Second Gurson damage coefficient, maximum value = 1.02. Default = 1.0 (Real)
`I`_loc	Damage variable accumulation method flag. = 0 Set to 1. = 1 (Default) Local damage formulation. = 2 Non-local damage regularization using the Micromorphic method. = 3 Non-local damage regularization using the Peerlings method. (Integer)
$ε_{n}$	Equivalent plastic strain at void nucleation. (Real)
`A`_s	Linear void nucleation slope. (Real)
`K`_w	Shear damage growth coefficient. (Real)
$f_{c}$	Critical void volume fraction at void coalescence. (Real)
$f_{F}$	Void volume fraction at ductile failure. (Real)
$f_{I}$	Initial void volume fraction. (Real)
`R`_len	Radius of non-local variable influence (`I`_loc > 1). (Real)	$[m]$
`H`_chi	Non-local penalty parameter (Micromorphic method only, `I`_loc = 2). (Real)	$[Pa]$
$L_{e}^{M A X}$	Mesh convergence element length target. 5 (Real)	$[m]$
`fail_ID`	(Optional) Failure criteria identifier. (Integer, maximum 10 digits)

Comments

The Gurson damage model may only be used with the elasto-plastic material /MAT/LAW104. The yield surface definition of the material law is modified by adding the damage evolution terms: (1)
$ϕ = \frac{σ_{e q}^{2}}{σ_{y l d}^{2}} - 1 + 2 q_{1} f^{*} c o s h (\frac{η_{t} q_{2} T r (σ)}{2 σ_{y l d}}) - {(q_{1} f^{*})}^{2} = 0$

Where,

$q_{1}$ , $q_{2}$

Two Gurson-Tveergard-Needleman parameters.

$f^{*}$

Effective damage

$η_{t}$

Factor defined as:

$η_{t} = {\begin{cases} 0, f_{t} = 0 and T r (σ) < 0 \\ 1, otherwise \end{cases}$

$f_{t}$

Total void volume fraction that is computed incrementally.

$d f_{t} = d f_{n} + d f_{g} + d f_{s h}$
The kinetic equations of the damage factor increments are:
- Void nucleation (creation of microcavities), decreasing at low triaxiality.(2)
  $d f_{n} = {\begin{matrix} A_{s} d ε_{p}, ε_{p} \geq ε_{n} and τ \geq 0 \\ A_{s} (1 + 3 τ) d ε_{p}, ε_{p} \geq ε_{n} and - \frac{1}{3} \leq τ < 0 \\ 0, ε_{p} < ε_{n} and τ < - \frac{1}{3} \end{matrix}$
  
  Where, $τ$ is the stress triaxiality defined as:(3)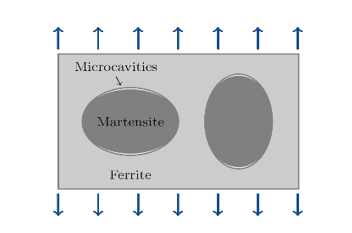
  $τ = \frac{T r (σ)}{3 σ_{e q}}$
  
  Figure 1. Nucleation of cavities
- Void growth at high triaxiality:(4)
  $d f_{g} = (1 - f_{t}) T r (ε_{p})$
  
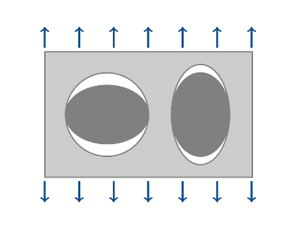
  Figure 2. Growth of cavities at high triaxiality
- Additional shear void growth at low triaxiality which is shear dominated: (5)
  $d f_{s h} = K_{w} f_{t} w (θ) \frac{S : ε_{p}}{σ_{e q}}$
  
  Where, $w (θ)$ is a weight function depending on the Lode angle: (6)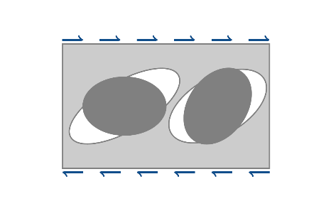
  $w (θ) = 1 - {(cos (3 θ))}^{2}$
  
  Figure 3. Growth of cavities at low triaxiality
  
  To represent the cavities coalescence when a critical void volume fraction $f_{c}$ is reached by $f_{t}$ , the effective damage (which has an influence on the stress computation) $f^{*}$ is introduced in the model and its expression depends on $f_{t}$ : (7)
  $f^{*} = f (f_{t}) = {\begin{matrix} f_{t}, f_{t} < f_{c} \\ f_{c} + (\frac{1}{q_{1}} - f_{c}) \frac{(f_{t} - f_{c})}{(f_{R} - f_{c})}, f_{t} \geq f_{c} \end{matrix}$
  
  Where, $f_{R}$ is the total void volume fraction at rupture for which 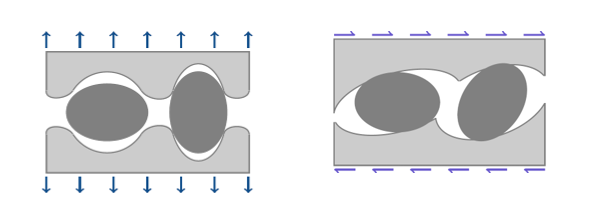$f^{*} = 1 / q_{1}$ .
  
  Figure 4. Coalescence of cavities
  
  To take into account the effect of the stiffness loss, a damage variable $D$ is computed as: (8)
  $D = q_{1} f^{*}$
  
  The effective damage $f^{*}$ is normalized by its rupture value $1 / q_{1}$ which gives $0 \leq D \leq 1$ . The stress tensor is then computed as: (9)
  $σ = (1 - D) \tilde{C} ε_{e}$
  
  Where, $\tilde{C}$ is the elastic stiffness matrix.
  
  The material fails when the cumulated total damage factor reaches the limit value $f_{R}$ . The element is then deleted.
By default $I_{l o c} = 1$ , the damage variable is calculated step by step using the local plastic strain values at each integration point. However, one may want to use non-local regularization which offers mesh size and the mesh orientation independent results (mesh convergence) for all meshes using the mesh size $L_{e}$ less than equal to the maximum value set by you $L_{e} \leq L_{e}^{m a x}$ . This maximum mesh size $L_{e}^{m a x}$ is then the highest mesh size used for which results are mesh convergent.
If one of the non-local formulations is used, $(I_{l o c} > 1)$ , the damage increments depend on a regularized nodal “non-local” plastic strain calculated on the entire mesh. The non-local plastic strain at nodes denoted $ε_{p}^{n l}$ is computed accounting for its own gradient and its local counterpart $ε_{p}$ computed at the Gauss points following the set of equations: (10)
$\begin{matrix} R_{l e n}^{2} Δ ε_{p}^{n l} - γ \dot{ε_{p}^{n l}} + (ε_{p} - ε_{p}^{n l}) = ζ \ddot{ε_{p}^{n l}} \\ \vec{\nabla} ε_{p}^{n l} . \vec{n} = 0 \end{matrix} \begin{matrix} o n \\ o n \end{matrix} \begin{matrix} Ω \\ Γ \end{matrix}$

The parameters $γ$ and $ζ$ are automatically set. You have to set the parameter R_len (or $L_{e}^{M A X}$ - Comment 5) which defines a non-local “internal length” which corresponds to a radius of influence in the non-local variable computation. This defines the size of the non-local regularization band $L_{r} = f (R_{l e n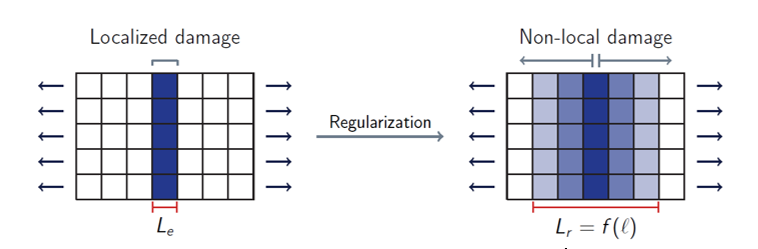})$ (Figure 5).

Figure 5. Non-local regularization principle

To help choose a value for the parameter R_len, one may follow the following expression:(11)
$R_{l e n} \approx \frac{3 L_{e}^{m a x}}{\sqrt{π}}$
If $I_{l o c} = 2$ , the non-local Micromorphic method will be used. For this method, the parameter is required, H_chi. This parameter and the non-local plastic strain $ε_{p}^{n l}$ are introduced in the constitutive equation as: (12)
$R_{c h i} (ε_{p}, ε_{p}^{n l}) = R (ε_{p}) - H_{c h i} (ε_{p}^{n l} - ε_{p})$

Where, $R (ε_{p})$ is the classical work-hardening function. This newly defined micromorphic work-hardening function R_chi is introduced in the flow stress computation $σ_{y l d}$ . The parameter H_chi becomes a penalty parameter and if $H_{c h i} \to \infty$ , then $ε_{p} \to ε_{p}^{n l}$ and $ε_{p}^{n l} \to ε_{p}$ and so $ε_{p} \approx ε_{p}^{n l}$ . This method is thermo-dynamically well defined. However, it is hard to identify the input values and it changes the plastic behavior of the model. This is why it is recommended to use the Peerlings method $I_{l o c} = 3$ .
If $I_{l o c} = 3$ , the non-local Peerlings method will be used. For this method, the parameter H_chi is used. Only the non-local length R_len is used. This method is simpler than the Micromorphic one. It introduces the non-local plastic strain in the softening variable kinetic equation (damage and temperature if thermal effects are considered): (13)
${\dot{f}}_{t} = \underset{Void nucleation}{\underset{︸}{A \dot{ε_{p}^{n l}}}} + \underset{\begin{matrix} Void growth \\ (high triaxiality) \end{matrix}}{\underset{︸}{(1 - f_{t}) T r (\dot{ε_{p}^{n l}})}} + \underset{\begin{array}{l} Shear nucleation \\ (low triaxility) \end{array}}{\underset{︸}{K_{w} f_{t} w (θ) \frac{S : \dot{ε_{p}^{n l}}}{σ_{e q}}}}$
(14)
$\dot{T} = ω (\dot{ε_{p}^{n l}}) \frac{η}{ρ C_{p}} \bar{\bar{σ}} : \dot{ε_{p}^{n l}}$

This method is recommended since it is simple to identify the input parameters and does not modify the plastic behavior of the material.
To set the non-local length parameter R_len, you can choose:
- Directly input the value of R_len in the input card, if a direct control on this parameter is wanted. In this case, the parameter $L_{e}^{M A X}$ must be ignored and set to none.
- Input the maximum mesh size $L_{e}^{M A X}$ for which results have reached mesh convergence. The non-local regularization will then be effective for all mesh sizes $L_{e}^{}$ such as $L_{e} \leq L_{e}^{m a x}$ . In this case R_len is calculated automatically according to the value of $L_{e}^{M A X}$ , and the input value of R_len is ignored. For instance, if you want to get converged and mesh-independent results for a mesh size of 5 mm, $L_{e}^{m a x} = 5$ mm. In this case, the results will be converged, mesh-size and mesh orientation independent for $L_{e} \leq 5$ mm.
When a non-local regularization is used for shell elements, an additional regularization is made on the thickness variation computation avoiding an additional localization issue. In the common local case (Figure 6), the compatibility of thickness between shell elements is not ensured due to the lack of kinematic equations in the z-direction, and the thickness variation is locally computed at Gauss points. By introducing the non-local plastic strain in the “in-thickness” strain increment, the compatibility is restored, (Figure 7). (15)
$Δ ε_{z z} = - \frac{ν}{1 - ν} (Δ ε_{x x} - Δ λ_{n l} n_{x x} + Δ ε_{y y} - Δ λ_{n l} n_{y y}) + Δ λ_{n l} n_{z z}$

Where, $Δ λ_{n l} = f (ε_{p}^{n l})$ is the non-local plastic multiplier.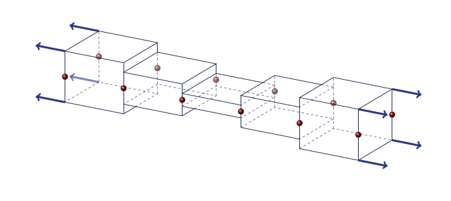

Figure 6. Transverse strain incompatibility (local)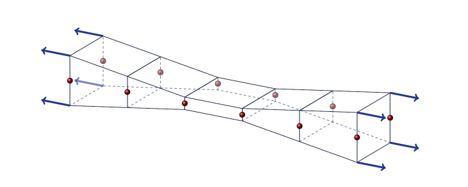

Figure 7. Transverse strain compatibility (non-local)

Note: This last point implies that the identified parameters can be used on solid and shells, as results will be identical within the same range of stress triaxiality $- \frac{2}{3} \leq η \leq \frac{2}{3}$ .
To create a specific damage output DAMA in ANIM and H3D files, the total damage is normalized by its rupture value: (16)
$D = \frac{f_{t}}{f_{R}}$