Introduction / examples
Definition
A problem is known to be of time dependent or of transient type when the state variable, respectively the unknown of the associated system, is a function of time. Two examples are presented in the following paragraphs.
1st example (thermal application)
The differential equation solved using finite element method in a Thermal Transient application is the following:
![]()
where:
- [k] is the tensor of thermal conductivity
- ρCp is the volume heat capacity
- q is the volume density of power of the heat source
- T is the temperature, respectively the state variable, i.e. the unknown of the system
In this case, the temperature T is a function of time (differential equation of first degree).
2nd example (magnetic application)
The differential equation solved using finite element method in a Transient Magnetic application (with the vector model) is the following:
![]()
where:
- [ν] is the tensor of the magnetic reluctivity in the computation domain
- [σ] is the tensor of the electric conductivity of the computation domain
-
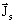 is the density of the current source
is the density of the current source -
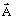 is the magnetic vector potential, respectively the
state variable, i.e. the unknown of the system
is the magnetic vector potential, respectively the
state variable, i.e. the unknown of the system
In this example, the magnetic vector potential A is function of time (differential equation is of first degree).
Time discretization equations
The method called step by step in time domain is applied for the integration of this last differential equation with respect to the time variable. The time domain is divided into smaller time intervals, called time steps, during which the linear variation of the unknown with respect to time is assumed.