計算される結果
HyperViewで計算される結果の一覧。
- 主応力と主ひずみ
- 指定された応力 / ひずみテンソルSについて、3つの主値が次の3次方程式の根として求められます:
- フォンミーゼス応力
- =
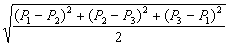
- フォンミーゼスひずみ
- =
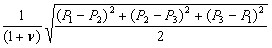
- 符号付フォンミーゼス
- 符号付フォンミーゼスの符号は、最も大きい絶対値を有する主値の符号によって決定されます。
- 圧力
- 3つの垂直応力の平均:
- 強度
- 最大主応力と最小主応力との絶対差:
- 最大せん断
- 最大せん断応力 / ひずみ:
- トレスカ
- 下記の最大値として計算されます:
- Lodeparam xi
- =
[(27/2) *(P1+pressure) * (P2+pressure) * (P3+pressure)] / (vonMises* vonMises * vonMises); - Lodeparam theta
- =
1 – [2 * Pi * arccos(lodeparamxi)]; - 軸性
- =
-pressure/VonMises - 最大主値の絶対値
- 3つの主応力またはひずみの最大の絶対項がコンター表示されます。つまり、最大主値の絶対値は3つの主応力(またはひずみ)の極大値です。
参考資料
VonMises Strain Calculation - PapersYu Yang, Wang Ningfei, ZhangPing, Three-dimensional Damage Analysis of Free Loading Solid Propellant Grains Subjected to Low Temperature Loading.School of Mechano-Electronics Engineering, Beijing Institute of Technology, Beijing 100081, China.
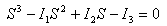
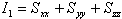
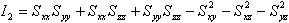
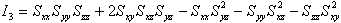
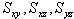 は“テンソルせん断ひずみ”フォーマットです。各種ソルバー出力せん断ひずみは、2つのフォーマット“工学せん断ひずみ”および“テンソルせん断ひずみ”のいずれかです。“工学せん断ひずみ”は“テンソルせん断ひずみ”の2倍です。フォーマットのせん断ひずみを有するすべてのソルバーデータは、主値の計算に先駆け、“テンソルせん断ひずみ”に変換されます。これには、
は“テンソルせん断ひずみ”フォーマットです。各種ソルバー出力せん断ひずみは、2つのフォーマット“工学せん断ひずみ”および“テンソルせん断ひずみ”のいずれかです。“工学せん断ひずみ”は“テンソルせん断ひずみ”の2倍です。フォーマットのせん断ひずみを有するすべてのソルバーデータは、主値の計算に先駆け、“テンソルせん断ひずみ”に変換されます。これには、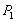 、
、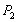 、
、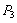 は、応力テンソルについて上記で計算される主応力を表わします。
は、応力テンソルについて上記で計算される主応力を表わします。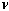 はポワソン比です(デフォルト値は
はポワソン比です(デフォルト値は