温度係数
概要
温度に依存し、指数関数的減衰を伴う、B(H)曲線用に提供されているモデルは、以下を使用して定義されます。
- 軟質材料用に提供されている以前のモデル
- 2つの指数関数に基づいたCOEF(T)温度係数(以下で詳述します)
温度係数
COEF(T)温度係数は次の2つの指数関数によって定義されます:
- 1つ目は、負の曲率を有し、この係数の範囲が1~0.1(T<T1)である場合に使用されます。
- 2つ目は、正の曲率を有し、この係数の範囲が0.1~0(T<T1)である場合に、キュリー点の付近で使用されます。
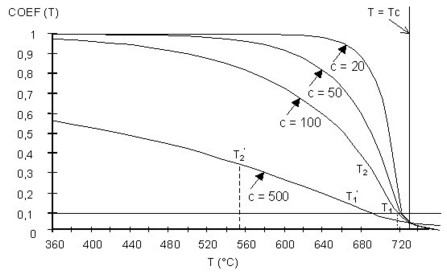
COEF(T)温度係数の形状を次の図に示します。
数学モデル
COEF(T)温度係数は次のように定義されます:
T < T1の場合:![]()
ここで、温度T1の場合、COEF1(T1) = 0.1となります。
この最後の関係は次のように記述することもできます:T1 -Tc =C ln 0.9
T > T1の場合:![]()
ここで、量T2の値は、2つの指数関数の結合がT1で成立するような値です(すなわちCOEF2(T1) = 0.1)。
この最後の条件は次のように記述することもできます:T2 -T1 =0.1C ln 0.1
ここで:
- Tcはキュリー温度°C
- Cは温度定数°C
正確な数式
1と0.1の間で上記で使用されているCOEF(T)の式は近似です。正確な式は次のとおりです:
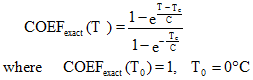
Tcが上昇すると、1000K付近では、次の近似式を使用します:
![]()
Td0 = 0°Cにおいては、次のとおりです:
![]()
例
COEF(T)関数の形状を次の図に示します。
ユーザーによって指定された温度定数Cの値に従って、COEF(T)係数の減少は多かれ少なかれ急速です。