鉄損モデル

概要

どちらの場合も、定義したモデルはポストプロセッサによる計算でのみ使用します。解析プロセスでは鉄損が考慮されません。

Fluxで鉄損モデルを使用できるのは積層領域に限られています。このモデルで使用する磁束密度は、以下のように定義した鋼板のブロック内部での均質な磁束密度です。

回転磁界が存在する場合は、曲線By = f(Bx)が楕円形状になることがあるので、均質な誘導ベクトルを次のように分解することをお勧めします。

${\mathit{B}}_{\mathit{h}}=\left[\begin{array}{c}{B}_{\backslash \backslash }\\ B_{⏊}\end{array}\right]$

この両方の軸は、図 1に示す楕円曲線の短軸と長軸に相当します。

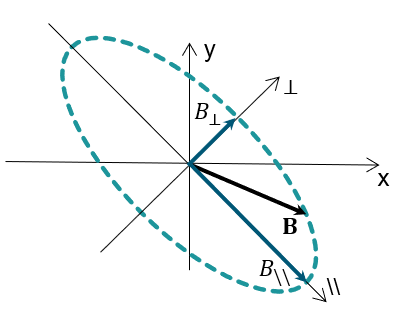
図 1. 曲線By = f(Bx)

修正Bertottiモデル

モデルの概要説明：

Bertottiの理論は、周波数と磁束密度に依存する磁気損失の式を提唱しています。

電力密度は、次の過渡磁気関係で記述できます：

$dP\left(t\right)=K_f\left(k_{1 }f{\left(\frac{∆B_{\backslash \backslash }+ ∆B_{⏊}}{K_f}\right)}^{{\alpha }_1}+k_{2 }g\left({\alpha }_2\right)\frac{1}{{K_f}^{{\alpha }_2}}{\left|\frac{d{B}_h}{dt}\right|}^{{\alpha }_2}+k_3 g\left({\alpha }_3\right)\frac{1}{{K_f}^{{\alpha }_3}}{\left|\frac{d{B}_h}{dt}\right|}^{{\alpha }_3}\right)$

$g\left({\alpha }_i\right)= \frac{2}{{\left(2\pi \right)}^{{\alpha }_i-1} 4\int {cos}^{{\alpha }_i}\left(\theta \right) d\theta }$

*追加損失 / 超過損失と従来の損失の区別は人為的です。これらの損失は1つの用語で表現でき、鋼板内部を流れる実際の誘導電流に対応します。

これらの係数と指数（修正版Bertottiモデル同定ツール）を求めることができるExcelシートが以下のパスにあります：

INSTALLATION_FOLDER\Flux\DocExamples\Tools\BertottiLossesCoefficients

ここで、INSTALLATION_FOLDERは、ご使用のシステムのFluxインストールディレクトリを表します。

修正版Bertottiモデル同定ツールを実行するには、この場所にあるBertottiLossesCoefficients.xlsというファイルをMicrosoft Excellで開きます。

妥当性の範囲

Steady State AC Magneticアプリケーションでは、電力密度を次の方程式で表現します：

$dP=\left(k_1 B_{max}^{{\alpha }_1} f+{k_2 {(B}_{max} f)}^{{\alpha }_2}+{k_3 {(B}_{max} f)}^{{\alpha }_3} \right)K_f$

このソフトウェアでは、各ポイントの磁束密度の値を使用します。したがって、Steady State AC Magneticシミュレーションでは、回転機械で表現した問題に関する結果を詳しく検討するにはこの値が効率的です。実際、このようなシミュレーションでは、固定子を基準とした回転子の位置を固定として、回転子の電気回路の導体が持つ抵抗率を変えることによって、実際の回転子の運動をモデル化しています。このように計算した磁束密度は、固定子に対して回転子が所定の位置にあるとき、その1ポイントで空間高調波に起因して最大になります。これにより、回転子が回転しているとした場合の時間ドメインでの一定期間にわたり、計算した磁束密度のピーク値が実際のピーク値に対応しない結果になります。したがって、この場合は磁気損失の計算を慎重に扱う必要があります。

さらに、磁気的挙動則B(H)を非線形近似する場合は、磁化の等価モデルを使用して導入した飽和現象によって、磁束密度の局所値が変化することが考えられます。

材料内部での修正Bertottiモデル定義の手順

LSモデル

プレゼンテーション

特性曲面H(B, dB/dt)：

材料ごとの特性曲面H(B,dB/dt)は、中間周波数での磁気測定にエプスタインタイプのデバイスを使用して取得できます。

このような曲面の例を下の図に示します。

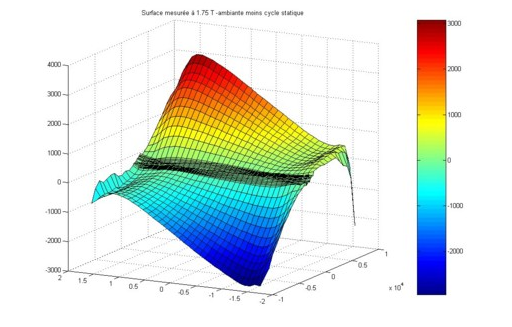
図 2. H(B, dB/dt)曲面

サイクルの再構成：

解析モデルを使用すると、Bの値から磁界強度Hを次のように再構成できます。

H(B,dB/dt) = Hstatic(B) + Hdynamic (B,dB/dt)

したがって、下図のようなB(H)曲線が得られるので、きわめて正確に鉄損を計算できます。

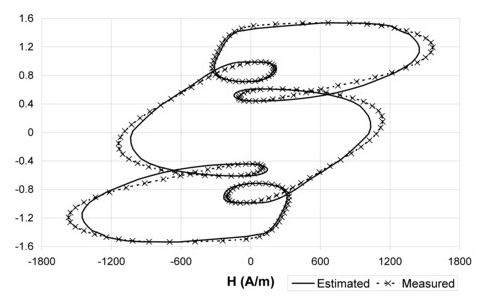
図 3. 200Hzでの正弦波磁束密度と5次高調波

LSモデルは、このような目的に特化して記述したさまざまな積層に割り当てられます。

電気鋼板の詳細については、次のページをご参照ください： 電気鋼板に関する標準

このモデルを使用して、Fluxに独自の材料をインポートすることもできます（MILSによるLSモデルの識別をご参照ください）。

材料でのLSモデルの定義

次の項をご参照ください： 等方性軟質材料：LSモデルで記述した鋼板