OS-T: 1020 Normal Modes Analysis of a Splash Shield
In this tutorial, an existing finite element model of an automotive splash shield is used to demonstrate how to set up and perform a normal modes analysis. HyperView post-processing tools are used to determine mode shapes of the model.
The sshield.fem file is needed to perform this tutorial.
Launch HyperMesh and Set the OptiStruct User Profile
Import the Model
Set Up the Model
Review Properties of Rigid Elements
To be able to distinguish the spiders clearly in the model, you will
use the Shaded Elements and Mesh Lines icon  .
.
The dependent nodes of the rigid elements have all
six degrees of freedom constrained. Therefore, each "spider" connects nodes of the
shell mesh together in such a way that they do not move with respect to one another.
Revert to the Wireframe Elements Skin Only mode by clicking on the  icon.
icon.
Create the Material
The imported model has four component collectors with no materials. A material collector needs to be created and assigned to the shell component collectors. The rigid elements do not need to be assigned a material.
Edit the Properties
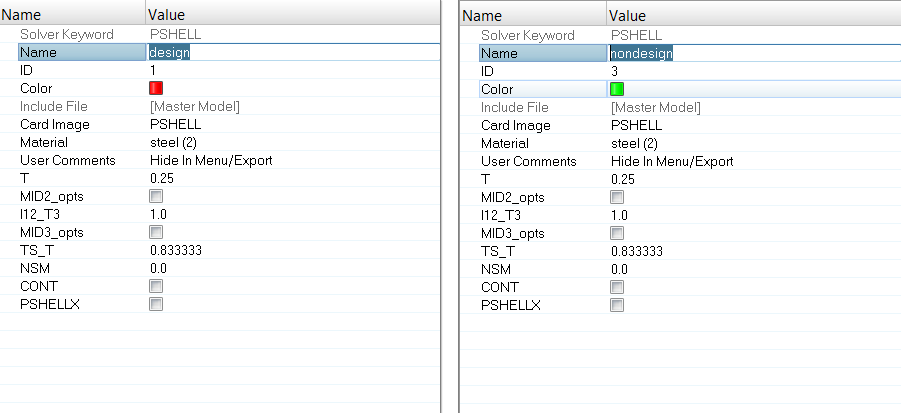
Figure 2. Updating the Thickness Value for Design and Nondesign Property Entries
Apply Loads and Boundary Conditions
The model is to be constrained using SPCs at the bolt locations. The constraints are organized into the load collector 'constraints'.
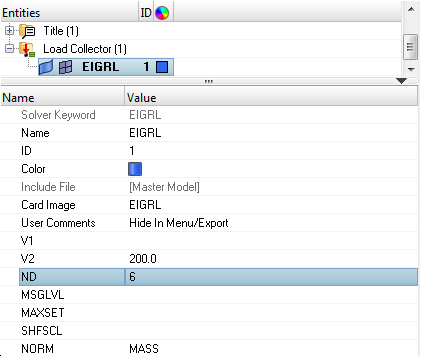
To perform a Normal Modes Analysis, a real eigenvalue extraction (EIGRL) card needs to be referenced in the subcase. The real eigenvalue extraction card is defined in HyperMesh as a load collector with an EIGRL card image. This load collector should not contain any other loads.
Create EIGRL Card
Create Constraints
Create Load Steps
An OptiStruct subcase has been created which references the constraints in the load collector constraints and the real eigenvalue extraction data in the load collector EIGRL.
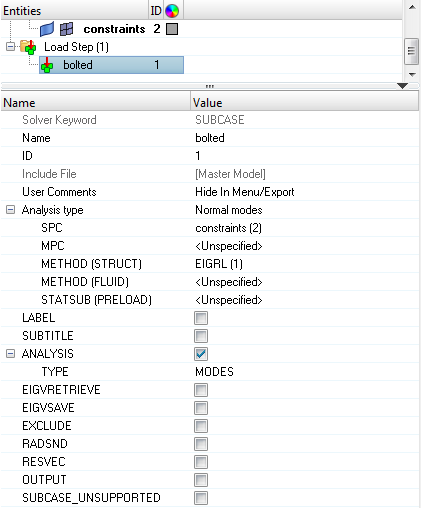
Figure 6. Creating the bolted Loadstep
Submit the Job
- sshield_complete.html
- HTML report of the analysis, providing a summary of the problem formulation and the analysis results.
- sshield_complete.out
- OptiStruct output file containing specific information on the file setup, the setup of your optimization problem, estimates for the amount of RAM and disk space required for the run, information for each of the optimization iterations, and compute time information. Review this file for warnings and errors.
- sshield_complete.h3d
- HyperView binary results file.
- sshield_complete.res
- HyperMesh binary results file.
- sshield_complete.stat
- Summary, providing CPU information for each step during analysis process.
View the Results
Eigenvector results are output by default, from OptiStruct for a Normal Modes Analysis. This section describes how to view the results in HyperView.
Load the Model and Result Files
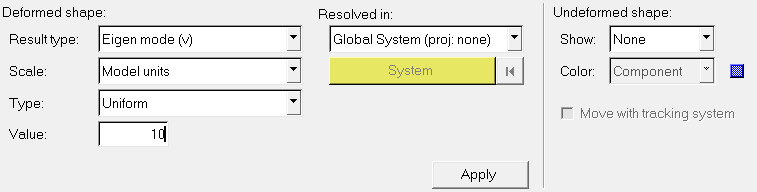
View the Deformed Shape
Summary
In this analysis, it was assumed that the bolts were significantly stiffer than the shield. If the bolts needed to be made of aluminum and the shield was still made of steel, would the model need to be modified, and the analysis run again?
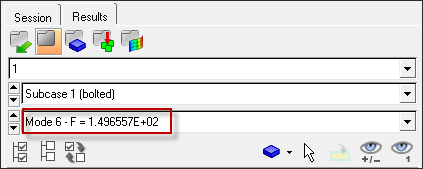
It is necessary to push the natural frequencies of the splash shield above 50 Hz. With the current model, there should be one mode that violates this constraint: Mode 1. Design specifications allow the inner disjointed circular rib to be modified such that no significant mass is added to the part. Is there a configuration for this rib within the above stated constraints that will push the first mode above 50 Hz? See tutorial OS-T: 2020 Increase Natural Frequencies of an Automotive Splash Shield with Ribs to optimize rib locations for this part.
 .
. 

 and select
and select  .
. .
.
 in the Animation toolbar.
in the Animation toolbar.