テスト番号VNL06モーメントによる荷重がかかる片持ち梁の弾性コアと最大変位を求めます。
定義
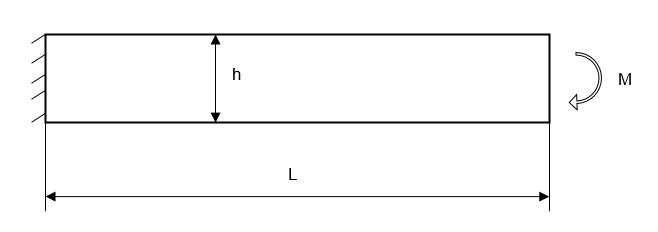
図 1.
梁の寸法はb x h x Lです。
各値の意味は次のとおりです:
- 寸法
- 値
- b
- =10 mm
- h
- =40 mm
- L
- =200 mm
梁の材料は、ひずみ応力曲線を持つ硬質プラスチックです(
図 2)。
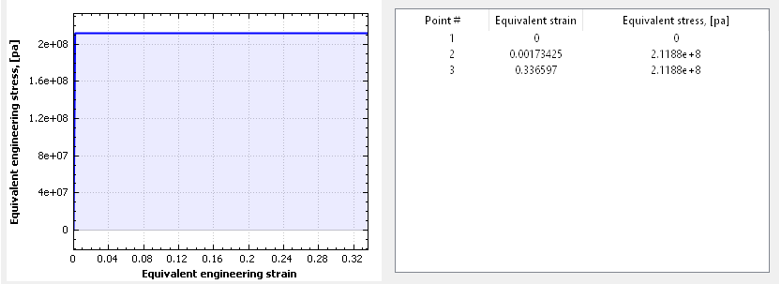
図 2.
材料特性は以下の通りです:
- 特性
- 値
- 降伏応力
-
= 2.1188e+8 Pa
- 降伏ひずみ
-
= 1.73425e-3
- ポアソン比
- 0
このスタディは、モーメント
値776.893 N*m および 847.518 N*m
基準解
プラスチック梁の曲げ理論では、梁材料には、梁の外層にあるプラスチック領域と梁の中心線にある弾性コアの2つの領域が存在すると仮定しています。
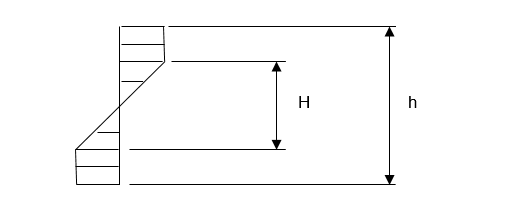
図 3. 硬化のない材料に対応する応力分布
適用されるモーメント
と梁内の弾性コアのサイズ
の関係。
(1)
ここで、
は梁の厚さです。
最大たわみ:
(2)
結果
プラスチック梁の曲げの理論は、平坦な断面は変形時にも平坦なままであるという仮説に基づいています。この基本的な前提をできるだけ忠実に再現するために、問題を2つのソリッドのアセンブリとしてモデル化しました。1つのソリッドは、曲線で定義された材料特性を持つ梁そのものを表しています(
図 2)。もう1つの小さいソリッドは、梁の端に取り付けられ、絶対的な剛体として設定されました(
図 4)。この剛体ソリッドは、モーメント
による荷重がかけられ、モーメント伝達要素として機能します。

図 4.
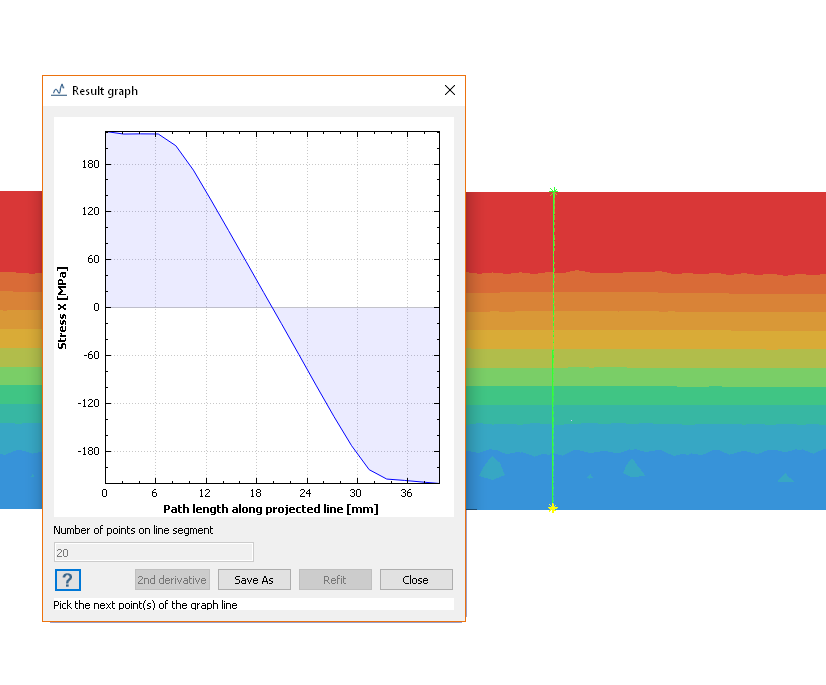
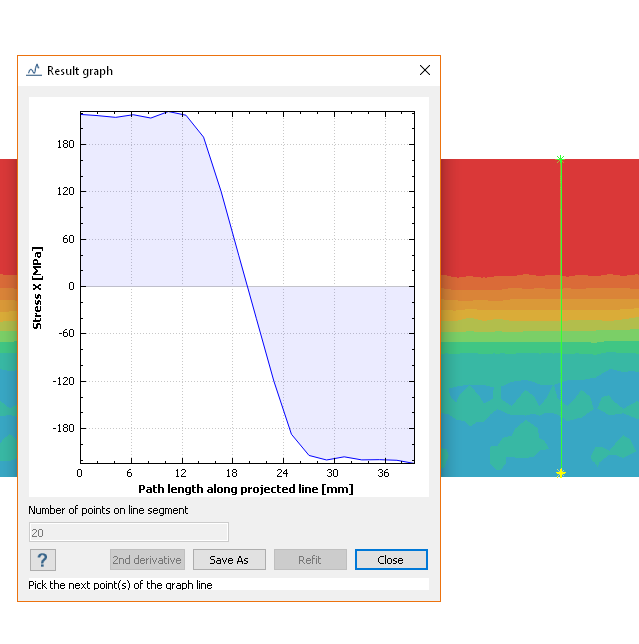
以下の表は、下の図に示されているシミュレーション結果をまとめたものです。
| モーメントM [N*m] |
SOL基準、弾性コアのサイズ [mm] |
SimSolid、弾性コアのおおよそのサイズ [mm] |
%差異 |
| 776.893 |
10.0 |
12.0 |
20.00% |
| 847.518 |
5.0 |
6.0 |
20.00% |
| モーメントM [N*m] |
SOL基準、最大変位 [mm] |
SimSolid、最大変位 [mm] |
%差異 |
| 776.893 |
3.468 |
3.351 |
-3.37% |
| 847.518 |
6.937 |
6.918 |
-0.27% |