SS-V：5080 剛体パンチ塑性
テスト番号VNL09完全塑性材料と等方的硬化材料に対する大きなブロックに押し付けられたパンチの反力を求めます。
定義
有限寸法の大きなブロックに、2D平面ひずみパンチを押し付けます。パンチは剛体と仮定し、パンチとブロック間の接触条件は摩擦のない滑りと仮定します（ラインBC）。パンチには垂直方向の下方変位Dが適用されます（図 1）。ラインABLに沿って対称条件を仮定し、ラインLKに沿って滑り条件を適用します。
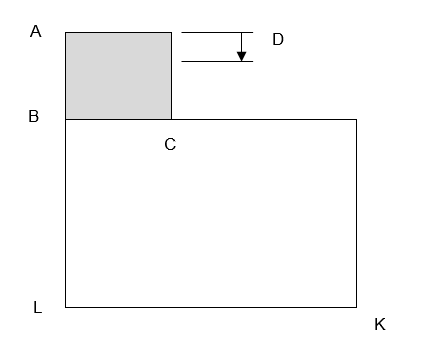
図 1.
寸法：AB = 40 mm、BC = 80 mm、BL = 160 mm、LK = 200 mm
材料特性は以下の通りです：
- 特性
- 値
- 弾性係数
- 1.e+3 MPa
- ポアソン比
- 0.3
次の2つの塑性モデルを使用します：
- 降伏応力1 MPaの弾完全塑性
- 接線係数0.1e+3 MPaの等方的硬化
結果
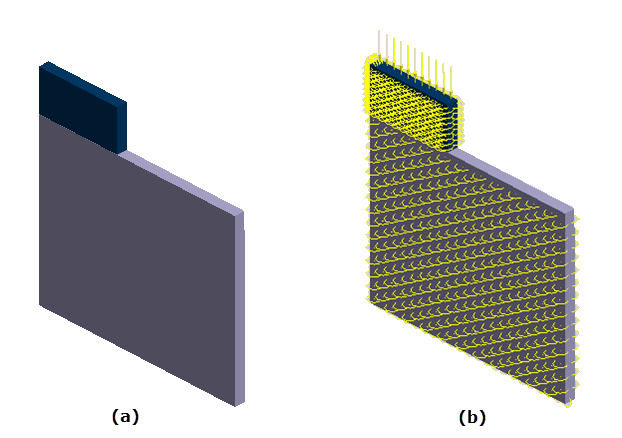
剛体パンチとベースのジオメトリは、厚さ10 mmの2つの3Dソリッドプレートを使用してシミュレートされました（図 2）。平面ひずみ条件は、プレートの側面に垂直な方向のひずみをゼロと仮定します。この条件を満たすために、プレートの両側にゼロの垂直変位を適用しました（図 2b）。
図 2.
パンチの所定の変位が6ステップで適用されました。次の表は、板厚1 mmあたりのパンチでの反力の値を示しています。
| SimSolid反力、N | 基準反力、N | |||
|---|---|---|---|---|
| D、mm | 完全塑性 | 硬化 | 完全塑性 | 硬化 |
| 0.04 | 29.57 | 29.57 | 30 | 30 |
| 0.12 | 86.95 | 87.27 | 86 | 87 |
| 0.14 | 99.93 | 100.65 | 99 | 100 |
| 0.16 | 108.22 | 111.17 | 109 | 113 |
| 0.18 | 108.87 | 113.03 | 110 | 114 |
| 0.24 | 111.75 | 122.20 | 111 | 125 |
以下の図は、パンチ変位の増分に伴う等価応力の変化を示しています。
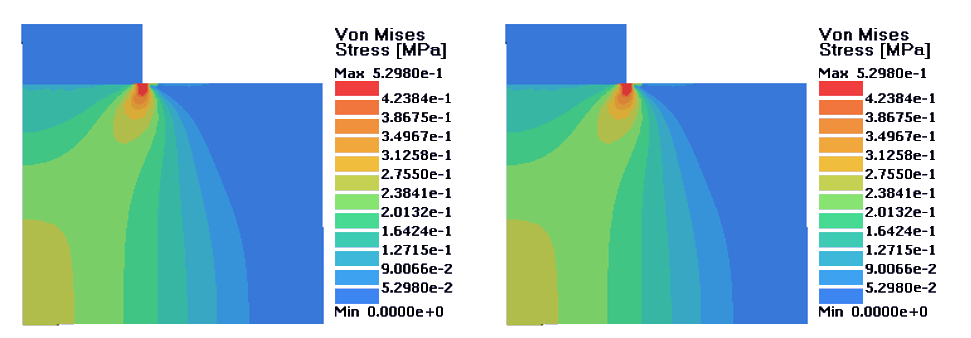
図 3. 左：完全塑性材料；右；等方的硬化材料. D = 0.04 mm
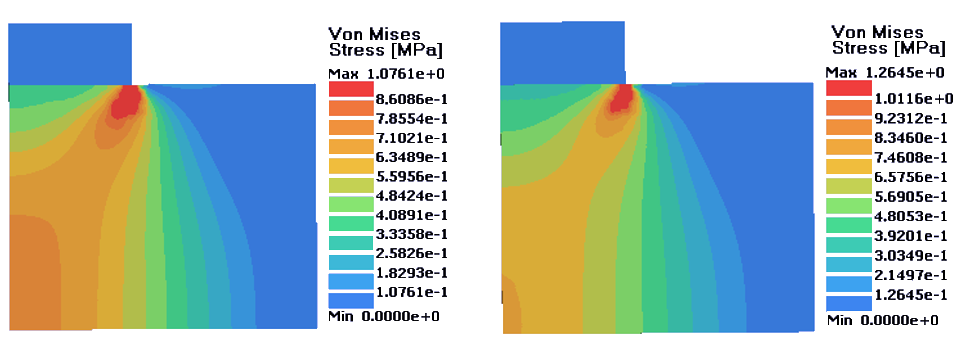
図 4. 左：完全塑性材料；右；等方的硬化材料. D = 0.12 mm
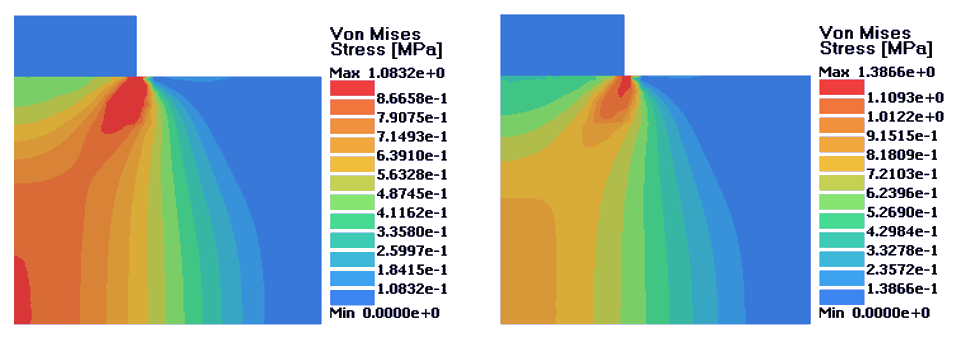
図 5. 左：完全塑性材料；右；等方的硬化材料. D = 0.14 mm
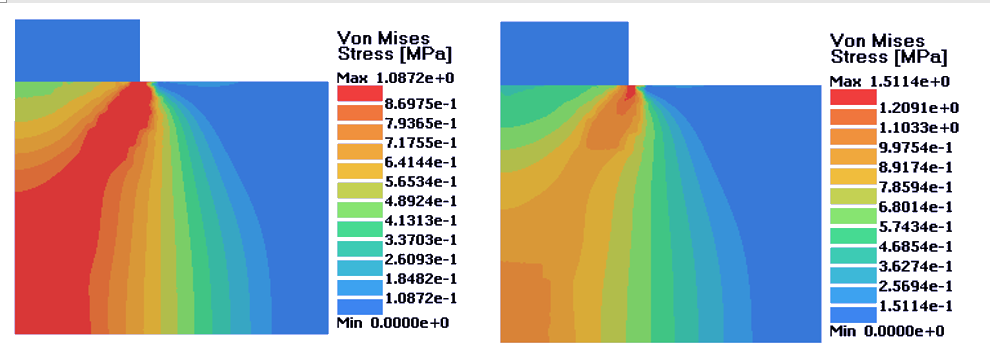
図 6. 左：完全塑性材料；右；等方的硬化材料. D = 0.16 mm
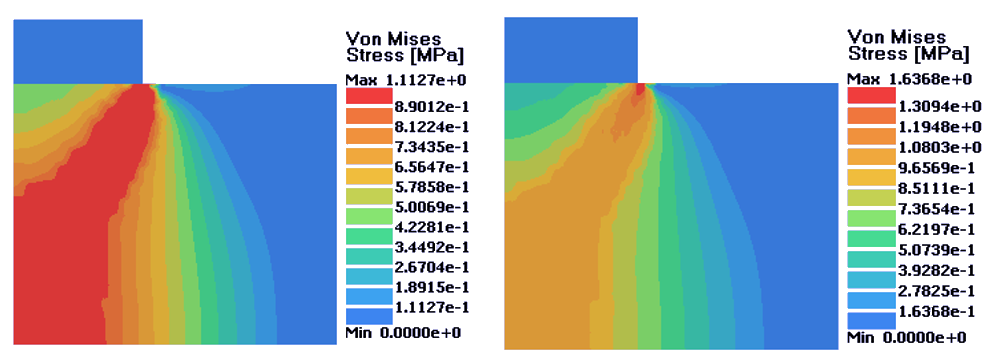
図 7. 左：完全塑性材料；右；等方的硬化材料. D = 0.18 mm
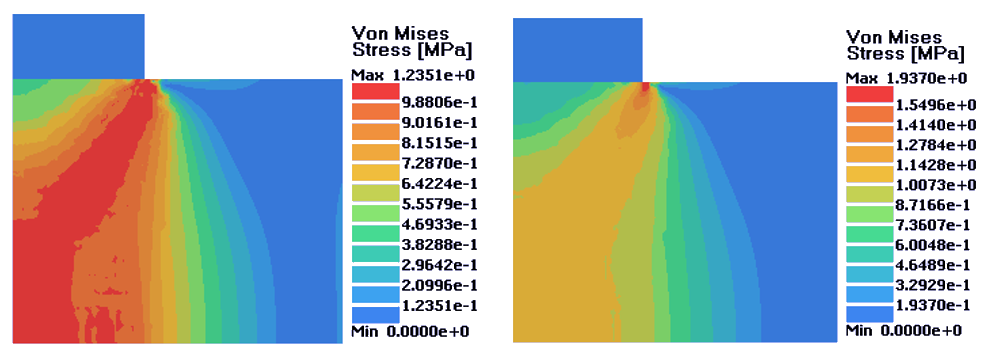
図 8. 左：完全塑性材料；右；等方的硬化材料. D = 0.24 mm
1
Test PL-7 from NAFEMS Publication R0049, “Background to Material Non-Linear Benchmarks”.