MV-7013：Composeのサブルーチンを用いたMotionSolveによる倒立振子制御

本チュートリアルでは、MotionView、MotionSolve、およびComposeを使って倒立振子を安定化させる制御システムを設計する方法について学習します。

目標は、極配置法を使ったレギュレータを設計することです。倒立振子のMDLモデルファイルは用意されています。

チュートリアルには下記の手順が含まれます：
  • 開ループシステムの安定性をチェック
  • MotionSolve線形解析を使って、線形化されたシステムのマトリクスA、B、CおよびDをエクスポート
  • Composeを使ってコントローラーを設計
  • MotionViewでコントローラをインプリメント
  • MotionSolve線形解析を使って、閉ループシステムの安定性をチェック
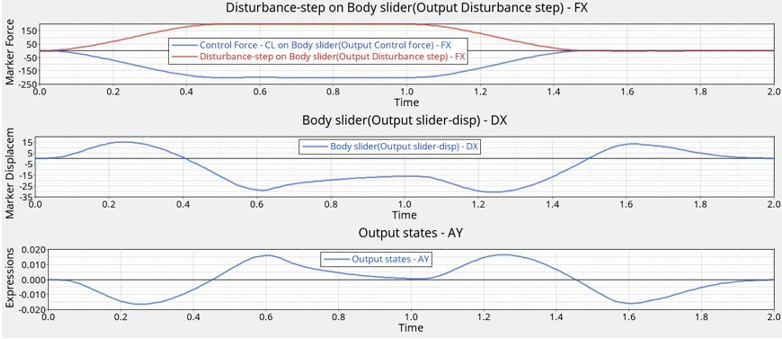
  • モデルに外乱力を追加し、MotionSolveでシミュレーションを実行

下の図はスライダー上の典型的な倒立振子です。システムは、自由度2を有し、4つの状態変数が存在します。垂直に立った振子の位置は不安定です。目標は、このコンフィギュレーションを安定させるレギュレータを設計することです。



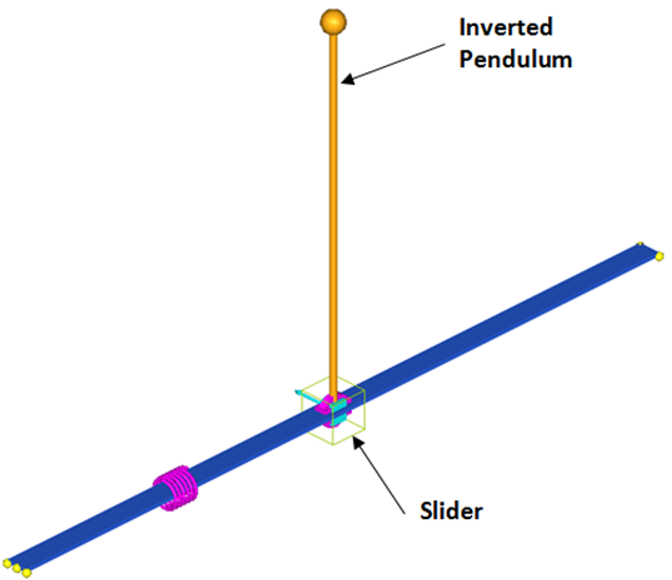
図 1. 倒立振り子モデル

目標を達成するために、完全な状態のフィードバック制御法則を見つけます。制御の入力は、全体X軸に沿ってスライダーにかかる力です。プラントの出力は、振子の全体Y軸周りの回転角度です。

最初に、[installation_directory]\tutorials\hwdesktop\mv_hv_hg\mbd_modeling\motionsolveにあるinv_pendu.mdlを、MotionViewに読み込み、作業ディレクトリに保存します。モデルのトポロジーを見てみると、本演習に必要なものはすべて、モデルに含まれていることが分かります。ただし、実行するタスクによっては、特定のエンティティをアクティブまたは非アクティブにする必要があります。

参考資料：Feedback Control of Dynamic Systems, G. G. Franklin, J. D. Powell, and A. Emami-Naeini, Third Edition, Addison Wesley.

開ループモデルの安定性のチェック

固有値を計算し、倒立振子の釣り合い状態の安定性を確認します。

  1. Projectブラウザから、Forcesをクリックします。Control Force - OLが有効になり、Control Force - CLとDisturbance-stepが無効になっていることを確認します。
  2. General Actionsツールバーで、Run をクリックします。
  3. Simulation typeドロップダウンメニューから、Static+Linearを選択します。
  4. 出力ファイル名をinv_pendu_ol_eig.xmlと指定します。
  5. MDL animation file（.maf）オプションを選択します。
  6. Runをクリックします。
  7. ランが完了したら、ソルバー実行ウィンドウとメッセージログを閉じます。
    MotionSolveにより計算された固有値は以下の一覧のとおりで、これはテキストエディタを使ってinv_pendu_ol_eig.eigファイルで確認することができます。
    NUMBER NATURAL_FREQ(HZ) DAMPING_RATIO REAL(HZ) IMAG_FREQ(HZ)
    1 1.624738E-02 1.000000E+00 -1.624738E-02 0.000000E+00
    2 4.003669E-01 1.000000E+00 -4.003669E-01 0.000000E+00
    3 0.000000E+00 1.000000E+00 5.582830E-01 0.000000E+00
    4 1.733217E+00 1.000000E+00 -1.733217E+00 0.000000E+00

    正の実数部を有する固有値が１つ存在し、現在のコンフィギュレーションではこのシステムは不安定であることを示しています。

  8. Animateをクリックします。
    結果のアニメーションH3Dファイルが隣のウィンドウに読み込まれます。
  9. Resultsブラウザから個々のモードを選択します。


    図 2.
  10. Start/Pause Animation をクリックして、モード形状を表示します。

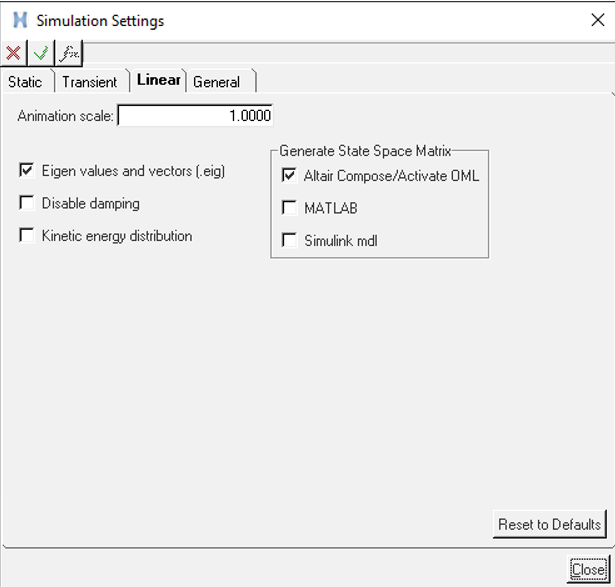
線形化されたモデルの取得

一般的に、制御システムの設計における最初のステップは、状態空間形式のシステムの線形モデルを得ることです。

ẋ = Ax+Bu

y = Cx+Du

ここで、A、B、CおよびDは状態マトリクス、xは状態ベクトル、uは入力ベクトル、yは出力ベクトルです。A、B、C、Dの各マトリクスは、（ソルバーが）選択した状態、入力、出力に依存します。ここでは、入力と出力のみを定義する必要があります。

  1. MotionViewウィンドウに戻ります。
  2. Projectブラウザから、Solver Variablesフォルダーを展開し、エンティティを確認します。
    • Control Force Variable - OLは、Control Force - OLという名の力である制御プラント入力を定義するために使用されます。この力は、スライダーのボディにかかります。この変数は、ゼロに設定されています。これは、線形化されたシステムマトリックスを正しく生成するため、MotionSolveによって必要とされます。
    • ソルバー変数Pendulum Rotation Angleは制御プラント出力を定義し、全体Y軸周りの振子の回転を計測します。
  3. Projectブラウザから、Solver Arrayフォルダーを展開し、定義されているソルバー配列を確認します。
    1. Plant-Iを選択します。この配列は、タイプPlant-Inputのソルバー配列エンティティを定義します。
    2. Solver VariableがControl Force Variable - OLにセットされていることを確認します。
    3. Use in linearizationチェックボックスが選択されていることを確認します。
    4. Plant-Oを選択します。この配列は、タイプPlant-Outputのソルバー配列エンティティを定義します。
    5. Solver VariableがPendulum Rotation Angleにセットされていることを確認します。
    6. Use in linearizationチェックボックスが選択されていることを確認します。
  4. Run をクリックします。
  5. Simulation typeドロップダウンメニューから、Linearを選択します。
  6. 出力ファイル名をinv_pendu_state_matrices.xmlと指定します。


    図 3. Composeマトリクスファイル出力を指定するSimulation SettingsダイアログのLinearタブ
  7. Simulation Settings dialog > Linear tab > General State-Space Matrixから、Altair Compose/Activate OMLを選択します。
  8. MainタブでRunをクリックします。
    inv_pendu_state_matrices.omlという出力ファイル名に対応したファイルが作成されます。
    MotionSolveソルバーによって選択された状態に関する情報は：
    • 全体Y軸周りの角変位
    • 全体X軸に沿った並進変位
    • 全体Y軸周りの角速度
    • 質量マーカーの振子ボディ中央の全体X軸に沿った並進速度
    注: Output OptionsでWrite debug infoが選択されている場合、MotionSolveは、選択された状態量をログファイルに書き込みます。


    図 4. デバッグ情報の書き込みを指定するための出力オプションダイアログのGeneralタブ。

Composeでの制御システムの設計

制御システムの設計に関する詳しい解説は、本チュートリアルでは割愛します。しかし、倒立振子を安定させるための極配置（参考資料[1] 参照）を使ったレギュレータ設計手順について、短く説明します。詳細は、制御の標準テキストおよびComposeドキュメンテーションをご参照ください。

Composeを使用して、システムが可制御（参考資料[1, 2]参照）であるかを検証します。
  1. 完全状態フィードバック制御則 u = − k ∗ xを使用します。ここで、uは制御入力、kはゲインベクトル、xは状態ベクトルです。
  2. ここで、必要な極配置がベクトルPに保管されることを前提とすると、極配置法を使ってkを計算することができます。
  3. inv_pendu_state_matrices.omlというスクリプトを読み込み、実行して、状態空間行列をCompose作業領域に読み込みます。
  4. 極Pを3Hzに配置する場合、 コマンドウィンドウに次のように入力します：
    p = 2*pi*3 * [ -1 -1 -1 -1 ] ; k = acker( A , B , p )
  5. Compose acker関数は、次のような処理や結果をもたらします：
    k = [Matrix] 1 x 4
-15020.22034 -12.86975 -2806.23453 -2.74083

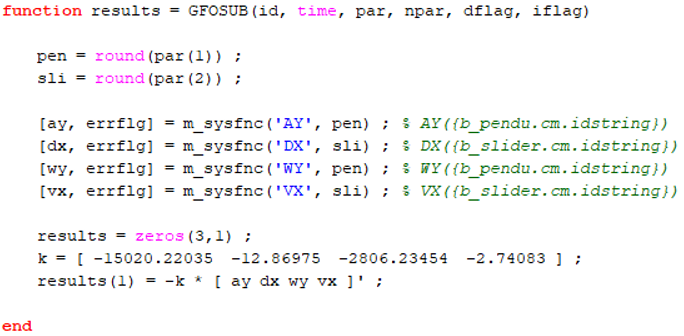
MotionViewでの制御力のインプリメント

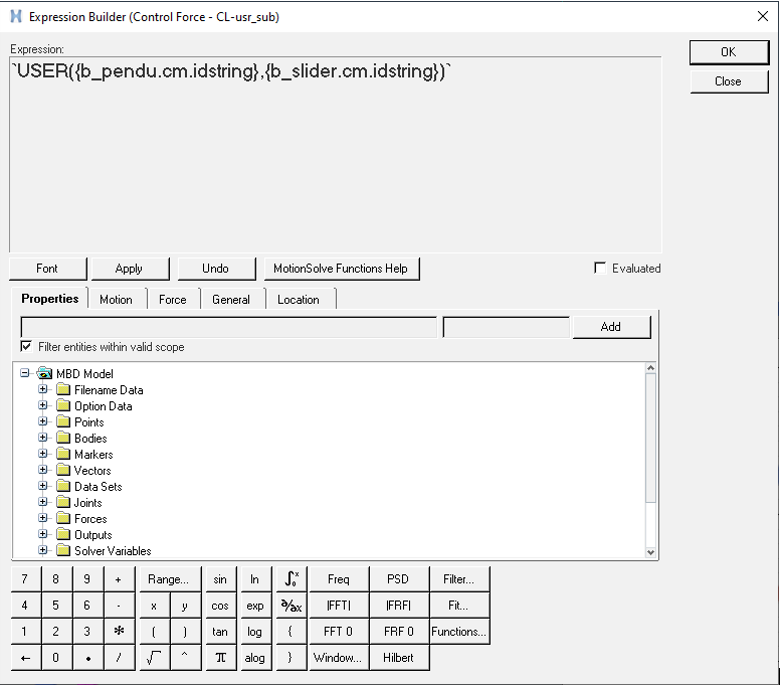
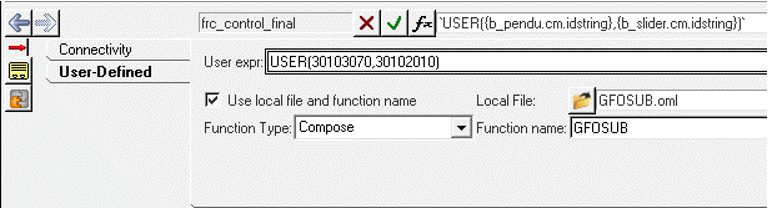
制御力は、u = − k ∗ xです。モデルには、Control Force Variable - CLという名のソルバー変数が含まれます。GFOSUBを使用してユーザー定義のComposeスクリプトでフォースエンティティを置き換えます。GFOSUBは、m_sysfncを介してシステムの状態にアクセスします。

Composeスクリプトの記述

  1. Composeで新しいOMLシステムを作成します。
  2. 次のように入力して、関数GFOSUBを定義します。
    function results = GFOSUB(id, time, par, npar, dflag, iflag)
    このサブルーチンの詳細については、GFOSUBを参照してください。
    parには、振子とスライダーのCMマーカーのIDが含まれます。IDの定義は、後述するMotionViewで行います。ロバスト性のために、IDが整数であることを確認します。
  3. 新しい行で、以下を入力します：
    pen = round(par(1)) ; sli = round(par(2)) ;
  4. m_sysfncを使用して、変数として保存します。次の値を入力します： 
    [ay, errflg] = m_sysfnc('AY', pen);
[dx, errflg] = m_sysfnc('DX', sli);
[wy, errflg] = m_sysfnc('WY', pen); 
[vx, errflg] = m_sysfnc('VX', sli);
  5. 倒立振子の制御力を入力します。これは、ゲインベクトル(k)および状態ベクトル(x)の要素間のドット積です。GFOSUBをボディ（Force_Vector_OneBody）に与えるため、返される配列は3次元である必要があります。 
    results = zeros(3,1) ;
k = [ -15020.22035 -12.86975 -2806.23454 -2.74083 ] ;
results(1) = -k * [ ay dx wy vx ]' ;
  6. endコマンドで関数を閉じます。
    以下に完成した関数の例を示します：


    図 5.
  7. このファイルをGFOSUB.omlとして<作業ディレクトリ>に保存します。

Composeスクリプトの実装

  1. Projectブラウザから、Forcesをクリックします。Control Force – OLを無効にし、Control Force – CLを有効にします。
  2. ConnectivityタブからUser-defined propertiesを選択します。
  3. User-DefinedタブでForceの値をExpression Builderで編集し、振子とスライダーのマーカーidstringを含めます。


    図 6.
  4. OKをクリックします。
  5. Use local file and function nameを選択し、Function TypeドロップダウンメニューからComposeを選択します。
  6. を使って、自身の<作業ディレクトリ>からGFOSUB.omlを選択します。
  7. Function nameがGFOSUBに設定されていることを確認します。


    図 7.

閉ループシステムの安定性のチェック

  1. Run panel > Simulation typeドロップダウンメニューからLinearを選択します。
  2. 出力ファイル名をinv_pendu_cl_eig.xmlと指定し、Run をクリックします。
    固有値は下に示すとおり与えられます。
    NUMBER NATURAL_FREQ(HZ) DAMPING_RATIO REAL(HZ) IMAG_FREQ(HZ)
    1 2.681249E+00 1.000000E+00 -2.681249E+00 0.000000E+00
    2 3.380362E+00 1.000000E+00 -3.380362E+00 0.000000E+00
    3 2.989457E+00 9.933140E-01 -2.969470E+00 3.451144E-01
    4 2.989457E+00 9.933140E-01 -2.969470E+00 -3.451144E-01

    これらはすべて実数部が負で、システムは安定していることが分かります。負の実数部は、必要な極（3Hz）に近い点にご注目ください。

外乱力の追加と過渡シミュレーションの実行

  1. Projectブラウザから、Forcesをクリックし、Disturbance-stepを有効にします。
    この力は、過渡解析の際に振子に小さな乱れを生じさせます。制御装置の目的は、倒立振子が倒れないように外乱を補正することです。外乱はステップ関数を使用して定義されます：
    1. Fx=`step(TIME,.1,0,.5,50) + step(TIME,1,0,1.5,-50)`
    2. Fy=0
    3. Fz=0
  2. Projectブラウザから、Outputsをクリックし、 Output control force - finalとOutput Disturbance stepを有効にします。
  3. ツールバーから、Run をクリックします。
  4. Simulation typeドロップダウンメニューから、Transientを選択します。
  5. 出力ファイル名をinv_pendu_dyn.xmlと指定します。
  6. End timeとPrint intervalをそれぞれ3.0と0.01に設定します。
  7. MainタブでRunをクリックします。
  8. ジョブが終了したらソルバーウィンドウを閉じ、inv_pendu_dyn.mrfを使って新しいHyperGraphページに以下の結果をプロットします。
    Output Y-Type Y-Request Y-Component
    制御力 Marker Force REQ/70000014 Control Force - CL on Body slider(Output control force - final) FX
    外乱力 Marker Force REQ/70000017 Disturbance-step on Body slider(Output Disturbance step) FX
    スライダー変位 -X Marker Displacement REQ/70000006 Body slider(Output slider-disp) DX
    振子の角変位 Expressions REQ/70000016 Output Pendu rotation F2
  9. 外乱力、制御力、スライダーのx変位、振子の角変位のプロットを下に示します。


    図 8. 外乱力と制御力、およびスライダーの並進変位と振子の角変位のプロット