粒子は6方最密充填、面心立方また立方ネットのパッキングで作成される必要があります。
6方最密充填および面心立方は、Radioss での使用に推奨され、同様の結果を与えます。面心立方の粒子分布は、HyperMesh SPHパネルを使って作成できます。6方最密充填ネットを作成するためのHyperMesh Tcl マクロは、Altair Connectウェブサイトから入手が可能です。
6方最密充填ネット
ある面心立方ネットは6方最密充填分布を表し、これはネットを構築するのに有用です。
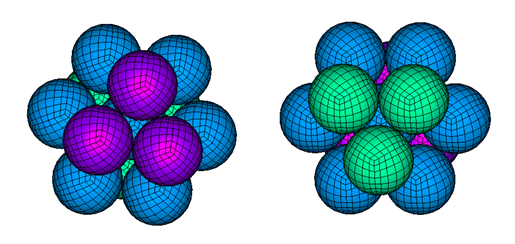
図 1. 6方最密充填ネットの局所ビュー
図 2. 面心立方ネットの透視ビュー
6方最密充填ネットの分布は、Hexagonal Compact Net Tcl スクリプト用にAltair Connectで検索すると入手できるTcl スクリプトを使ってHyperMesh で作成することができます。このスクリプトを使用する際は、任意の粒子とその近傍の最も近い粒子との間のピッチまたは距離がh 0
粒子m p /PROP/SPH で定義されます。
SPH粒子質量は、材料密度
ρ
と6方最密充填ネットのピッチ
h 0 に関連します。この粒子質量は、次のように計算することができます:
(1)
m
p
≈
h
0
3
2
ρ
空間はそれぞれの粒子を取り巻く多面体に分割できるため、それぞれの体積は:
(2)
V
p
=
h
0
3
2
体積内の離散化の差により、質量は以下によってより正確になり得ます:
(3)
m
P
=
ρ V
n
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGTbWaaSbaaSqaaiaadcfaaeqaaOGaeyypa0ZaaSaaaeaacqaH
bpGCcaWGwbaabaGaamOBaaaaaaa@3F79@
ここで、
V
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGwbaaaa@39B3@
粒子によって満たされる全体積
n
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGUbaaaa@39CB@
体積内に分布される粒子の全数
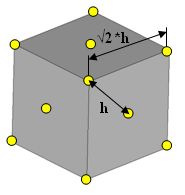
6方最密充填ネットの場合、/PROP/SPH 内の推奨されるスムージング長h は、粒子間の最短距離であるピッチh 0 h 0
以下の一覧は、
/PROP/SPH で異なるスムージング長
h が使用されている際に、近傍の粒子の数を示します。シミュレーションの精度と計算コストは、スムージング長が大きくなるにつれて向上します。
表 1. 6方最密充填ネット内の隣接粒子の数
距離 d
距離dの粒子の数
距離d内の粒子の数
h 0 12
12
2
h
0
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aadaGcaaqaaiaaikdaaSqabaGccaWGObWaaSbaaSqaaiaaicdaaeqa
aaaa@3B8C@
6
18
3
h
0
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aadaGcaaqaaiaaiodaaSqabaGccaWGObWaaSbaaSqaaiaaicdaaeqa
aaaa@3B8D@
24
42
2h 0
12
54
5
h
0
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aadaGcaaqaaiaaiwdaaSqabaGccaWGObWaaSbaaSqaaiaaicdaaeqa
aaaa@3B8F@
24
78
面心立方
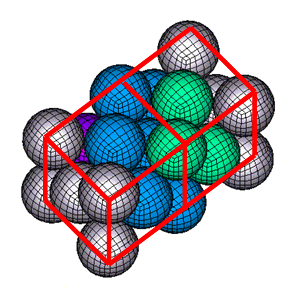
面心立方は、14のグループ内の粒子をアレンジし、コーナーと立方体の各面の中央を生成します。
図 3.
6方最密充填ネットと同様、各粒子は12個の隣接粒子を有し、粒子の質量は:
(4)
m
P
=
ρ V
n
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGTbWaaSbaaSqaaiaadcfaaeqaaOGaeyypa0ZaaSaaaeaacqaH
bpGCcaWGwbaabaGaamOBaaaaaaa@3F79@
面心立方の場合、/PROP/SPH で推奨されるスムージング長h は、sphメッシュがHyperMesh で作成された際に入力されたピッチです。ピッチh 0 h 0 h 0
シンプルな立方ネット
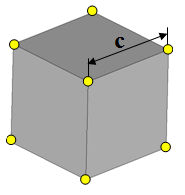
c をネット内のそれぞれの基本的な立方の側部の長さとします。
図 4.
粒子の質量
m p は、材料の密度
ρ
とネットのサイズ
c に、次の式を用いて関連付けられるべきです:
(5)
m
p
=
c
3
ρ
表 2. 立方ネットの隣接粒子の数
距離d
距離dの粒子の数
距離d内の粒子の数
c
6
6
2
c
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aadaGcaaqaaiaaikdaaSqabaGccaWGJbaaaa@3AA1@
12
18
3
c
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aadaGcaaqaaiaaikdaaSqabaGccaWGJbaaaa@3AA1@
8
26
2c
6
32
5
c
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aadaGcaaqaaiaaikdaaSqabaGccaWGJbaaaa@3AA1@
24
56
6
c
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aadaGcaaqaaiaaikdaaSqabaGccaWGJbaaaa@3AA1@
24
80
2
c
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aadaGcaaqaaiaaikdaaSqabaGccaWGJbaaaa@3AA1@
12
92
3c
6
98
立方ネットを用いた経験から、引張の不安定の問題を解決するには、面心立方または6方最密充填ネットよりも大きいスムージング長が必要です。スムージング長が大きいほど、計算コストは高くなります。これは、より多くの近傍粒子が、各粒子についての計算に含まれなければならないせいです。
立方ネットの場合、/PROP/SPH でスムージング長h が1.25cから1.5cまでの間にあることが推奨されます。