可研究结构中点焊的疲劳性能。
目前,仅支持基于应力-寿命 (SN) 的点焊疲劳分析。点焊位置由三个属性定义:薄片 1、薄片 2 和焊点熔核。
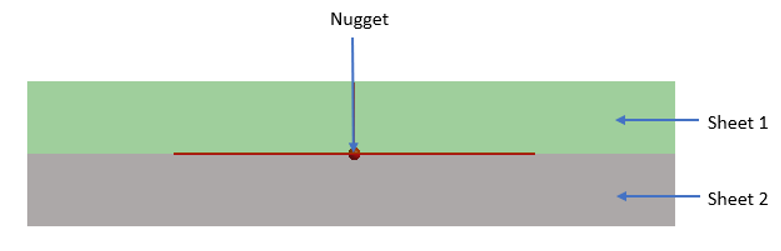
Figure 1. 点焊疲劳
执行
点焊的疲劳分析包括在三个不同的位置检查焊缝,薄片和焊点熔核,这是基于 Rupp 等人发表的一篇论文。确定焊点熔核位置处的截面力和力矩,然后计算薄片和焊点熔核的相应应力。然后再使用这些应力并结合雨流计数和 SN 方法来计算疲劳损伤。
以下各部分说明了如何计算这三个位置的应力和随后的损伤。
薄片位置(1 或 2)
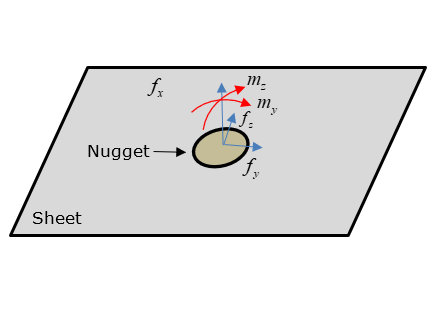
Figure 2. 薄片位置上的力和目标力矩
通过考虑焊点熔核处的力和力矩来计算薄片的径向应力。径向应力
作为载荷-时间历史中每个点的
的函数计算如下:
(1)
其中,
(2)
(3)
(4)
(5)
(6)
(7)
-
- 焊缝单元的直径
-
- 损伤计算时考虑的薄片厚度
-
,
,
- 比例因子
-
,
,
- 直径指数
-
,
,
- 厚度指数
等效于 Rupp 方法:
等效径向应力以
为间隔进行计算(默认值=18度)。可以通过改变点焊求解设中的角度数量字段来修改
的值。然后,采用雨流循环计数法计算各角度下的疲劳寿命和损伤 (
)。然后选择最严重的损伤值进行输出。对另一个薄片也采用类似的方法。
焊点熔核位置
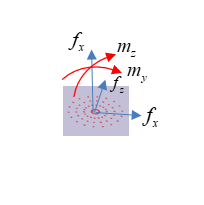
Figure 3. 焊点熔核横截面的力和力矩
绝对最大主应力是使用梁单元的剪切应力和弯曲应力作为载荷-时间历史中每个点的函数
来计算的,如下所示:
(8)
(9)
其中,
(10)
(11)
(12)
(13)
(14)
(15)
-
- 焊缝单元的直径
-
- 损伤计算时考虑的薄片厚度
从
和
计算每个
的等效最大绝对主应力。这些应力被用于后续的疲劳分析。采用雨流循环计数法计算各角度下的疲劳寿命和损伤 (
)。然后选择最严重的损伤值进行输出。


