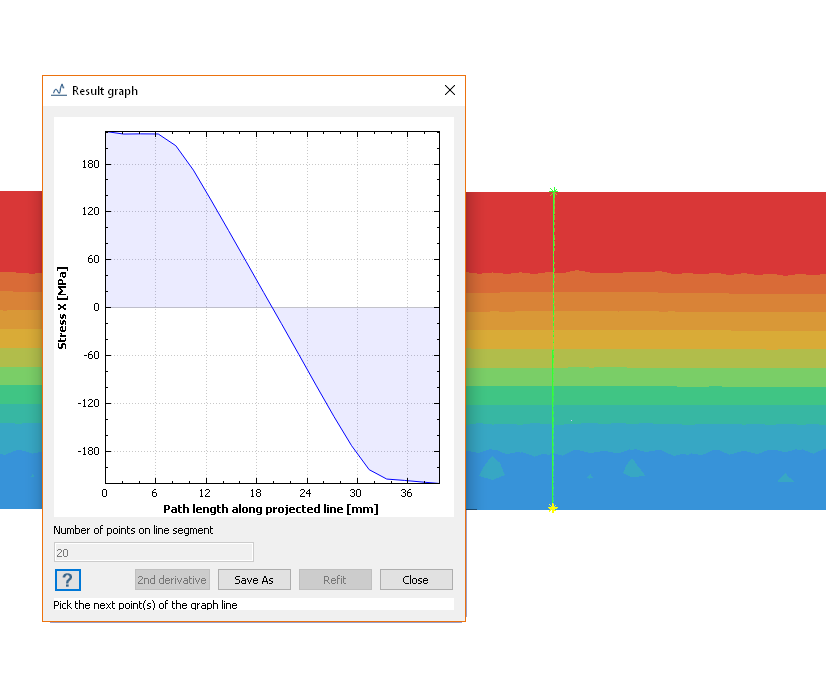
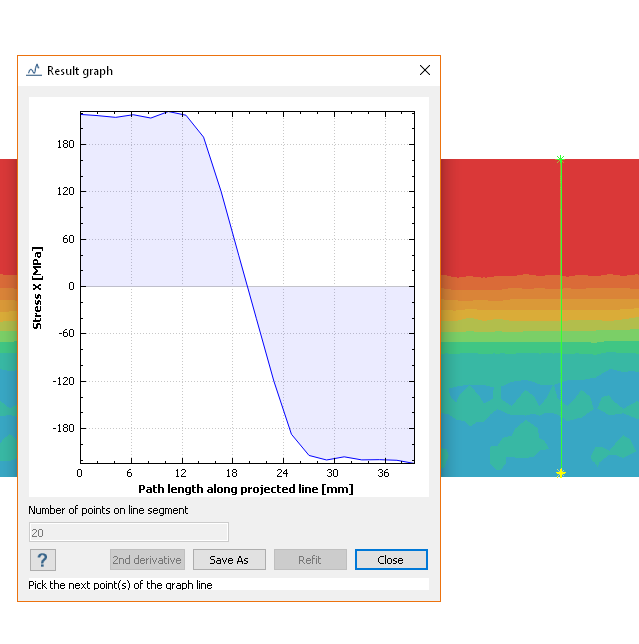
测试编号:VNL06求出受力矩作用的悬臂梁的弹性核心和最大位移。
定义
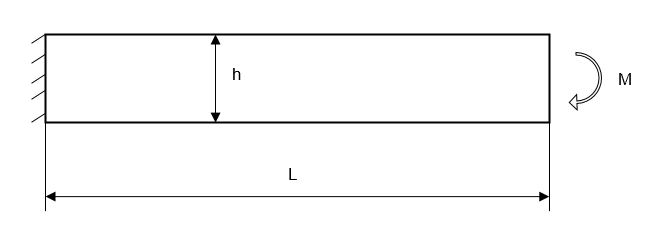
Figure 1.
梁尺寸为 b x h x L。
其中,
- 尺寸
- 值
- b
- =10 mm
- h
- =40 mm
- L
- =200 mm
梁的材料为刚性塑性,具有应变-应力曲线 (
Figure 2)。
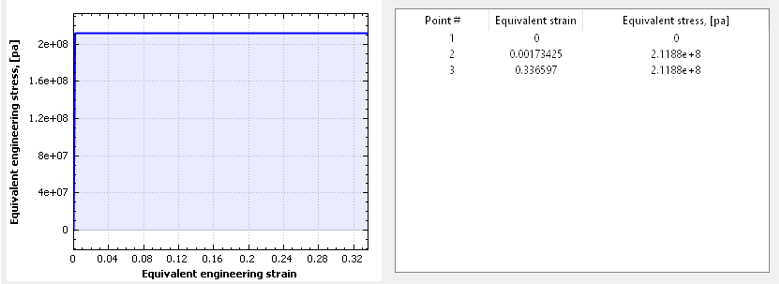
Figure 2.
材料属性为:
- 属性
- 值
- 屈服应力
-
= 2.1188e+8 Pa
- 屈服应变
-
= 1.73425e-3
- 泊松比
- 0
该研究是针对以下力矩
值进行的:776.893 N*m and 847.518 N*m
参考解
塑性梁弯曲理论假定梁材料中存在两个区域:梁外层的塑性区和梁中心线的弹性核心区。
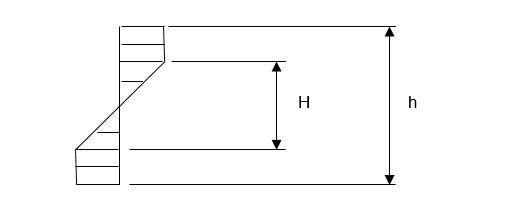
Figure 3. 未硬化材料的相应应力分布
所施加的力矩
梁中弹性核心尺寸
之间的关系。
(1)
其中,
是量厚度。
最大挠度:
(2)
结果
塑性梁的弯曲理论是基于平截面在变形过程中保持平面的假设。为了尽可能接近这一基本假设,将问题建模为两个实体的集合。一个实体表示梁本身,其材质属性由曲线定义 (
Figure 2)。另一个小实体附着在梁端,并被设置为绝对刚体 (
Figure 4)。刚性实体被施加了力矩
,作为力矩传递单元。

Figure 4.
下表总结了下图中描述的模拟结果。
| 力矩 M [N*m] |
SOL 参考,弹性核心尺寸 [mm] |
SimSolid,近似弹性核心尺寸 [mm] |
% 差异 |
| 776.893 |
10.0 |
12.0 |
20.00% |
| 847.518 |
5.0 |
6.0 |
20.00% |
| 力矩 M [N*m] |
SOL 参考,最大位移 [mm] |
SimSolid,最大位移 [mm] |
% 差异 |
| 776.893 |
3.468 |
3.351 |
-3.37% |
| 847.518 |
6.937 |
6.918 |
-0.27% |