What is a computation point?
Definition
A computation point is a point in the space of the computation domain, on which the user can evaluate a spatial quantity.
A computation point is defined by its coordinates.
Use
A computation point is used within:
- a session of quantities computation on points quantities computation on points
- the definition of a path
- the definition of a sensor of pont type (spatial quantity on a point )
Computation point: location
A computation point can be located in the study domain, from a point of view of the geometry, mesh, physics and kinematics as that is presented in the table below. Details on these various types of location are presented in the following blocks.
| From a point of view of … | … a computation point is located … |
|---|---|
| geometry |
on a geometric support (point, face, line, volume) |
| mesh |
on a mesh support (line, face, volume element) |
| physics |
in a physical region (line, face, volume region) |
| kinematics |
in a mechanical set (fixed, compressible, mobile) |
Location in relation to the geometry
From a point of view of the geometry, a computation point is:
- either any point in the space of the study domain
- or a point which is based on an existing geometrical support (a point, a line, a face)
The user can define a computation point by means of the methods presented in the table below.
| Computation point | Mode of definition | |
|---|---|---|
| graphical (mouse click) | numerical (coordinates) | |
| any | - | - |
| on a face | graphical free |
constraint by face + choice of a face support |
| on a line | graphical by line |
constraint by line + choice of a line support |
| on a point | graphical by point |
constraint by point + choice of a point support |
| → |
the cursor is automatically placed on the nearest support (face / line / point) |
the point is projected on the desired support (face/ line / point) |
From a digital point of view, the software carry out a projection of the specified entity (point, line or face) coordinates. This projection has a precision of on epsilon ( relative accuracy). The coordinates must be very close to the geometric entity.
Location in relation to the mesh
From a point of view of the mesh, a computation point belongs to a volume, face or line element.
Location in relation to the physics
From a point of view of the physics, a computation point is located in a physical region: volume region, face region or line region.
If a computation point is in interface between volume regions , the user does specify the region (and thus the formulations used) for computation.
In general, the location in the thickness or in the cross-section is not necessary to define for thin or filiform regions of material region type (with material and thickness or cross-section), because the computed spatial quantity is considered constant in the thickness.
The only exception are the following specific regions (3D Steady state AC Magnetic application):
- thin conducting region with hyperbolic variation of current density in the thickness
- region in the surface impedance formulation
For these regions the user must specify the position in the thickness*.
Location in relation to the kinematics
Within a kinematic coupling, there are many mechanical sets – fixed, mobile, compressible (possibly). The computation point is located in one of the mechanical sets.
If a computation point is in interface between mechanical sets, the user does specify the mechanical set on which the point must be captured. Indeed, various techniques of the movement processing are based on a separation of points, lines, nodes, … on the dissociation surface (see Equations / re-meshing techniques ).
If the computation point is in interface several mechanical sets, the user must first choose the visualization of one of surfaces before carrying out the capture as that is presented in the figure below.
Device :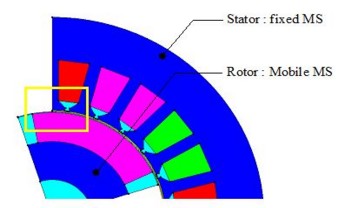
|
Selection of the point with rotor visualization |
Selection of the point with stator visualization |
|---|---|
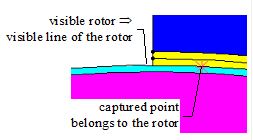
|
|
And if there is motion…
The location of a point is known as “static” when the point is defined for a computation step.
If the point should be defined for various computation steps, it is necessary to take into account the motion and to define it in relation to one of the mechanical sets. It is necessary in the case of a path and for a point sensor (spatial quantity on a point).