Soft Soil Tireモデル
AltairのSoft Soil Tireモデルは、粘土質、乾燥砂、表土、氷で覆われた雪面などの圧縮可能なサーフェス上でタイヤが示す動的な挙動をシミュレートする方法を提供します。
タイヤと土のプロパティファイル例がインストール先の<Installation>\hwdesktop\hw\mdl\autoentities\properties\Tires\ALTAIR_SOFTSOILにあります。
理論的な捉え方
現在のタイヤモデルでは、土の変形に応じて最終的に法線方向とせん断方向に応力が発生する場合、その変形は2つの独立した効果と見なされます。具体的には、垂直方向(圧力と沈下量の関係)と水平方向(せん断応力とせん断変位量との関係)で土の強度が考慮されます。
圧力と沈下量の関係
路面が均一であると仮定すると、その路面の圧力と沈下量の関係は図1に示した形態のいずれかとなり、Bekkerが提唱した次の経験式で特性記述できます。[1]
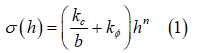
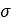 は圧力、
は圧力、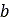 は矩形接触パッチ領域の幅、
は矩形接触パッチ領域の幅、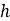 は沈下量、
は沈下量、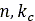 と
と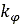 は圧力と沈下量に関連するパラメータです。さまざまな路面について、これらのパラメータの代表値が付録Aに示されています。
は圧力と沈下量に関連するパラメータです。さまざまな路面について、これらのパラメータの代表値が付録Aに示されています。
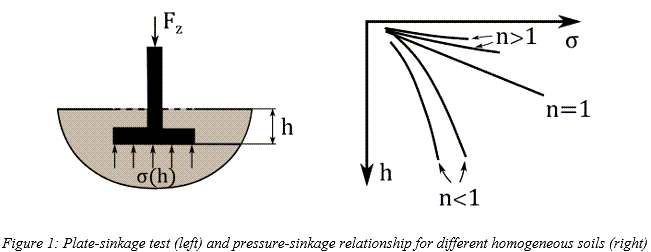
土の破壊
土の破壊に関してはさまざまな基準が提唱されています。幅広く使用されている基準の一つであるMohr-Coulomb基準では、土の最大せん断強度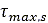 を次のように規定しています。
を次のように規定しています。
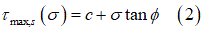
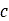 は見掛け凝集力、
は見掛け凝集力、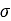 は法線方向応力、
は法線方向応力、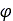 は材料の内部せん断抵抗が示す角度です。上記の各種パラメータは、図2に示すように、さまざまな圧力下でのせん断テストから導かれます。
は材料の内部せん断抵抗が示す角度です。上記の各種パラメータは、図2に示すように、さまざまな圧力下でのせん断テストから導かれます。
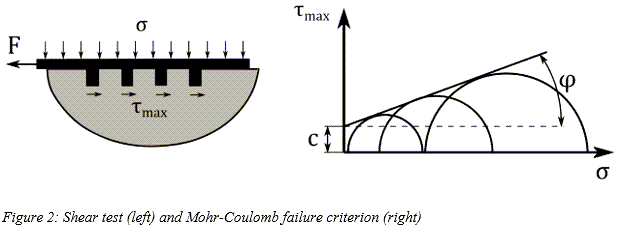
タイヤと路面との相互作用
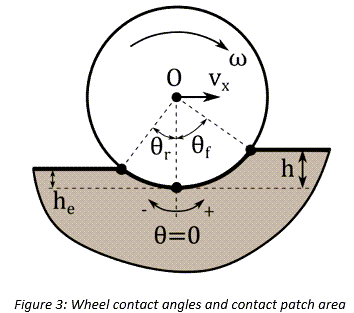
接触パッチ領域
ホイールが移動する場合は、以下の式を使用してタイヤの沈下量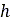 、タイヤの半径
、タイヤの半径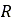 、弾性沈下量
、弾性沈下量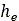 の関数として接触パッチ領域を定義できます。
の関数として接触パッチ領域を定義できます。
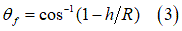
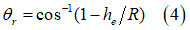
Normal Stress
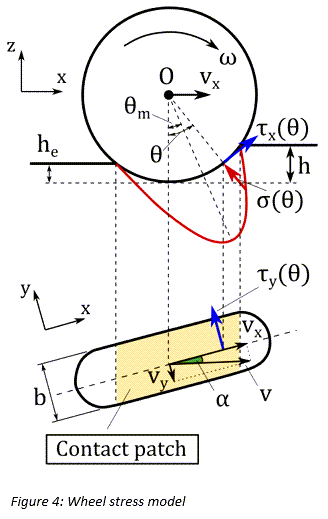
Bekkerが提唱した圧力と沈下量の関係(式(1))を使用し、ホイール角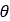 の関数としてタイヤの法線方向応力の分布を計算できます[2]。具体的には次のようになります:
の関数としてタイヤの法線方向応力の分布を計算できます[2]。具体的には次のようになります:
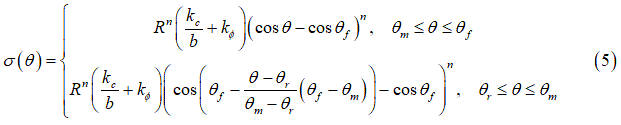
bはタイヤ幅です。また、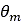 は、法線方向応力が最大になったときのホイール角で[2]、次のように求めることができます。
は、法線方向応力が最大になったときのホイール角で[2]、次のように求めることができます。
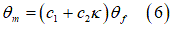
上記の式で、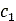 と
と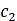 はホイールと土の相互作用に依存するパラメータ、
はホイールと土の相互作用に依存するパラメータ、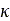 は縦方向のスリップ量、
は縦方向のスリップ量、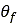 はタイヤの進入角度です。路面例ごとの
はタイヤの進入角度です。路面例ごとの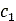 と
と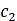 の値が付録Aにあります。
の値が付録Aにあります。
また、土による減衰の効果を考慮するために式(5)を修正できます[3]。その場合の法線方向応力の分布は次のようになります。
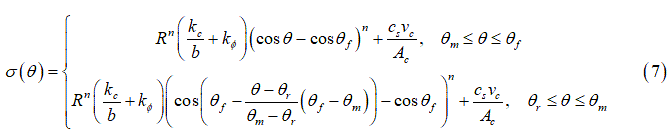
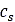 は土による減衰、
は土による減衰、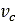 は速度あたりの土の圧縮率、
は速度あたりの土の圧縮率、 は接触パッチの面積です。
は接触パッチの面積です。
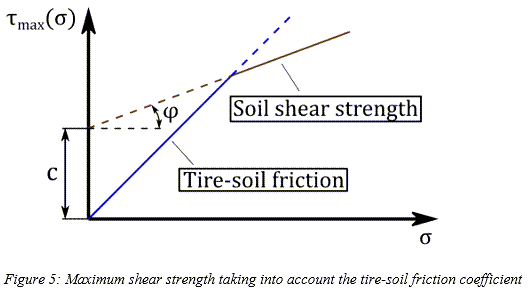
摩擦係数の影響
すでに触れたように、土の最大せん断強度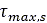 は、Mohr-Coulomb破壊基準に基づいて式(2)を使用することで計算できます。また、タイヤと土との間の最大せん断強度
は、Mohr-Coulomb破壊基準に基づいて式(2)を使用することで計算できます。また、タイヤと土との間の最大せん断強度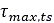 は、圧力
は、圧力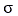 と摩擦係数
と摩擦係数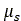 の関数として次のように近似できます。
の関数として次のように近似できます。
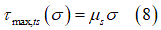
これにより、タイヤと土の摩擦を考慮するために、せん断応力の計算に最小せん断強度(土・タイヤと内部土壌)が使用されます[4]。
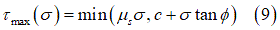
この摩擦係数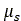 の一般的な値は0.3~1.0の範囲ですが、タイヤの材料と土中の水分によって大幅に変化します[4]。
の一般的な値は0.3~1.0の範囲ですが、タイヤの材料と土中の水分によって大幅に変化します[4]。
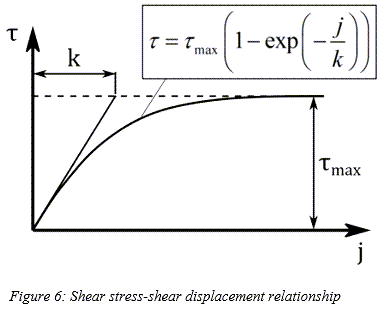
Shear Stress
せん断応力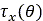 と
と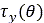 は、同じ式を使用して計算します[5]、[6]。
は、同じ式を使用して計算します[5]、[6]。
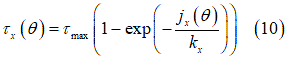
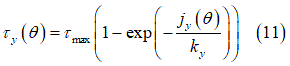
上記の式にある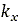 と
と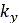 はせん断変形係数を表し、以下の式で求めることができます。
はせん断変形係数を表し、以下の式で求めることができます。
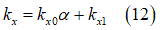
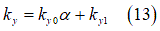
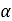 は、タイヤのスリップ角です。また、土の変形量
は、タイヤのスリップ角です。また、土の変形量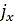 と
と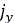 は、ホイール角
は、ホイール角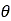 の関数として次のように定式化できます[2]、[7]。
の関数として次のように定式化できます[2]、[7]。
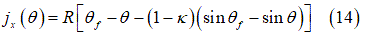
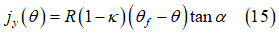
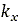 と
と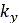 の一般的な値は、以下の刊行物で取り上げられています。
の一般的な値は、以下の刊行物で取り上げられています。- ‘Terramechanics-based Model for Steering Maneuver of Planetary Exploration Rovers on Loose Soil’ by G. Ishigami and K. Yoshida, 2007 [5]
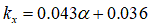 [m]
[m]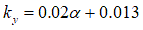 [m]
[m]
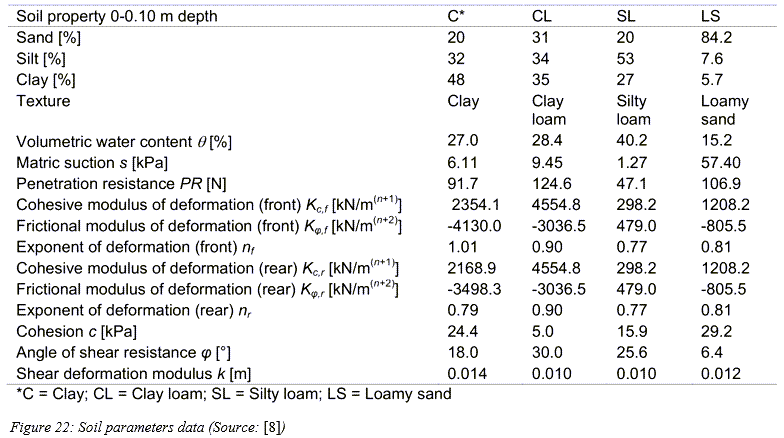
- ‘Soil-tire interaction analysis for agricultural tractors: Modeling of traction performance and soil damage’ by A. Battiato, 2014 [8]
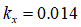 [m](粘土質の場合)
[m](粘土質の場合)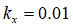 [m](粘土質ロームの場合)
[m](粘土質ロームの場合)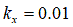 [m](シルト質ロームの場合)
[m](シルト質ロームの場合)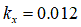 [m](ローム性砂の場合)
[m](ローム性砂の場合)
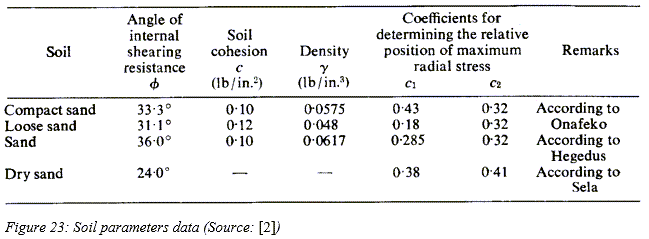
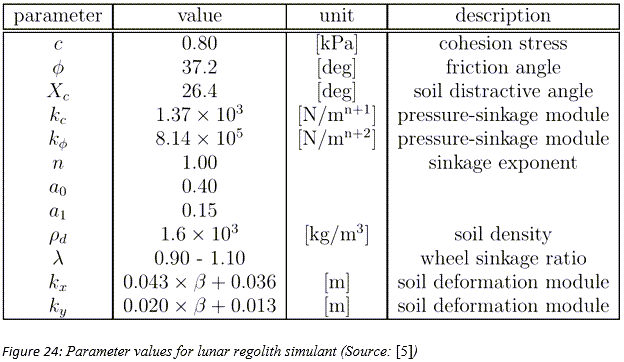
- ‘Terramechanics-based analysis for slope climbing capability of a lunar/planetary rover’ by K. Yoshida and G. Ishigami, 2004 [9]
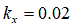 [m](乾燥砂の場合)
[m](乾燥砂の場合)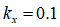 [m](レゴリス類似石の場合)
[m](レゴリス類似石の場合)
- ‘Analysis of off-road tire-soil interaction through analytical and finite element methods’ by H. Li, 2013 [3]
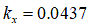 [m]
[m]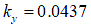 [m]
[m]
また、Wong[10]によると、収集した実験データに基づいて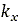 の値は、堅い砂地の0.01[m]から、ばら砂の0.025[m]にまでわたり、最大限圧縮した粘土質では約0.006[m]に達します。降り積もったままの新雪の場合、
の値は、堅い砂地の0.01[m]から、ばら砂の0.025[m]にまでわたり、最大限圧縮した粘土質では約0.006[m]に達します。降り積もったままの新雪の場合、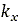 の値は0.025[m]から0.05[m]の範囲で変化します。
の値は0.025[m]から0.05[m]の範囲で変化します。
排土抵抗
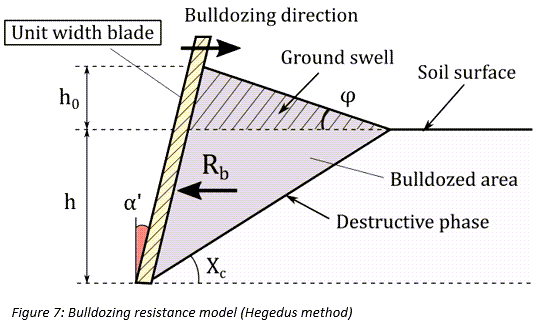
ホイールで土の質量を押しのけるときに排土抵抗が発生します。タイヤの沈下に起因する横力を考慮する場合は、接線応力に起因して接触パッチに働くせん断力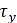 に、ホイール側面に作用する排土力を加算する必要があります。このタイヤモデルでは、排土力の計算にHegedus抵抗推測法[11]を使用しています。図7に示すように、ブレードが土の方向に移動するに伴い、ブレードの単位幅あたりで次の式による排土抵抗
に、ホイール側面に作用する排土力を加算する必要があります。このタイヤモデルでは、排土力の計算にHegedus抵抗推測法[11]を使用しています。図7に示すように、ブレードが土の方向に移動するに伴い、ブレードの単位幅あたりで次の式による排土抵抗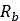 が発生します。
が発生します。
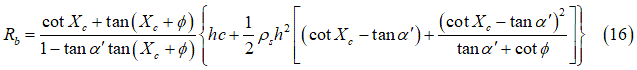
 は土の密度です。また、Bekker理論[12]に基づく崩壊角
は土の密度です。また、Bekker理論[12]に基づく崩壊角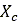 を次のように近似できます。
を次のように近似できます。
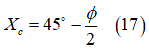
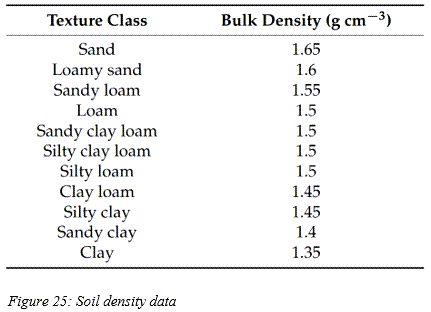
さまざまな土質クラスについて、土の密度の一般的な値を付録Aに示しています。
タイヤの変形能
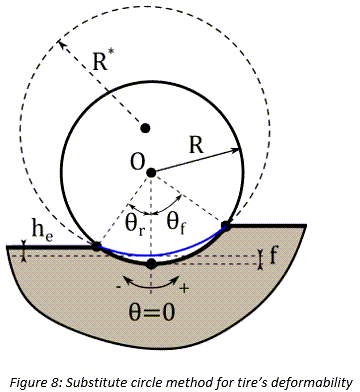
タイヤの変形能を考慮するために、図8に示すようにタイヤより大きい代用円を使用して、タイヤと土の間の接触パッチを記述します[1]、[4]、[13]。この代用円の直径を計算するには、土の垂直方向反力と垂直方向作用力が平衡状態になるまで繰り返し手順を実行します。垂直方向反力は、接触パッチ領域で法線方向とせん断方向の応力を積分して計算します。垂直方向作用力の計算では、タイヤの垂直方向剛性とタイヤのたわみを使用します。具体的には次のようになります。
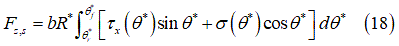
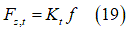
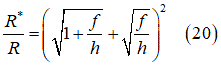
次の条件が成立するまで、上述の3つの式を繰り返し解きます。
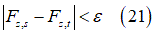
トレランス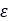 はタイヤの最大垂直方向荷重の関数です。タイヤの変形を無視できるのであれば、タイヤのパラメータファイルでブールフラグRIGID_MODE= 'TRUE'を設定することで、垂直方向の力
はタイヤの最大垂直方向荷重の関数です。タイヤの変形を無視できるのであれば、タイヤのパラメータファイルでブールフラグRIGID_MODE= 'TRUE'を設定することで、垂直方向の力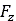 の計算を簡素化して演算時間を短縮できます。具体的には、計算の繰り返しが不要になります。式(18)の計算で、
の計算を簡素化して演算時間を短縮できます。具体的には、計算の繰り返しが不要になります。式(18)の計算で、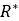 が
が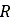 、
、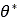 が
が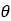 にそれぞれ置き換えられるからです。上記のブールフラグはデフォルトでFALSEに設定されているので、代用円の概念が使用され、高い精度が得られます。
にそれぞれ置き換えられるからです。上記のブールフラグはデフォルトでFALSEに設定されているので、代用円の概念が使用され、高い精度が得られます。
マルチパス効果
マルチパス効果では、繰り返し法線荷重に対する土の応答を確定する必要があります。具体的には、土が事前圧縮されている場合は、法線方向圧力分布の数学的記述を修正する必要があります。図9に示すように、初期の法線方向圧力分布は弾性部分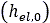 で構成されています。この部分は、そこを以前に通過したタイヤによって作成された弾性(無荷重)沈下量に等しくなります。続いて、圧力と沈下量との関係が式(1)に従って継続します。最終的に、無荷重弾性部分
で構成されています。この部分は、そこを以前に通過したタイヤによって作成された弾性(無荷重)沈下量に等しくなります。続いて、圧力と沈下量との関係が式(1)に従って継続します。最終的に、無荷重弾性部分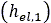 が発生します。
が発生します。
すでに触れたように、土に誘引される変形の一部は弾性(弾性沈下)で、残りの部分(塑性沈下)は非可逆性です。この弾性部分は次の式で求めることができます。
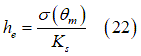
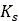 は土の弾性剛性です。
は土の弾性剛性です。
マルチパス効果が目的でなければ、路面データファイルでブールフラグMULTIPASS='FALSE'を設定してもかまいません。デフォルトでは、路面データを更新できるように、このフラグはTRUEに設定されています。
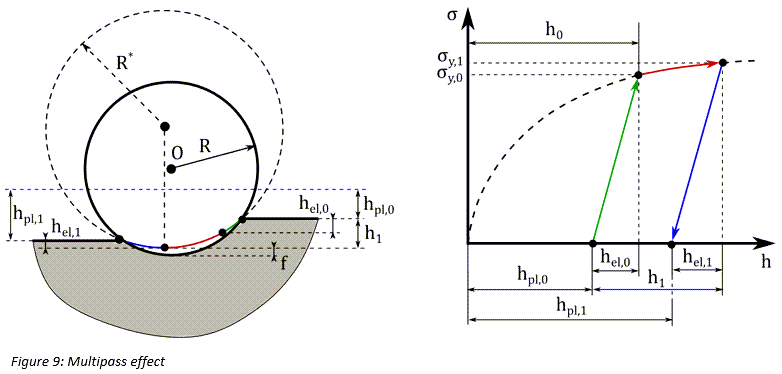
タイヤ力
縦力:
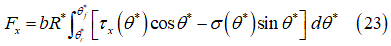
横力:
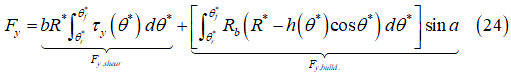
転倒モーメント:
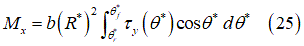
転がり抵抗モーメント:
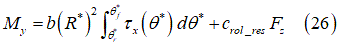
自己アライニングモーメント:
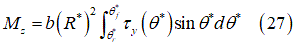
タイヤの変形能を考慮する場合に上記の式を使用します。RIGID_MODEフラグをTRUEに設定すると、量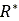 が
が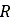 、量
、量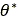 が
が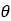 にそれぞれ置き換えられます。
にそれぞれ置き換えられます。
上記の各積分が数値計算される点に注目してください。路面データファイルのPARAMETERSブロックで整数の変数NODES=xと設定することで、これらの積分に使用されるポイントの数を変更して高精度な計算を実現できます。ほとんどの場合、積分ポイントを3~5個程度にすることで十分な精度が得られます。
路面モデリング
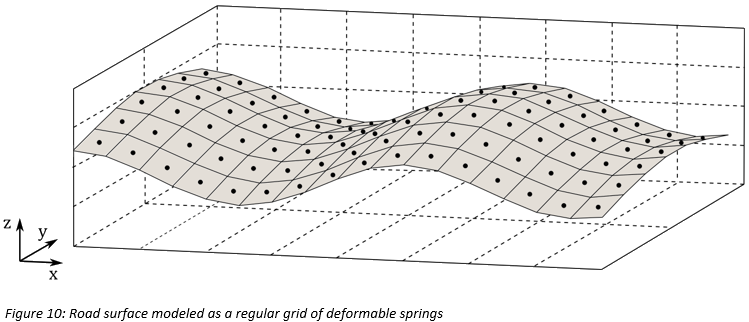
このタイヤモデルでは、図10のように、垂直方向(z軸方向)に変形できるスプリングで構成した規則的なグリッドとして路面を表現します。この手法では、各スプリングが小さい路面パッチを表現し、必要な情報をそこに保存できます。このような値として一般的なものに、土の各種パラメータ、土面の上昇量(z座標)、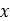 座標と
座標と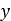 座標の関数とした土の圧縮
座標の関数とした土の圧縮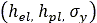 に関する情報などがあります。各領域に保存する情報は、他のスプリングから独立して設定できます。また、グリッドの間隔はモデルの最小タイヤ幅に基づいて自動的に設定されます。
に関する情報などがあります。各領域に保存する情報は、他のスプリングから独立して設定できます。また、グリッドの間隔はモデルの最小タイヤ幅に基づいて自動的に設定されます。
接触法
軟らかい土の上を走行するタイヤのモデルでは2種類の接触法を使用できます。両方の接触法で必要な出力は、土面の上昇量と路面の局部的な傾斜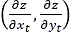 です。デフォルトの接触法は、接触パッチ領域に属するすべてのスプリング領域を収集し、平均化プロセスで土面上昇量の代表値を計算する方法です。この方法は、放射基底関数(RBF)補間によって実現できます。また、この方法を使用することで、路面の局部的な傾斜
です。デフォルトの接触法は、接触パッチ領域に属するすべてのスプリング領域を収集し、平均化プロセスで土面上昇量の代表値を計算する方法です。この方法は、放射基底関数(RBF)補間によって実現できます。また、この方法を使用することで、路面の局部的な傾斜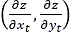 を効率的に計算できます[14]。
を効率的に計算できます[14]。
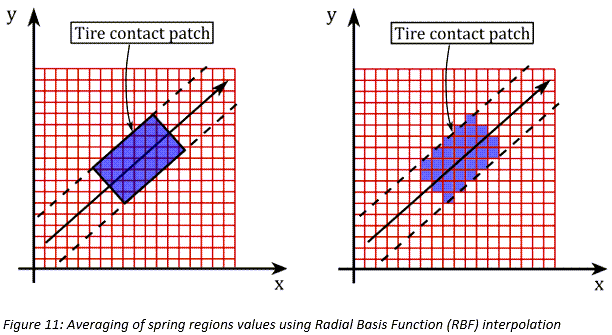
もう一つの方法は、3次元エンベロープ接触法です[15]、[16]。路面の高さが短い周期で変化する場合(急峻なステップ状で変化する場合)は、この接触法を使用することで高い精度が得られます。ただし、先に紹介したRBF補間法と比較すると、計算上の負荷が高くなります。この方法の中心的な概念は、一群の楕円を使用して路面プロファイルをスキャンし、3つの量で定義した実効的な路面を生成することです。この3つの量とは、修正した実効路面高さ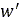 、実効前方傾斜
、実効前方傾斜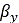 、実効路面キャンバー角
、実効路面キャンバー角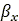 です。きわめて簡潔なこの接触モデルを図12に示します。このモデルでは3つの量が次のようになります:
です。きわめて簡潔なこの接触モデルを図12に示します。このモデルでは3つの量が次のようになります:
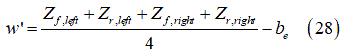
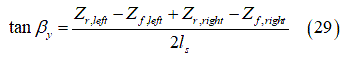
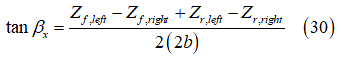
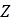 は楕円(カム)中心の高さです。
は楕円(カム)中心の高さです。
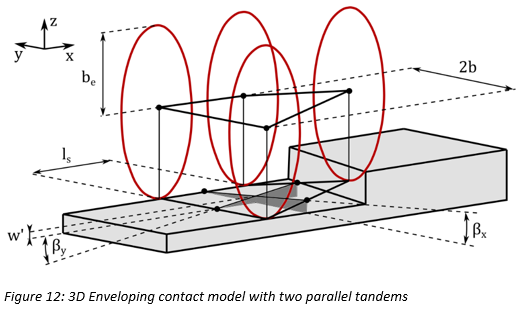
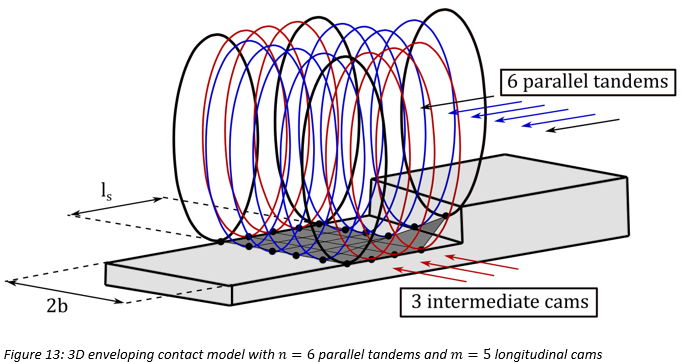
一般的に、急峻で不規則性がある路面で正確な結果を得るには、平行に配置したカム(タンデム)が2つでは不十分です。したがって、図13のように平行タンデムと中間カムを追加します。実効路面キャンバー角の計算では、左右カムの間の中間カムによる効果が相殺されるので、これらの中間カムは不要です[15]。前段の簡潔な包絡線接触モデルで紹介した式をここでも使用しますが、複数の平行タンデムと中間カムのモデルに使用できるように拡張します。具体的には次のようになります:
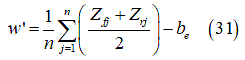
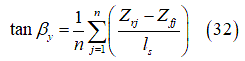
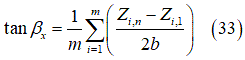
| パラメータ | 説明 | 単位 |
|---|---|---|
| PAE | 楕円の半値長さ / 無荷重半径 | - |
| PBE | 楕円の半値高さ / 無荷重半径 | - |
| PCE | 楕円の指数 | - |
| PLS | タンデムの基本長係数 | - |
| MAX_OBS_HEIGHT | 障害物の最大高さ | 長さ |
| N_WIDTH | 接触幅方向のカムの数 | - |
| N_LENGTH | 接触長さ方向のカムの数 | - |
| N_MESH | 楕円の離散化ポイントの数 | - |
複数のタイヤがある場合、どのタイヤで3次元エンベロープ接触法を使用するかを設定できる点に注目してください。つまり、放射基底関数(RBF)補間法を使用するタイヤと、3D包絡線接触モデルを使用するタイヤの両方が共存するモデルとして、精度と計算効率が両立する最適な組み合わせを見出すことができます。アプリケーションのニーズに応じてさまざまなタイヤパラメータファイルを使用することにより、この組み合わせを実現できます。
過渡モデル
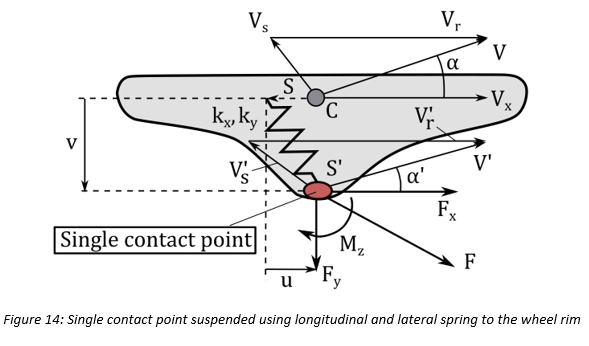
このタイヤモデルには、低速におけるその挙動を安定にするために、[16]で取り上げられている過渡モデルが組み込まれています。その中心となる考え方は、縦方向スプリングと横方向スプリングで接触点をホイールリムに結合することです。これらのスプリングは、タイヤのカーカスが持つコンプライアンスを表しています。具体的には、図14のように、これらのスプリングを使用して接触点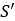 をホイールのスリップ点
をホイールのスリップ点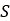 に結合し、このスリップ点をホイールリムに結合します。点
に結合し、このスリップ点をホイールリムに結合します。点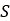 と点
と点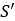 でのスリップ速度が異なることにより、カーカススプリングにたわみが発生します。これにより、縦方向たわみの時間導関数
でのスリップ速度が異なることにより、カーカススプリングにたわみが発生します。これにより、縦方向たわみの時間導関数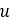 と横方向たわみの時間導関数
と横方向たわみの時間導関数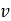 は次のようになります。
は次のようになります。
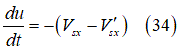
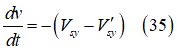
適切な変換[16]により、上記の常微分方程式(ODE)を次のように書き換えることができます。
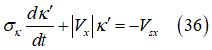
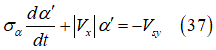
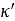 と
と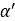 は接触パッチのスリップ量で、それぞれ
は接触パッチのスリップ量で、それぞれ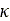 と
と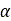 の代わりに使用されます。
の代わりに使用されます。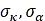 は縦方向と横方向の緩和長です。
は縦方向と横方向の緩和長です。
前進速度がゼロの状態で前記の式を使用すると、減衰しない振動が発生することが考えられるので、この過渡モデルには人工的な減衰が追加されています[16]。その場合、接触パッチの減衰スリップ量は次のようになります。
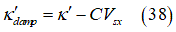
この式が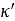 の代わりに使用されます。最終的に、この過渡モデルはスリップ特性の非線形範囲まで扱うように拡張されています。具体的には、制約を課した全面的に非線形なモデル[16]が導入されています。このモデルでも式(36)を適用しますが、緩和長を次の量に置き換えています。
の代わりに使用されます。最終的に、この過渡モデルはスリップ特性の非線形範囲まで扱うように拡張されています。具体的には、制約を課した全面的に非線形なモデル[16]が導入されています。このモデルでも式(36)を適用しますが、緩和長を次の量に置き換えています。
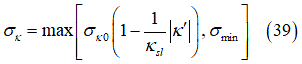
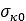 は
は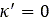 における緩和長の値、
における緩和長の値、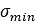 は数値的な問題を回避するために導入された最小緩和長の値、
は数値的な問題を回避するために導入された最小緩和長の値、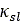 は最大の力が作用した場合のスリップ量の値です。式(38)と式(39)に類似した式は、接触パッチの横方向スリップ量
は最大の力が作用した場合のスリップ量の値です。式(38)と式(39)に類似した式は、接触パッチの横方向スリップ量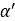 の計算でも適用しています。
の計算でも適用しています。
低速運転の状態ではソルバーが収束しないことが考えられます。その場合は、シミュレーションパラメータをデフォルト値から変更して解析を試します。具体的には、最大時間ステップを短くすることや最大次数を低くすることで問題を解決できる可能性があります。
静的
このタイヤモデルでは、垂直力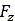 が縦方向スリップ長
が縦方向スリップ長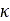 の値に依存します。したがって、初期の縦方向スリップが顕著な場合は、静的平衡位置を正確に計算するために、タイヤのパラメータファイルのINITIAL_VELOCITYブロックでタイヤの縦方向速度、横方向速度、回転速度の初期値を設定しておく必要があります。そのような状況ではない場合、これらの速度にはデフォルト値(ゼロ)を使用します。
の値に依存します。したがって、初期の縦方向スリップが顕著な場合は、静的平衡位置を正確に計算するために、タイヤのパラメータファイルのINITIAL_VELOCITYブロックでタイヤの縦方向速度、横方向速度、回転速度の初期値を設定しておく必要があります。そのような状況ではない場合、これらの速度にはデフォルト値(ゼロ)を使用します。

土壌ライブラリ
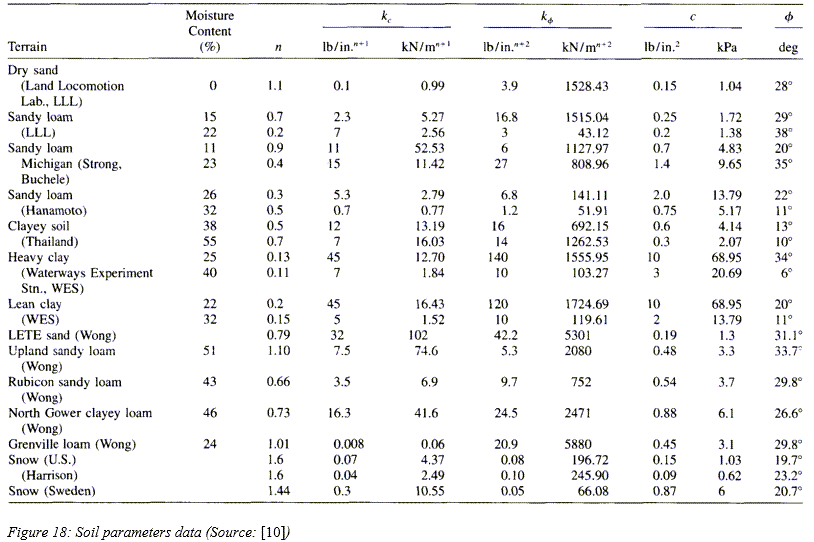
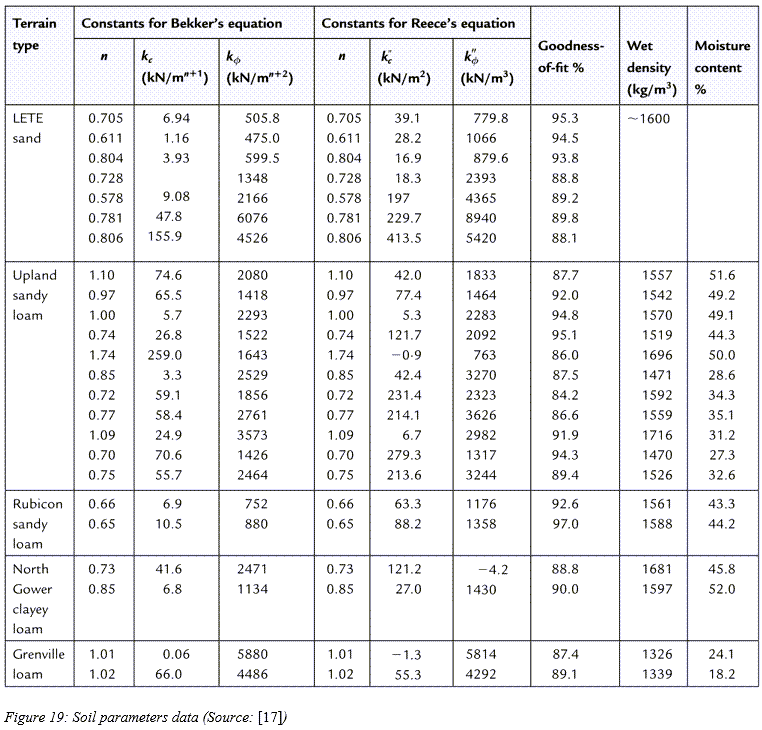
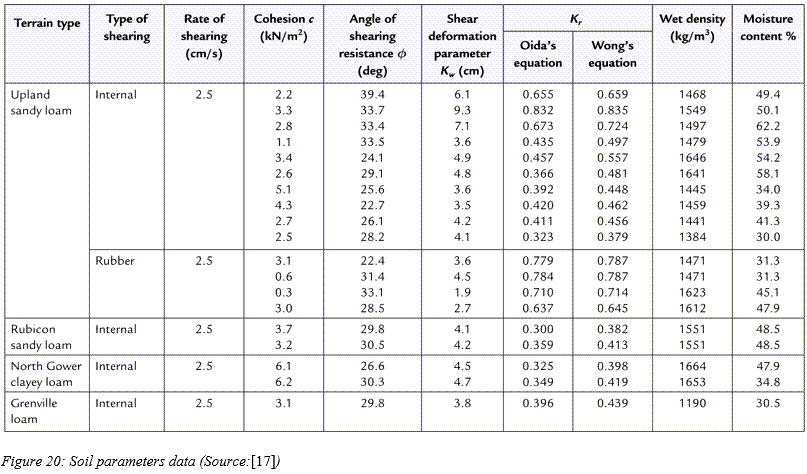
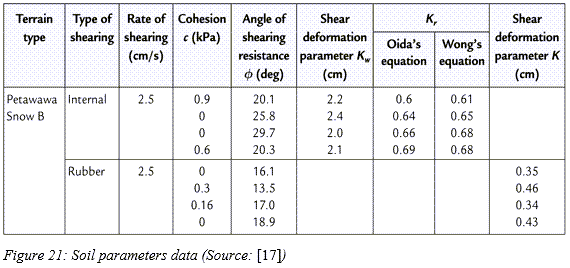
付録Aには、関連の書籍や論文を基にして、土の各種パラメータに関する大規模なデータベースが収録されています。また、多彩な土を取り上げているこのような参考資料に基づいて、すぐに使用できる路面データファイルを収めた土壌ライブラリが作成されています。この土壌ライブラリは、このソフトウェアのインストール環境にあります。
タイヤのパラメータ
- Unloaded radius
- Width
- 縦剛性
- タイヤの(内部)転がり抵抗係数
- 最大縦荷重
- 剛体モード(オプション。デフォルト=FALSE)
- 接触法(オプション。デフォルト=放射基底関数補間)
- 初速(オプション)
プロパティファイルの例
タイヤパラメータファイル

路面データファイル
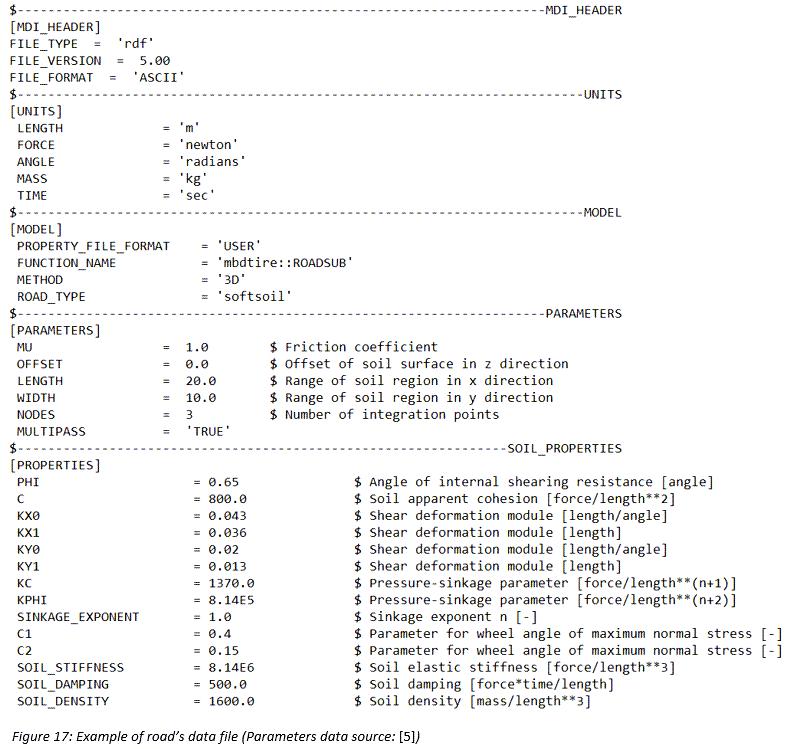
MotionSolveの出力要求
- F2 - 塑性沈下
- タイヤの動特性に起因する土の永久的な圧縮(図3の長さh-he)。
- F3 - 縦方向の抵抗
- 縦力に対する土の法線方向応力の寄与(式23をご参照ください)。
- F4 - 縦方向のせん断
- 縦力に対する土のせん断応力の寄与(式23をご参照ください)。
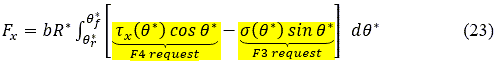
- F6 - 横方向の排土
- タイヤの横方向側面に作用する排土力(式24をご参照ください)。
- 横方向のせん断力
- 横方向の力に対する土のせん断応力の寄与(式24をご参照ください)。
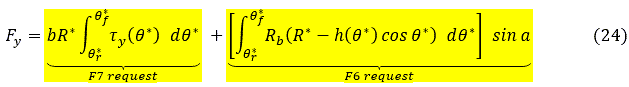
- F8 - タイヤの沈下
- タイヤの接触パッチにおける土の圧縮(図3の長さh)。
参考資料
[1] M.G.Bekker, Introduction to terrain-vehicle systems. part i: The terrain. part ii: The vehicle. Michigan Univ Ann Arbor, 1969.
[2] J.Y.Wong and A.R.Reece, “Prediction of rigid wheel performance based on the analysis of soil-wheel stresses Part I. Performance of driven rigid wheels,” J. Terramechanics, vol. 4, no. 1, pp. 81–98, 1967.
[3] Hao-Li, “Analysis of Off-Road Tire-Soil Interaction through Analytical and Finite Element Methods,” Technischen Universität Kaiserslautern, 2013.
[4] C. Harnisch, B. Lach, R. Jakobs, M. Troulis, and O. Nehls, “A new tyre-soil interaction model for vehicle simulation on deformable ground,” Veh. Syst. Dyn., vol. 43, no. SUPPL., pp. 384–394, 2005, doi: 10.1080/00423110500139981.
[5] I. Genya, M. Akiko, N. Keiji, and Y. Kazuya, “Terramechanics-Based Model for Steering Maneuver of Planetary Exploration Rovers on Loose Soil,” J. F. Robot., vol. 7, no. PART 1, pp. 81–86, 2015, doi: 10.1002/rob.
[6] Z.Janosi, “The analytical determination of drawbar pull as a function of slip for tracked vehicles in deformable soils,” in Proc. of 1st Int. Conf. of ISTVS, 1961.
[7] K. Yoshida and G. Ishigami, “Steering characteristics of a rigid wheel for exploration on loose soil,” 2004 IEEE/RSJ Int. Conf. Intell. Robot. Syst., vol. 4, no. January 2004, pp. 3995–4000, 2004, doi: 10.1109/iros.2004.1390039.
[8] A.Battiato, “Soil-tyre interaction analysis for agricultural tractors: modelling of traction performance and soil damage,” 2014.
[9] K. Yoshida, N. Mizuno, G. Ishigami, and A. Miwa, “Terramechanics-based analysis for slope climbing capability of a lunar/planetary rover,” in 24th Int. Symp. on Space Technology and Science, 2004.
[10] J.Y.Wong, Theory of ground vehicles. John Wiley & Sons, 2008.
[11] E.Hegedus, “A simplified method for the determination of bulldozing resistance,” 1960.
[12] M.G.Bekker, Off-the-road locomotion. The University of Michigan Press, 1960.
[13] I. C. Schmid, “Interaction of vehicle and terrain results from 10 years research at IKK,” J. Terramechanics, vol. 32, no. 1, pp. 3–26, 1995, doi: 10.1016/0022-4898(95)00005-L.
[14] N. Mai-Duy and T. Tran-Cong, “Approximation of function and its derivatives using radial basis function networks,” Appl. Math.Model., vol. 27, no. 3, pp. 197–220, 2003, doi: 10.1016/S0307-904X(02)00101-4.
[15] A.J.C.Schmeitz, “A semi-empirical three-dimensional model of the pneumatic tyre rolling over arbitrarily uneven road surfaces,” Delft University of Technology, 2004.
[16] H.B.Pacejka, Tire and Vehicle Dynamics. Elsevier, 2005.
[17] J.Y.Wong, Terramechanics and off-road vehicle engineering: terrain behaviour, off-road vehicle performance and design. Butterworth-heinemann, 2009.
付録A:土のパラメータの一般値