概要 / 例

説明

システムの特性の1つが、そのシステムで未知の変数の関数である場合、そのシステムは非線形と呼ばれます。以下に2つの例を示します。

例1（熱アプリケーション）

Steady State Thermalアプリケーションで有限要素法を使用して解かれる微分方程式は次のとおりです：

ここで：

• [k]は熱伝導率のテンソル
• qは熱源の出力の体積密度
• Tは温度（すなわち状態変数であり、システムの未知数です)

熱伝導率kが温度Tの関数である場合、システムは非線形システムです。

例2（磁気アプリケーション）

Magneto Staticアプリケーション（スカラーモデルを使用）で有限要素法を使用して解かれる微分方程式は次のように記述できます：

ここで：

• [μ]は計算ドメインでの透磁率のテンソル
• ϕは磁気スカラーポテンシャル（すなわち状態変数）
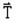• は供給源（印加された磁界源または電気ベクトルポテンシャル）に対応する項

透磁率μが磁界Hの関数である（すなわち状態変数ϕの関数である）場合、システムは非線形システムです。

例2： 基本（磁気アプリケーション）

Magneto Staticアプリケーション（ベクトルモデルを使用）で有限要素法を使用して解かれる微分方程式は次のように記述できます：

ここで：

• [ν]は計算ドメインでの磁気抵抗率のテンソル
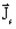• は電流源の密度
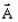• はベクトルポテンシャル（それぞれ状態変数、つまり、システムの未知数です）

磁気抵抗率νが磁束密度Bの関数である（すなわち状態変数Aの関数である）場合、システムは非線形システムです。

さまざまな可能性

Fluxアプリケーションでシステムが非線形と呼ばれるのは、次のような場合です：

• 材料の挙動則（構成方程式）が非線形である

  • B(H)非線形則：

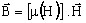
    （透磁率μは磁界Hの関数）

  • J(E)非線形則：

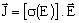
    （導電率σは電界Eの関数）

  • D(E)非線形則：

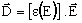
    （誘電率εは電界Eの関数）

• 熱特性が温度に依存している
  • 熱伝導率kはTの関数
  • 体積熱容量はTの関数
  • 熱交換係数はTの関数

Fluxでは

上記のモデルについては、材料： 基本の章で説明しています。