非線形システムの解析:ニュートン-ラフソン法
非線形システム: マトリックス形式の方程式
非線形システム(n個の方程式とn個の未知数)は次の形式で記述できます。
[A(X)].[X] = [B] (方程式1)
ここで、システムマトリックスAはベクトル解Xに依存します。
非線形システム: 解析
非線形システムの解は、反復法により、つまり、連立1次方程式のセットを解くことによって得られます。この解は、非線形システムの解に向かって収束します。
非線形システムを解析するためのさまざまな手法が存在しますが、解析プロセスの収束が保証されることはありません。Fluxで使用される方法は、ニュートン-ラフソン(NR)法です。この方法は、関数fの導関数f'(x)を計算可能な形式f(x) = 0の方程式に適用されます。
NR法について、次のパラグラフで簡単に説明します。
- “数値的アプローチ”より
- 例の“グラフィックアプローチ”より
NR法: 数値的アプローチ
ベクトルマトリックス関数の導入:[R(X)] = [A(X)].[X] - [B]
方程式1は次の形式で記述できます:[R(X)] = 0
NR法では、テイラー級数式からの反復法による関数R(X)が0の評価を行うことができます。
解かれるマトリックス方程式は、次の形式で記述されます:
![]()
ここで:
- dR/dXマトリックスはシステムのヤコビアン
- R(X)は残差ベクトル
各ステップで解の増分ΔXが計算されます。
ベクトル解は次のように記述されます:
![]()
基準εi < εに達すると、プロセスが停止します。ここで:
- εi = ||ΔXi+1||/||Xi+1||.
- εはユーザーが指定したニュートン-ラフソン手順の精度です。
NR法:グラフィックアプローチ(1)
接線法としても知られるニュートン-ラフソン法は、下の図の例の“グラフィックアプローチ”によって示されるようになりました。
例(Magneto Staticアプリケーション):
magneto staticアプリケーション(ベクトルモデルを使用)で有限要素法を使用して解かれる微分方程式は次の形式で記述されます:
![]() (方程式2)
(方程式2)
ここで:
- νは等方性計算ドメインの磁気抵抗率
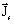 は電流源の密度
は電流源の密度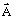 はベクトルポテンシャル(それぞれ状態変数、つまり、システムの未知数です)。
はベクトルポテンシャル(それぞれ状態変数、つまり、システムの未知数です)。
前提:
求める方程式2は、特性B(H)に対してH = Hsの場合の値Bを求めることと等価だと言えます。Hsは、電流源Jsによって発生する磁界です。
この方法のグラフィックアプローチ:
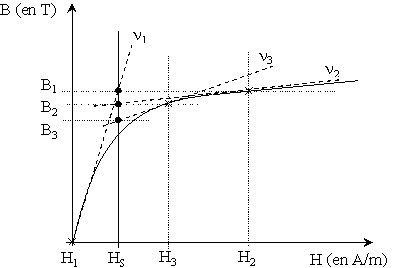
未知のBの最初の値を“任意”(0など)に選択し、曲線をその接線に置き換えます。そうすれば、接線の方程式(1次方程式)を使用して、Bの2つ目の値を簡単に計算し、2つ目の反復に進むことができます。逐次反復によって、必要なBの値に近づけることができます。
-
1回目の反復(原点で):B = 0、傾きν1の接線
接線に関連するB値の計算(H = Hsの場合のB) ⇒ B1
-
2回目の反復:B = B1、傾きν2の接線
接線に関連するB値の計算(H = Hsの場合のB) ⇒ B2
-
3回目の反復:B = B2、傾きν3の接線
接線に関連するB値の計算(H = Hsの場合のB) ⇒ B3 ...