ニュートン-ラフソン法のパラメータの調整

パラメータの調整

ニュートン-ラフソン法のパラメータとその使用方法は、信頼できる迅速な非線形解析を実現できるように自動的に設定されます。ただし、Solving process optionsボックスのNonlinear system solversタブを使用すると、これらのパラメータをユーザー側で調整できます。

ニュートン-ラフソン法による調整

以下のニュートン-ラフソン法パラメータを調整できます：

精度しきい値のタイプ：全体ベースの収束または変数ベースの収束。2Dと3Dヒステリシスプロジェクトを除き、安定化段階緩和法とSkew向け2D初期化を使用して最適な結果を得るために、変数ベースの収束が自動的に設定されます。これまでに、Skew向け2D初期化によって全体収束で高いパフォーマンスと優れた信頼性が得られています。これにより、系のすべての変数で目的の精度が確実に得られます。この場合、全体収束は収束が最も困難な変数に依存します。
しきい値：相対イプシロン値がこの値よりも低いと、ニュートン-ラフソン法の非線形ソルバーが停止します。緩和化または厳格化のどちらをアクティブにするかに応じて、このしきい値は固定値または適応条件手法の開始点になります。デフォルト値は10^-4です。
ニュートン-ラフソン法の最大反復回数：デフォルト値は100です。

容易な収束を検出するか困難な収束を検出するかに応じて適応条件手法が異なります。

図 1. 容易な収束（黄色）、通常の収束（緑）、困難な収束（赤）の図解
しきい値の緩和：この適応条件手法は、困難な収束を容易な収束にすることを目的としています。2回の連続したニュートン-ラフソン法反復で残差がどの程度減少したかに基づいて適応が決まります。
これら2つの反復での残差の減少比率がP（デフォルトは10%）よりも小さい場合は、収束が困難な状況であると考えられます（図1の赤色の領域）。収束が困難な状況である場合は、収束を容易にするために、このしきい値に係数F（デフォルト値は1.78）が乗算されます。
比率Pと係数Fは、次のようにアドバンストモードで変更できます。

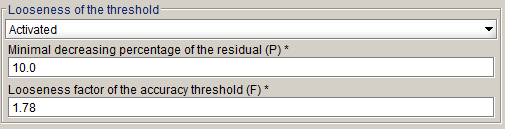
この手法は、2Dと3Dヒステリシスプロジェクト以外ではデフォルトでアクティブになっています。これにより、非線形プロジェクトの安定化段階緩和法とSkewの2D初期化で最良の結果が得られます。
しきい値の厳格化：この適応条件手法は、容易な収束を困難な収束にすることを目的としています。2回の連続したニュートン-ラフソン法反復で残差がどの程度減少したかに基づいて適応が決まります。
これら2つの反復での残差の減少比率がP（デフォルトは99%）よりも大きい場合は、収束が容易な状況であると考えられます（図1の黄色の領域）。収束が過度に容易である場合は、収束の難度を高くするために、このしきい値は係数F（デフォルトは3.16）で除算されます。
比率Pと係数Fは、次のようにアドバンストモードで変更できます。

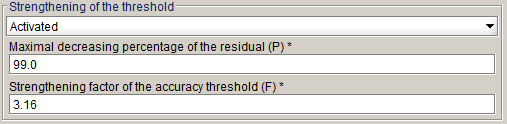
この手法は、2Dと3Dヒステリシスプロジェクト以外ではデフォルトでアクティブになっています。これにより、非線形プロジェクトの安定化段階緩和法とSkewの2D初期化で最良の結果が得られます。

緩和不足法（3D）

ニュートン-ラフソン法の緩和係数を定義するには、次の5つの手法があります：

階段法：ニュートン-ラフソン法アルゴリズムによって得られた精度で決まる簡単な法則に従って、ニュートン-ラフソン法の反復ごとに緩和係数が決まります。
固定法：解析プロセスを通じて一定値である緩和係数値をユーザーが入力します。
最適法：解析対象の非線形システムの残差を最小にすることにより、ニュートン-ラフソン法の反復ごとに緩和係数が決まります。
自動化法：定式化に応じ、プログラムによって“段階法”または“最適法”が自動的に選択されます。
最大係数法：解析対象の非線形システムの残差が減少するように、ニュートン-ラフソン法の反復ごとに最大の緩和係数が計算されます。

デフォルトで選択されている方法は自動化法です。これらの5つの方法について、以下で詳しく説明します。

階段法

ニュートン-ラフソン法の反復ごとに、以下の変数則に従い、その前の反復で取得した精度ε^i-1の値の関数として緩和係数が決まります。

最初の反復：

α = 0.5
次の反復：
- si ε^i-1 ∈ [0.1 ; +∞[ : α = 0.5
- si ε^i-1 ∈ [0.01 ; 0.1[ : α = 0.75
- si ε^i-1 ∈ [0 ; 0.01[ : α = 1

固定法

間隔]0 ; 1]の間にユーザーが緩和係数の値を入力します。したがって、この係数の値は解析プロセス全体を通じて変化しません。

最適法

反復ごとに緩和係数が決まります。この方法の原則は、次の目的関数が最小になるように、この係数を計算することです。

W^{i} = \sum_{j = 1}^{n} {(R_{j}^{i})}^{2}

ここで、 $R_{j}^{i}$ は、i番目の現在のニュートン-ラフソン法反復での残差R(Xⁱ)にあるj番目の成分です（R(Xⁱ)はn個の要素を持つベクトルです）。nは系の未知数の数です。

αの関数としてWを明示的に表現できないことから、反復法を使用して目的関数の最小値が検索されます。この検索は、

α = α_k = 1/2^k-1（α = 1 then 1/2, 1/4, 1/8...）の値に対するWiの値を計算することによって実行されます。反復k+1のWⁱ_k+1が前回の反復kのWⁱ_kよりも大きくなると、この検索は停止します。実際、一定の反復回数までは、α = α_k = 1/2^k-1は減少し、同時にWⁱ_kも減少しますが、その反復回数後は増加に転じます。

自動化法

領域に使用する定式化の関数がFlux 3Dによって自動的に決まり、これが最適な緩和手法になります。

Flux 3Dでは、この緩和手法として階段法が自動的に選択されます。ただし、磁気スカラーポテンシャル（減少値または合計値）に表面インピーダンス定式化ではない定式化を使用している領域では最適化法が使用されます。自動化法はデフォルトの方法です。

最大係数法

ニュートン-ラフソン法の反復ごとに緩和係数（α）を計算します。この方法では、非線形系の残差の減少基準に適合する範囲で最大の係数を検索します。そのためには、さまざまな値のαを使用して残差を計算します。まず、この係数を大きくした後（最大値は1）、非線形系の残差が前回のニュートン-ラフソン法反復で得られた値よりも大きい場合にのみ、この係数を小さくしていきます。

詳しくいうと、i番目のニュートン-ラフソン法反復では、前回のニュートン-ラフソン法反復で得られた緩和係数α（最初の反復ではα=1）からこの検索が始まります。つづいて、まずその係数（α = min(αφ,1)、φは黄金比）を大きくして非線形系の新しい残差を計算します。

その残差が前回のニュートン-ラフソン法反復の残差よりも小さい場合は、前回のニュートン-ラフソン法反復の残差よりも今回の残差が大きくなるか、大きくしたαが1に達するまで、同じ規則で係数を大きくしていきます。これにより、残差が小さくなった最後のα（最大値）を維持します。
この残差が、前回のニュートン-ラフソン法反復の残差よりも大きい場合は、その係数を小さくしてα = max(α/φ,β)とします。βは最小の緩和係数で、プロジェクトに応じて異なり、Fluxによって定義されます。それまでのニュートン-ラフソン法反復による残差のいずれかよりも今回の残差が小さい場合はその係数が維持されます。それ以外の場合は、同じ規則に従って係数を引き続き小さくしていきます。