等方性 / 異方性軟質材料: 解析飽和曲線 + 屈曲点調整
プレゼンテーション
このモデルは、飽和とそれに対応する屈曲点の制御を考慮して、等方性材料の非線形B(H)依存性を定義します。
数学モデル
このモデルは、前回と同様に、直線と曲線の組み合わせで構成されます。実験曲線に対する近似性が向上するように、屈曲点の形状を係数で調整できます。
対応する数式は次のように記述できます:
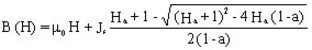
ただし、![]()
ここで:
- μ0は真空の透磁率、μ0 = 4 π 10-7 H/m
- µrは始点での材料の初期比透磁率
- Jsは飽和Tにおける磁気分極
-
aはB(H)曲線の屈曲点を調整する係数(0 < aおよびa < > 1)
この値が小さいほど曲線の曲がり方が急になります。
このB(H)モデルの形状は下図のとおりです。
異方性材料
異方性材料の場合、この線形モデルは3つの直線から成る1つのグループで構成されます。
このモデルは以下の条件で考慮されます:
- 2Dアプリケーション(2D平面領域):Magneto Static / Transient magnetic
- 領域: 磁性非導電性、ソリッド導体