Steady state AC Magneticアプリケーションでのモデルの近似

Steady state AC Magneticアプリケーションの留意事項

Fluxでは、Steady state AC Magneticアプリケーションにおいては、未知の状態変数と、導出された物理量である磁界強度および磁束密度は、時間依存の高調波（正弦波）を持つと想定されます。

複雑な表現が使用され、単一の解析プロセスで解を得ることができます。

生じる問題

Steady state AC Magneticアプリケーションでは、状態変数は正弦波の時間依存性を有し、磁界Hと磁束密度Bという量が導出されます。

あるいは実際に、磁界の計算ドメインに非線形磁気材料が含まれている場合、磁界Hと磁束密度Bが同時に正弦波の時間依存性を有することはできません（次の図をご参照ください）。

Bが正弦波の場合	Hが正弦波の場合

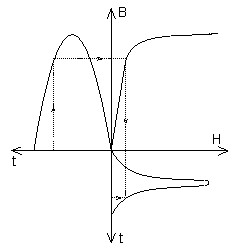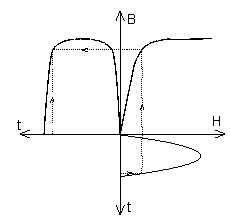… ⇒ Hは正弦波ではない	… ⇒ Bは正弦波ではない

提示される解

上記の矛盾を考慮するために、提示された磁化モデルで近似が実行されます。

磁気エネルギーの等価性に基づいた非線形磁化について、提示されたモデルを基準にして、B(H)の依存性の計算が変更されます。その後、エネルギー等価の法則による手法に基づいた等価なB(H)特性について説明します。

この手法の背後にある理論

エネルギーは、下図の網掛け部分に相当します。

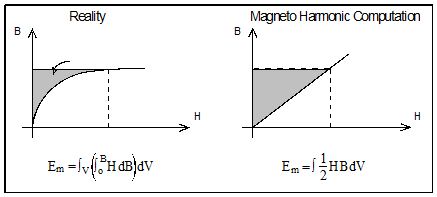
Steady state AC Magnetic計算の等価B(H)依存性は、実際のB(H)曲線から得られる磁界の経時変化の周期ごとの時間平均磁気エネルギーの密度が、等価B(H)依存性によって得られる磁気エネルギーの密度と等しくなるように計算されます。

等価B(H)依存性の計算については、下図に示す2つの極端なケースがあります。

Bが正弦波の場合	Hが正弦波の場合

実際の磁性状態(B_i, H_i)： B = B_iの場合、H = H_iとなります。等価値H_eqiは、等価エネルギーで動作するような、ポイント(H_i, B_i)からの水平変位によって得られます： B = B_iの場合、H = H_eqiとなります。量H_eqiは、網掛け部分同士が等しくなるように計算されます。	実際の磁性状態(H_i, B_i)： H = H_iの場合、B = B_iとなります。等価値B_eqiは、等価エネルギーで動作するような、ポイント(H_i, B_i)からの垂直変位によって得られます： H = H_iの場合、B = B_eqiとなります。量B_eqiは、網掛け部分同士が等しくなるように計算されます。

Bが正弦波の場合

Hが正弦波の場合

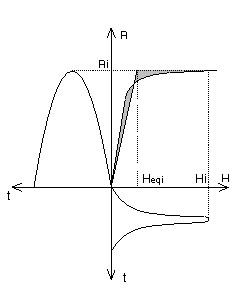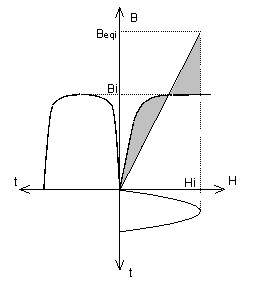
実際の磁性状態(B_i, H_i)：

B = B_iの場合、H = H_iとなります。

等価値H_eqiは、等価エネルギーで動作するような、ポイント(H_i, B_i)からの水平変位によって得られます：

B = B_iの場合、H = H_eqiとなります。

量H_eqiは、網掛け部分同士が等しくなるように計算されます。

実際の磁性状態(H_i, B_i)：

H = H_iの場合、B = B_iとなります。

等価値B_eqiは、等価エネルギーで動作するような、ポイント(H_i, B_i)からの垂直変位によって得られます：

H = H_iの場合、B = B_eqiとなります。

量B_eqiは、網掛け部分同士が等しくなるように計算されます。

この手法の背後にある理論（続き）

実際には、BもHも正弦波ではありません。上記の2つの極端なケースで計算される等価曲線によって得られる結果には、ほとんどの場合、正確な結果が含まれます。それは、これら2つの極端なケース間の線形組み合わせによって、等価曲線を等しく計算できるためです（Fluxで提供されている等価モデルをご参照ください）。

等価曲線

等価曲線を次の図に示します。

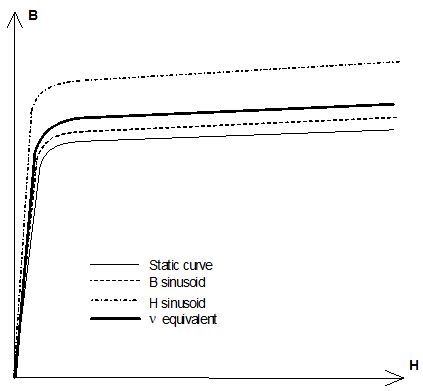
この手法の制限事項

すべてのケースで、エネルギーに依存するポスト処理済み量の数値のみが正しい値となります（力、電力、インダクタンスなど）。

瞬間量は正弦波形状で表されるため、これらの量は近似値です。そうであっても、これらの量から、ある程度正確な結果がわかります。

参考文献

Steady state AC Magneticにおける非線形磁気材料のモデル化に関する補足情報については、次のドキュメントをご参照ください：

“Contribution à la modélisation des moteurs asynchrones par la méthode des éléments finis”thesis of Eric VASSENT – 1990INPG (Contribution to the modelling of asynchronous motors by the finite elements method)
“Détermination des pertes par courant de Foucault dans les cuves de transformateursModélisation de régions minces et prise en compte de la saturation des matériaux magnétiques en régime harmonique”thesis of Christophe GUERIN – 1994INPG (Determining of eddy current losses in the transformers curves – Modeling of narrow regions and taking into consideration of magnetic materials in harmonic regime)
“Simulation of induction machine operation using complex magnetodynamic finite elements” by Eric VASSENT – IEEE Transactions on magnetics, vol. 25, No 4, July 1989

Fluxモデル

等価B(H)依存性用としてFluxで提供されているモデルを次の表に示します。

モデル	前提	等価B(H)曲線
未変更曲線		実際のB(H)
正弦波誘導	Bが正弦波の場合 B = B_msinωt	このモデルは、次のエネルギー等価関係に基づいています：このモデルは、電圧源を備えたデバイスのシミュレーションに対してより適しています。
正弦波のH界	Hが正弦波の場合 H = H_msinωt	このモデルは、次のエネルギー等価関係に基づいています：このモデルは、電流源を備えたデバイスのシミュレーションに対してより適しています。
混合		このモデルは、上記の2モデルの線形組み合わせです： B_eq = α.B_eqBsin +(1- α)B_eqHsin H_eq = α.H_eqBsin +(1- α)H_eqHsin ここで、αは0～1の範囲で経験的に選択された重み付け係数です。
一周期におけるνの平均	Bが正弦波の場合 B = B_msinωt	このモデルは、一周期における磁気抵抗率の平均を求めることで算出される等価磁気抵抗率ν_eqに依存しています：このモデルでは勾配µ₀の漸近線が存在しなくなるため、磁束密度の値が大きい場合は、他のモデルよりも精度が大幅に低くなります。