MV-3020：2自由度ばね質量システムの最適化

本チュートリアルでは、MotionSolveのOptimization Wizardを使って最適化問題をセットアップする方法について学習します。

MotionSolveは、システムレベルのシミュレーションを実行するために広く使用されています。一般的に、特定の設計の性能がどの程度優れているかを把握するためにシミュレーションを実行します。多くの場合、このようなシミュレーションの目標は、システムが目的の機能を最適な方法で実行できるようにする適切な設計パラメータ群を見出すことにあります。

一般に使用する設計変数は、各種コネクターの位置と方向、およびこれらのコネクターの力特性です。一部のボディの質量と材料のプロパティを設計変数とすることもあります。システムの挙動は通常、応答変数のセットで特徴づけられます。したがって、多くの場合、シミュレーションの目標は、望ましい値が応答変数に得られるような設計変数の値を見つけることになります。

以前は、このような解析では、モンテカルロシミュレーションや実験計画法などの技法が使用されていました。これらの手法はきわめて優れた機能を発揮しますが、計算量が多いため、多数のシミュレーションを必要とします。

MotionSolveは、設計感度を解析的に計算する機能を新たにサポートしています。設計感度は、設計変数を変数とする関数とした応答変数の偏導関数で構成するマトリックスです。勾配ベースの最適化エンジンは、これらの感度を使ってコスト関数を最小化することができます。このプロセスは設計最適化と呼ばれます。一部の設計問題の最適化を可能にする新しい最適化ツールキットも、MotionSolveで使用可能になりました。

設計感度に基づいた最適化は、統計的手法ほど一般的ではありませんが、これらの手法よりも大幅に高速であるため、多くの状況で推奨されるソリューションです。

本チュートリアルでは、以下について学習します：
  • MotionSolveでの最適化のプロセス
  • 設計変数としてのばね剛性の定義
  • 応答関数としての変位の定義
  • 目的関数としての応答の使用
  • 最適化の実行と結果のポスト処理
概要

2つのばねが連続して繋がれています。ばね1の剛性はk1、ばね2の剛性はk2です。ばね1の一端はグラウンドに固定されており、一方荷重P1がもう一端に作用しています。ばね2にはその一端にP2の荷重がかかっています。

解析の目的は、変位u1およびu2へのばねの剛性の感度を決定し、それらを使ってシステムのk1およびk2を特定または調整してu1とu2の特定の値を得ることです。

感度を計算するためのMotionSolveのDSA（Design Sensitivity Analysis： 設計感度解析）機能が、この例で活用されます。本チュートリアルでは、モデルを定義し実行するための手順をステップ毎に説明します。

図 1 は、問題のセットアップを示しています。この問題で使用されるプロパティも与えられています：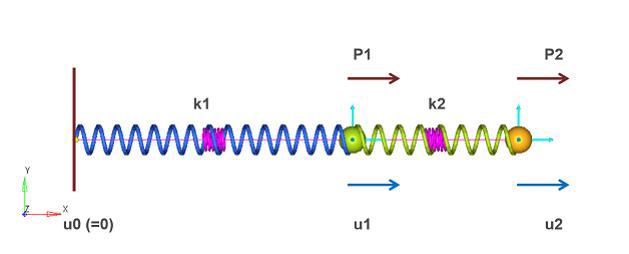


図 1. 連続して繋がれているばね – モデルの詳細
システムがフォローするプロパティのリスト：
  • 変位： u0 =0（固定）
  • Force:
    • P1 = 1N
    • P2 = 2N
  • 剛性：
    • k1 = 2 N/mm
    • k2 = 3 N/mm
  • 応答変数（RV）： u1およびu2
  • 設計変数（DV）： k1およびk2
  • Analysis Type：DSAを使用した静解析

最適化のプロセスは、MotionViewでのモデルのセットアップから始まります。MotionViewのOptimization Wizardを用いて、設計変数、応答および目的関数がセットアップできます。また、ウィザードを用いて、ユーザーが最適化を実行し、結果をプロット / 出力することもできます。さらなる解析のために、特定の反復計算からの設計を新規のMDLへとエクスポートすることも可能です。

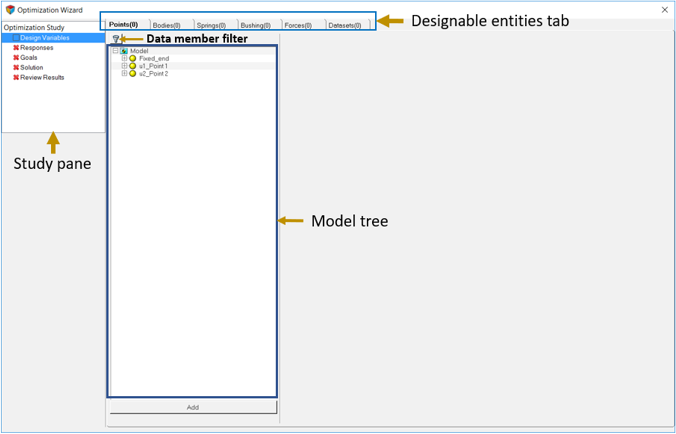
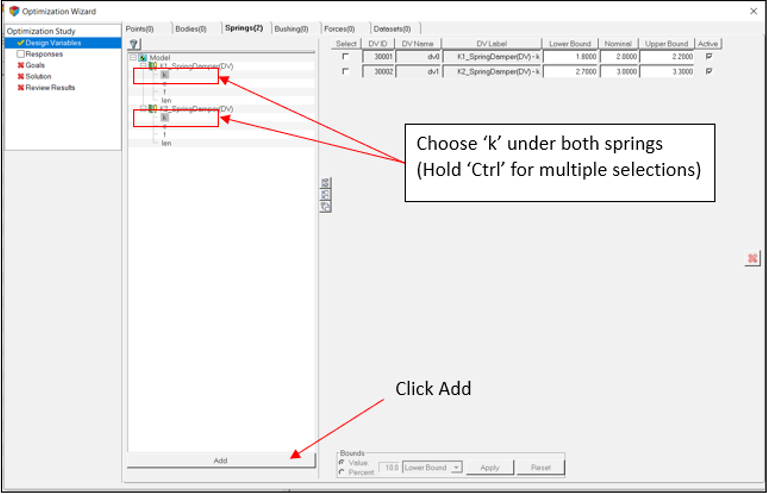
設計変数の追加

このステップでは、最適化のための設計変数を追加します。

開始に先立ち、mbd_modeling\motionsolve\optimization\MV-3020にあるmv_3020_initial_two_springs.mdlファイルを自身の<作業ディレクトリ>にコピーします。

  1. MotionSolveでmv_3020_initial_two_springs.mdlを開きます。
  2. ProjectブラウザでModelを右クリックし、コンテキストメニューからOptimization Wizardを選択します。
    Optimizationウィザードが表示されます。


    図 2.
    このウィザードでは、MotionSolveで最適化問題を解くための各手順が画面左のウィンドウで案内されています。本ウィザードは、設計変数を選択することができるDesign Variablesページがアクティブな状態で開きます。
  3. Design Variablesの下で、Springsタブをクリックします。
    2つのスプリングダンパーがリストされます：
    • K1_SpringDamper
    • K2_SpringDamper
    これらのばねのばね剛性は、設計変数として利用可能となっています。
  4. ‘+’ボタンをクリックし、2つのばねを展開します。
    設計可能とされているデータメンバーが図 3のように表示されます：


    図 3. 設計可能とされ得るばねデータメンバー
  5. Controlキーボードボタンを使って、両方のばねのk（剛性）データメンバーを選択します。モデルツリーの下部に用意されているAddボタンをクリックします。
    スプリングダンパーの剛性は、デフォルトの上限と下限を有した設計変数として追加されます。MotionSolveによって使用される境界値のデフォルト値は、初期値の10%です。
  6. 剛性の上限値と下限値を表 1に示すとおりに修正します：
    表 1.
    DV 下限値 上限値
    sd_0.k 0.25 4.0
    sd_1.k 0.25 4.0
    注: 上部のエンティティタブの括弧内の数値（この場合Springs(2)）は、そのエンティティタイプが定義される設計変数の数を示しています。
    これで、設計変数の定義が終わりました。

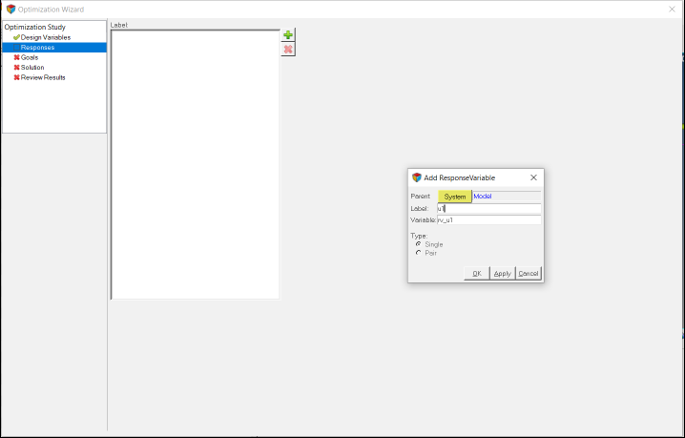
応答変数の追加

このステップでは、最適化のための応答変数を追加します。

この問題では、以下の2つの応答があります：
  • Displacement u1：u1が値3に達するよう、(1-u1/3)**2が使用されます。
  • Displacement u2：u2が値4に達するよう、(1-u2/4)**2が使用されます。

  1. Responsesページ上をクリックします。
  2. をクリックして、応答変数を追加します。表示されるダイアログ内で、Labelをu1に変更し、OKをクリックします。


    図 4. response1 u1の追加
    ResponseVariableが追加され、リストに表示されます。パネルも表示されます。
  3. このパネル内で、コンボボックスを使ってResponse TypeをGenericに変更します。
  4. スケール値として、デフォルトの1.0を使用します。
  5. Response Expressionキーに、以下の式を入力します：

    `(1-DM({b_0.cm.id},{m_0.id})/3)**2`

    ここで：

    b_0.cm.id = Body 0のCMマーカーのID

    m_0.id = u1_Point 1におけるグラウンドボディ上のマーカーのID

    注: 最適化の進行中、最適化エンジンは式全体を最小にするよう試み、DM({b_0.cm.id},{m_0.id})の値が3に近づくにつれて、この応答の値は最小化されます。
  6. Use derivativeチェックボックスをオンにします。
    チェックマークが入ると、シミュレーションの最終タイムステップにおいて計算される値が応答として使用されます。
  7. 上記のステップを繰り返し、もう1つのResponseVariable u2を以下の仕様で追加します。
    • Type = Generic
    • Response Expression = `(1- DM({b_1.cm.id},{m_1.id})/4)**2`
    これで、応答の追加が完了しました。

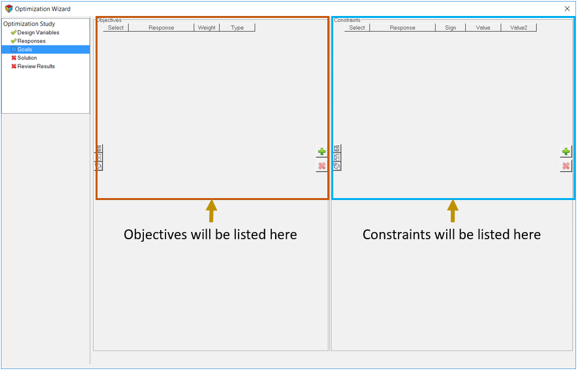
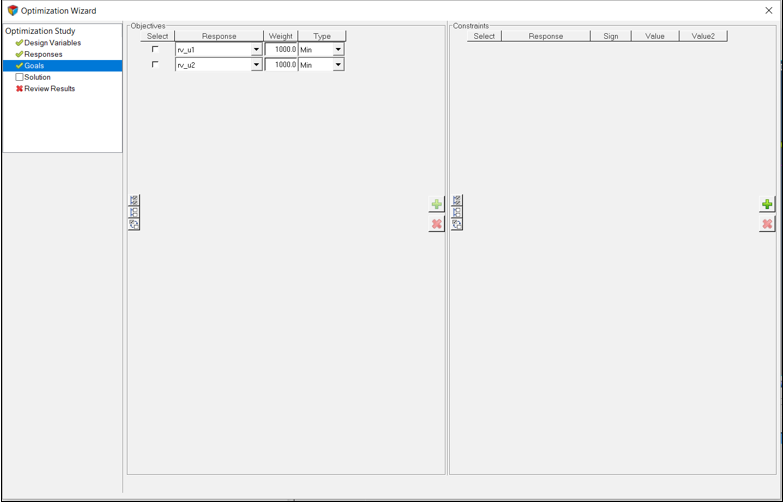
目的関数と制約条件の追加

ここで、2つの目的関数を問題に追加します。

目的関数は次のとおりです： 最適化の最後でu1の値は3、u2の値は4。この前のセクションで作成した応答を目的関数として使うことができます。

  1. Goalsページに進みます。
    このページには2つのセクション、ObjectivesとConstraintsがあります。


    図 5.
  2. Objectivesの下のボタンをクリックします。
    これで、応答rv_u1で目的関数が追加されます。
  3. Weightを1000に変更します。応答を最小限にするために、TypeはMinのままとします。
  4. ステップ2から3までを繰り返し、2つ目の目的関数（rv_u2）を作成します。


    図 6. 目的関数の定義
    この問題では、制約条件はありません。モデルのセットアップがこれで完了しました。

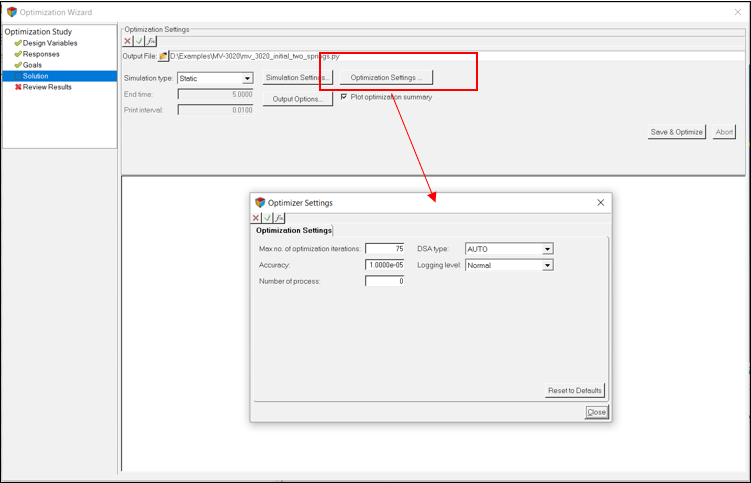
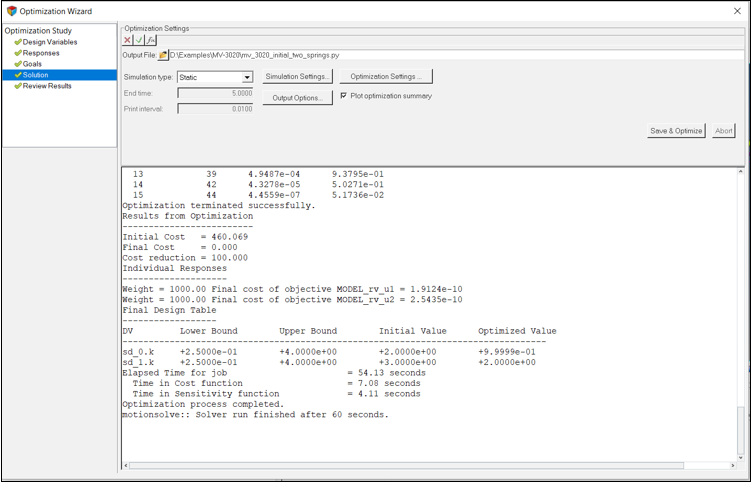
最適化の実行

このステップでは、最適化を実行します。

  1. Solutionsページに進み、最適化の設定を指定して解析を実行します。
    注: モデルは実行の前に保存されます。それが望ましくない場合は、最適化の開始前に異なるmdlファイル名で別名保存してください。これを行うには、一旦ウィザードを閉じてモデルを異なる名称で保存したうえで再度ウィザードを開く必要があります。
  2. Optimization Settingsボタンをクリックします。Optimizer Settingsダイアログで、Accuracyを1.0e-5に変更します。


    図 7. この問題のための最適化セットアップ
  3. その他のパラメータはデフォルト値のままとします。ダイアログを閉じます。
  4. Save & Optimizeをクリックして最適化を開始します。
    最適化が実行されている間、総加重コストvs.反復計算数のプロットと個々のコストvs.反復計算数のプロットが別々のウィンドウに表示されます（初期シミュレーション後）。

    最適化が完了すると、テキストウィンドウにサマリーがリストされます。

    注: 最適化の結果を見るには、一番下および / または右端までスクロールする必要があるかもしれません。
    テキストウィンドウは図 8のように表示されるはずです。


    図 8. 最適化完了後のテキストウィンドウ
    下のリストは、出力ウィンドウで得られる重要な情報を示しています：
    • 最適化エンジンの設定
    • 反復計算のサマリー - 反復計算番号毎のコスト関数の値
    • 最適化からの結果 - 初期コスト、最終コストおよびコストの低減パーセンテージ
    • 最適化後における各目的関数の最終値
    • 設計変数の上下限および初期値と設計変数の最適値についての情報を含んだ最終設計テーブル
    • コストと感度の計算のための経過時間

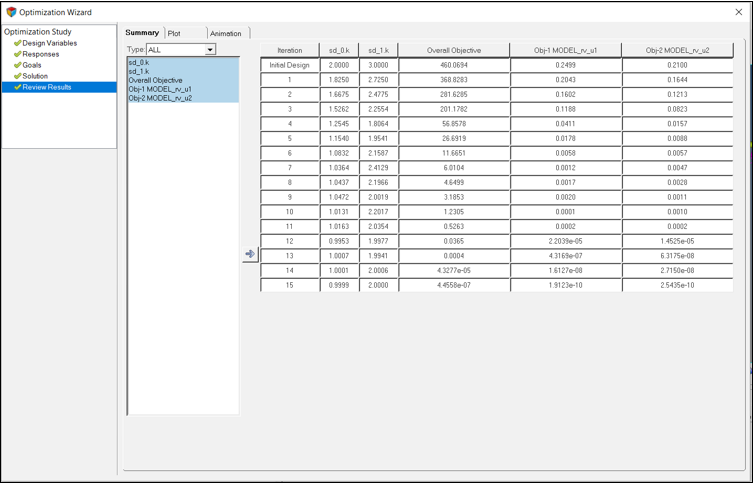
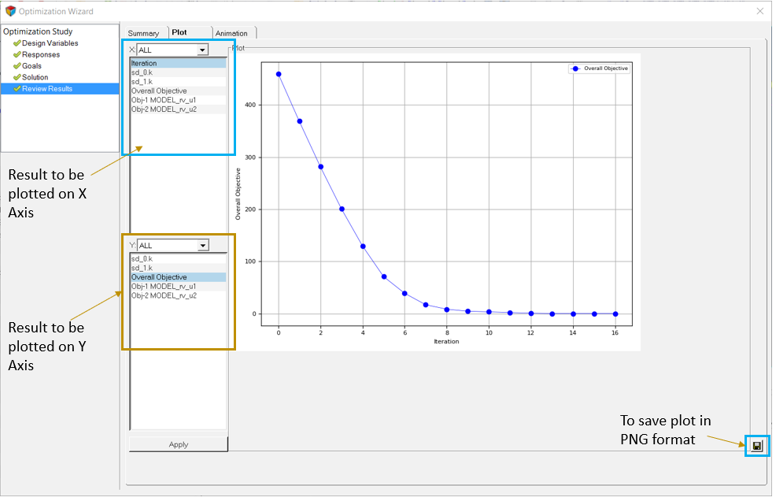
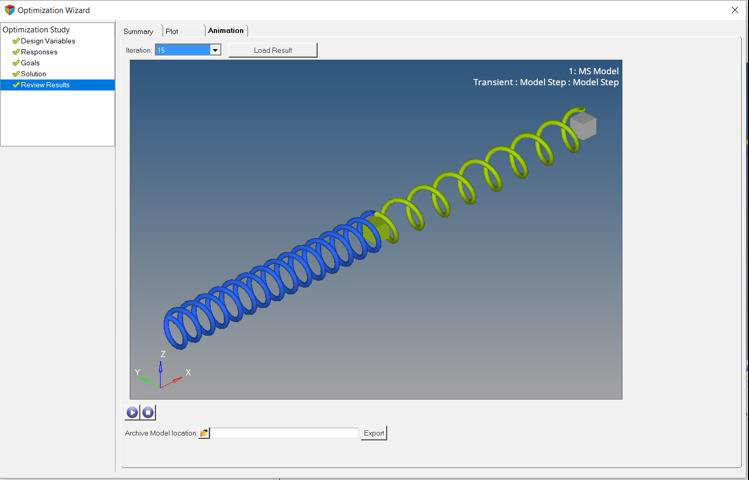
ポスト処理

このステップでは、最適化の結果をポスト処理します。

MotionViewは、最適化の結果をリスト、プロットおよびアニメーション表示する機能を提供します。また、任意の設計反復計算に対応するmdlモデルをエクスポートする機能も有しています。

  1. Review Resultsページに進みます。
    最適化ランの各反復計算について設計変数、応答および目的関数の履歴を表形式でリストしたSummaryタブが表示されます。
    注: MotionSolveは、最適化にSLSQPアルゴリズムを使用します。したがって、最終反復計算は通常、コスト関数が最小値となる最適なコンフィギュレーションとなります。図 9を参照してください。


    図 9. コスト関数（目的関数）、応答変数および設計変数をリストしたSummaryタブ
  2. Plotタブをクリックします。
    これは、設計変数、応答変数およびコスト関数の変動をグラフで可視化する助けとなります。ユーザーは、X軸の変数に対しY軸に任意の変数の数をプロットするよう選ぶことができます。


    図 10.
  3. XリストからIteration、YリストからOverall Objectiveを選択します。続いて、適用（Apply）をクリックします。
    注: Yリストから複数のアイテムを選んでプロットすることが可能です。
  4. Animationタブを選択し、反復計算中に生成されたコンフィギュレーションをアニメーション表示します。
  5. 最終反復計算（interation 16）からの結果ファイルを読み込みます。
    1. Iterationドロップダウンメニューから16を選択します。
    2. Load Resultをクリックします。
      アニメーションが表示領域に読み込まれます。
    3. （Play）をクリックします。
      これは統計解析であるため、アニメーションは1つのフレームのみを有しています。


      図 11. ‘Post Processing’ページのAnimationタブ
      このタブには、任意の反復計算からのモデルをMDL形式でエクスポートするためのArchive Model locationブラウザが用意されています。
  6. モデルをエクスポートします。
    1. ファイルパスを選択します。
    2. Exportをクリックします。
      これで、MDLおよびモデルを実行するためのその他の参照ファイル（存在する場合）を含んだアーカイブフォルダーが生成されます。設計変数値は、ユーザーが選択した反復計算番号の値に設定されます。