/MAT/LAW27 (PLAS_BRIT)

Block Format Keyword This law combines an isotropic elasto-plastic Johnson-Cook material model with an orthotropic brittle failure model. Material damage is accounted for prior to failure. Failure and damage occur only in tension. This law is applicable only for shells.

Format

(1)	(3)	(5)	(6)	(7)	(9)
/MAT/LAW27/`mat_ID`/`unit_ID` or /MAT/PLAS_BRIT/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$ $ρ_{i}$
`E`	$ν$ $ν$
`a`	`b`	`n`			$σ_{\max 0}$ $σ_{\max 0}$
`c`	${\dot{ε}}_{0}$ ${\dot{ε}}_{0}$	`ICC`	`F`_smooth	`F`_cut
$ε_{t 1}$ $ε_{t 1}$	$ε_{m 1}$ $ε_{m 1}$	`d`_max1		$ε_{f 1}$ $ε_{f 1}$
$ε_{_{t 2}}$ $ε_{_{t 2}}$	$ε_{m 2}$ $ε_{m 2}$	`d`_max2		$ε_{f 2}$ $ε_{f 2}$

Definitions

Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	Unit Identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$ $ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$ $[\frac{kg}{m^{3}}]$
`E`	Young's modulus. (Real)	$[Pa]$ $[Pa]$
$ν$ $ν$	Poisson's ratio. (Real)
`a`	Plasticity yield stress. (Real)	$[Pa]$ $[Pa]$
`b`	Plasticity hardening parameter. (Real)	$[Pa]$ $[Pa]$
`n`	Plasticity hardening exponent. (Real)
$σ_{\max 0}$ $σ_{\max 0}$	Plasticity maximum stress. Default = 10³⁰ (Real)	$[Pa]$ $[Pa]$
`c`	Strain rate coefficient. = 0 No strain rate effect. Default = 0.00 (Real)
${\dot{ε}}_{0}$ ${\dot{ε}}_{0}$	Reference strain rate. If $\dot{ε} \leq {\dot{ε}}_{0}$ $\dot{ε} \leq {\dot{ε}}_{0}$ , no strain rate effect. (Real)	$[\frac{1}{s}]$ $[\frac{1}{s}]$
`ICC`	Strain rate computation flag. 4 = 0 (Default) Set to 1. = 1 Strain rate effect on $σ_{\max}$ $σ_{\max}$ . = 2 No strain rate effect on $σ_{\max}$ $σ_{\max}$ . (Integer)
`F`_smooth	Strain rate smoothing flag. =0 (Default) Not active. =1 Active. (Integer)
`F`_cut	Cutoff frequency for strain rate smoothing. 5 Default = 10³⁰ (Real)	$[Hz]$ $[Hz]$
$ε_{t 1}$ $ε_{t 1}$	Tensile failure strain at which stress starts to reduce in the principal strain direction 1. 6 Default = 1.0 x 10³⁰ (Real)
$ε_{m 1}$ $ε_{m 1}$	Maximum tensile failure strain in principal strain direction 1 at which the stress in the element is set to a value dependent on `d`_max1. 6 Default = 1.1 x 10³⁰ (Real)
`d`_max1	Maximum damage factor in principal strain direction 1. 6 Default = 0.999 (Real)
$ε_{f 1}$ $ε_{f 1}$	Maximum tensile strain for element deletion in principal strain direction 1. 6 Default = 1.2 x 10³⁰ (Real)
$ε_{t 2}$ $ε_{t 2}$	Tensile failure strain at which stress starts to reduce in the principal strain direction 2. Default = 1.0 x 10³⁰ (Real)
$ε_{m 2}$ $ε_{m 2}$	Maximum tensile strain in principal strain direction 2 at which the stress in the element is set to a value dependent on `d`_max2. Default = 1.1 x 10³⁰ (Real)
`d`_max2	Maximum damage factor in principal strain direction 2. 6 Default = 0.999 (Real)
$ε_{f 2}$ $ε_{f 2}$	Maximum tensile strain for element deletion in principal strain direction 2. Default = 1.2 x 10³⁰ (Real)

Example (Aluminum)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                  Mg                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/PLAS_BRIT/1/1
Aluminum
#              RHO_I
               .0027                   
#                  E                  NU
               60400                 .33
#                  a                   b                   n                                SIG_max0
              90.266              223.14                .375                                     177
#                  c           EPS_DOT_0       ICC   Fsmooth               F_cut 
                   0                   0         0         0                   0
#             EPS_t1              EPS_m1              d_max1              EPS_f1
                 .16                 .72                .999                   1
#             EPS_t2              EPS_m2              d_max2              EPS_f2
                   0                   0                   0                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

In this model, the material behaves as a linear-elastic material when the equivalent stress is lower than the plastic yield stress. For higher stress values, the material behavior is plastic and the stress is calculated as.(1)
$σ = (a + b {ε_{p}}^{n}) (1 + c \ln \frac{\dot{ε}}{{\dot{ε}}_{0}})$ $σ = (a + b {ε_{p}}^{n}) (1 + c \ln \frac{\dot{ε}}{{\dot{ε}}_{0}})$

Where,

$ε_{p}$ $ε_{p}$

Plastic strain

$\dot{ε}$ $\dot{ε}$

Strain rate

The plasticity hardening exponent, n must be less than 1.
This law allows the modeling of material damage and brittle failure in two principal directions (1 and 2).
This law is only applicable to shell elements. It is compatible with Shell Property (/PROP/TYPE1) and Sandwich Shell Property (/PROP/TYPE11).

The ICC flag defines the effect of strain rate on the maximum material stress

σ_{\max}

$σ_{\max}$ . Figure 1 shows the value of

σ_{\max}

$σ_{\max}$ for the corresponding ICC flag.

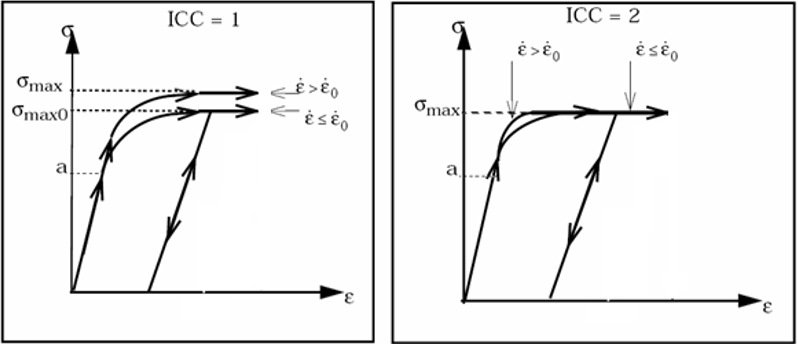
Strain rate smoothing is a process used to filter out higher strain rate frequencies.
When principal strain $ε_{i}$ $ε_{i}$ becomes higher than $ε_{t i}$ $ε_{t i}$ , then damage between $ε_{t i}$ $ε_{t i}$ and $ε_{f i}$ $ε_{f i}$ is controlled by the damage factor $d_{i}$ $d_{i}$ , which is given by the following equation.
$d_{i} = \min (\frac{ε_{i} - ε_{t i}}{ε_{m i} - ε_{t i}}, d_{\max}_{i})$ $d_{i} = \min (\frac{ε_{i} - ε_{t i}}{ε_{m i} - ε_{t i}}, d_{\max}_{i})$ in directions, $i$ $i$ = 1, 2.

Stress is reduced according to damage parameter $σ_{i}^{r e d u c e d} = σ_{i} (1 - d_{i})$ $σ_{i}^{r e d u c e d} = σ_{i} (1 - d_{i})$ . Damage is reversible between $ε_{t i}$ $ε_{t i}$ and $ε_{f i}$ $ε_{f i}$ . When $ε_{i} > ε_{f i}$ $ε_{i} > ε_{f i}$ , damage is set to $d_{\max i}$ $d_{\max i}$ and it is not updated further.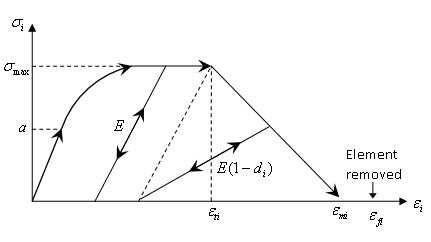

Figure 2.

$σ = (a + b {ε_{p}}^{n}) (1 + c \ln (\frac{\dot{ε}}{{\dot{ε}}_{o}}))$ $σ = (a + b {ε_{p}}^{n}) (1 + c \ln (\frac{\dot{ε}}{{\dot{ε}}_{o}}))$	$σ = (a + b {ε_{p}}^{n}) (1 + c \ln (\frac{\dot{ε}}{{\dot{ε}}_{o}}))$ $σ = (a + b {ε_{p}}^{n}) (1 + c \ln (\frac{\dot{ε}}{{\dot{ε}}_{o}}))$
$σ_{\max} = σ_{\max 0} (1 + c \ln (\frac{\dot{ε}}{{\dot{ε}}_{o}}))$ $σ_{\max} = σ_{\max 0} (1 + c \ln (\frac{\dot{ε}}{{\dot{ε}}_{o}}))$	$σ_{\max} = σ_{\max 0}$ $σ_{\max} = σ_{\max 0}$