TG Card
With the TG card, the already entered geometric elements (triangles, segments and the rest) can be translated, rotated, mirrored and/or scaled. It is also possible to duplicate structures.
On the Construct tab, in the Modify group,
click the ![]() Translate geometry (TG) icon.
Translate geometry (TG) icon.
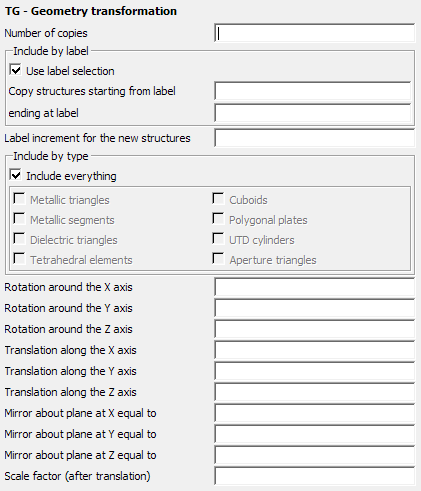
Figure 1. The TG - Geometry transformation dialog.
Parameters:
- Number of copies
- The number of copies to make, for example if set to 3 the selected elements will be rotated, translated, mirrored and scaled 3 times such that there will be a total of 4 structures. If set to 0, the existing elements, are rotated, translated, mirrored, scaled and the number of elements remains the same.
- Use label selection
- If this option is not checked, then the TG card applies to all the previously defined geometry. If this option is checked, then a label selective processing is possible.
- Copy structures starting from label
- Together with ending at label can be used to apply the TG card only to a selected part
of the structure. The TG card is applied only to those elements whose label lies within
the range set here (see also LA and CB cards and also the general discussion of label
ranges). If the second field is left empty, only structures with the label set in the
first field are considered. Note: That certain element types on the specified label(s) can be excluded from the selection lower in the card.
- Label increment for the new structures
- Each newly generated structure will be assigned a label that is incremented by this value from that of the original structure. An exception is the label 0 which is retained.
- Include
- This group can be used to specify which element types (provided they satisfy the label criterion) are rotated/translated.
- Rotation around the X axis
- Angle of rotation around the X axis in degrees.
- Rotation around the Y axis
- Angle of rotation around the Y axis in degrees.
- Rotation around the Z axis
- Angle of rotation around the Z axis in degrees.
- Translation along the X axis
- Translation in the X direction in metre (scaled by the SF card).
- Translation along the Y axis
- Translation in the Y direction in metre (scaled by the SF card).
- Translation along the Z axis
- Translation in the Z direction in metre (scaled by the SF card).
- Mirror about the plane at X equal to
- The geometry is mirrored around a plane at X equal to a constant specified. If no value is specified, no mirroring around the plane is performed.
- Mirror about the plane at Y equal to
- The geometry is mirrored around a plane at Y equal to a constant specified. If no value is specified, no mirroring around the plane is performed.
- Mirror about the plane at Z equal to
- The geometry is mirrored around a plane at Z equal to a constant specified. If no value is specified, no mirroring around the plane is performed.
- Scale factor
- The scaling factor
, with which the structures must be scaled. (If left empty,
it defaults to 1):
- For wire segments the wire radius is scaled as well as the coordinates of the start and end points.
- The scaling factor is applied after the translations/rotations have been conducted, for example, the new coordinates after the translation/rotation will be scaled. This means that the effective translation is the value specified at the TG card multiplied by the scaling factor. (If this is not desired, then two different TG cards may be used - the first applying only a scaling and the second performing the translation only).
When an SY card (symmetry) is used before the TG card, the TG card resets the symmetry if the new structures invalidates the symmetry. Cases where the symmetry is not reset is when, for example, the plane is a symmetry plane and the TG card specifies rotation about the Z axis for a symmetrical selection of elements. In this case the symmetry is retained.
Translation, rotation, mirroring and scaling are performed as a single transformation. The order is rotate, translate, scale and then mirror.
If more than one copy is made, successive points are generated from the previous point using the same relation.
With a TG card the simultaneous rotation around multiple axes as well as translation in multiple directions is possible. A point , for example the corner point of a triangle, is transformed to a new point
with the rotation matrix
Multiplication by the rotation matrix effectively rotates a point first by an angle around the Z axis, then by an angle around the Y axis and finally by an angle around X axis. It is important to note that the second rotation around the Y axis represents the global Y axis. This is also equivalent to rotating around the X axis, then rotating around the new axis and finally rotating around the new axis.
The transformation angles as used by Feko in this order are generally referred to as Kardan angles as opposed to the also commonly used Euler angles. If the rotation shall be performed in the other order (for example, first around the X axis, then around the Y axis and finally around the Z axis), then one can simply use multiple consecutive TG cards. But since the same rotation algorithm is also used at other Feko cards (for instance AC or AR) where one cannot use multiple cards, a short PREFEKO code segment shall be given here which illustrates how the angles can be converted:
** Desired rotation angles so that we rotate first around x, then y, and
** then around z
#a1=30 ** Angle in deg. around X axis
#b1=60 ** Angle in deg. around Y axis
#c1=90 ** Angle in deg. around Z axis
** Precompute sin() and cos() terms
#ca1=cos(rad(#a1))
#cb1=cos(rad(#b1))
#cc1=cos(rad(#c1))
#sa1=sin(rad(#a1))
#sb1=sin(rad(#b1))
#sc1=sin(rad(#c1))
** Auxiliary terms resulting from equating the transformation matrices
#cc2=#cb1*#cc1/(sqrt((#cb1*#cc1)^2+(#ca1*#sc1-#sa1*#sb1*#cc1)^2))
#cb2=#cb1*#cc1/#cc2
#ca2=#ca1*#cc2/#cc1
#sa2=#cc2*(#sa1*#cc1-#ca1*#sb1*#sc1)/(#cb1*#cc1)
#sb2=#sa1*#sc1+#ca1*#sb1*#cc1
#sc2=#cc2*(#ca1*#sc1-#sa1*#sb1*#cc1)/(#cb1*#cc1)
** Finally compute the angles which must be used in Feko in the TG card
** for the rotation order first around z, then around y, and then around x
#a2=deg(atan2(#sa2,#ca2))
#b2=deg(atan2(#sb2,#cb2))
#c2=deg(atan2(#sc2,#cc2))The file card based version of example_18.pre (see the Script Examples) gives an example of an application of the TG card.