1Vの一定電位における直線ワイヤの電荷分布。
Figure 5に示した基本的な八木-宇田アンテナは、いくつかの直線ワイヤで構成されています。1本の直線ワイヤの電荷分布の解析を検討します。このワイヤは長さが
、直径が2
aで、形状は
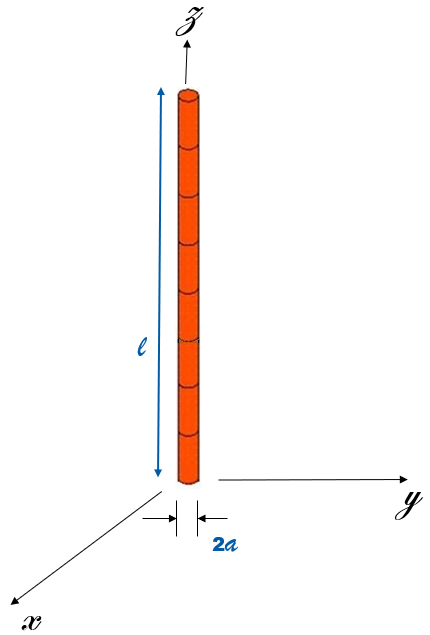
Figure 1に示すとおりです。
Figure 1. 一定電位に帯電したセグメント化直線ワイヤ。
1によると、線形の電荷分布
によって電位
が次のように作成されます。
(1)
ここで、
は給電源の座標、
rは観測座標、
は積分路、
Rは給電源上の任意のポイントから観測ポイントまでの距離です。これらの座標は次のように記述することもできます。
(2)
Note: Equation 1 はワイヤ上と自由空間で有効です。この問題では、これはいわゆる“境界条件”です。
一般的に任意の形状を持つ物体上の電荷分布は未知ですが、MoMの概要を理解するうえで、この直線ワイヤの例は効果的です。
このワイヤが1Vの一定電位に帯電しているものとします。簡潔にするために、このワイヤをZ 軸と平行に配置します。コンピューターでEquation 1を解くために、このワイヤを小さいセグメントに分割すると電荷分布を次のように近似できます。
(3)
一般的に基底関数と呼ばれる関数
は、未知の数量(ここでは、ワイヤセグメント上の電荷)の正確なモデル化と高い演算効率の実現を目的として選択されています。簡単にするために、各セグメントでは関数値が定数であると仮定します。具体的には、各
関数の値が、1つのセグメントでのみ1で、他のすべてのセグメントではゼロであるとします。関数値を定数とするこの仮定が成立するには、セグメントが十分に短いことが必要です。
Note: 目安として、セグメントの長さを波長の
とします。
したがって、Equation 1を次の式で近似できます。
(4)
Figure 5のように、ワイヤを
N個の一様なセグメントに分割し、各セグメントの長さを
とします。
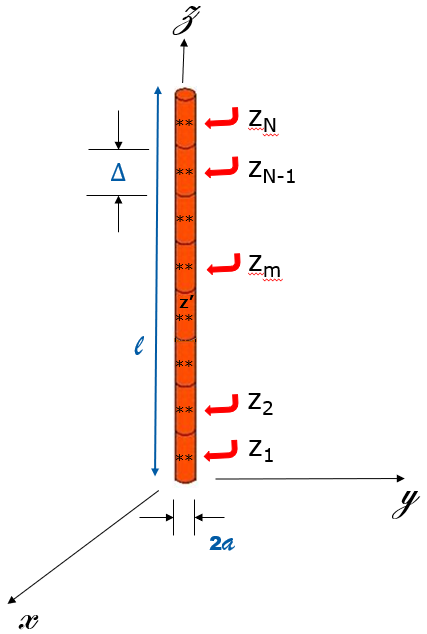
Figure 2. 一定電位に帯電したセグメント化直線ワイヤ。
どのl'の位置でもEquation 1が成立するので、半径aのワイヤセグメント上の固定ポイントzmをzの位置として選択できます。このように選択することで、Equation 4をz'のみの関数に簡素化して積分を計算できます。さらに、ワイヤをN個のセグメントに分割しているので、次のようにEquation 4をN個の未知数(an)を持つ1つの方程式に書き換えることができます。
(5)
N個の未知数を持つ1つの方程式では
N個の方程式が必要ですが、それぞれの方程式は線形で、他の方程式から互いに独立しています。これらの
N個の方程式を作成するには、長さが
の各セグメントの中央で観測ポイントzmを
Figure 2のように選択します。
Note: 観測ポイントを選択するこの作業を、
のテストまたはサンプリングと呼び、この手法を“点整合”または“コロケーション”と呼びます。
ポイントを
N回選択することで、
Equation 5は次のように簡約化できます。
(6)
Equation 6 は、行列の形式を使用して次のように簡潔な記述にすることができます。
(7)
Equation 7の各Zmn項は次のように記述できます。
(8)
また、残る2つの項は次のように記述できます。
(9)
(10)
Vm行列は1つの行と
N個の列で構成され、そのすべてのエントリは
に等しくなります。
anの値は、電荷分布の未知の係数です。
Equation 7を解くには、次のようにこの行列の逆行列が必要です。
(11)
Note: 広く知られていて、演算負荷も少ない逆行列手順であるLU分解に従います。この行列を、上三角行列と下三角行列に因数分解します。つづいて、ガウス消去法に類似の処理に従い、これらの行列を解きます。
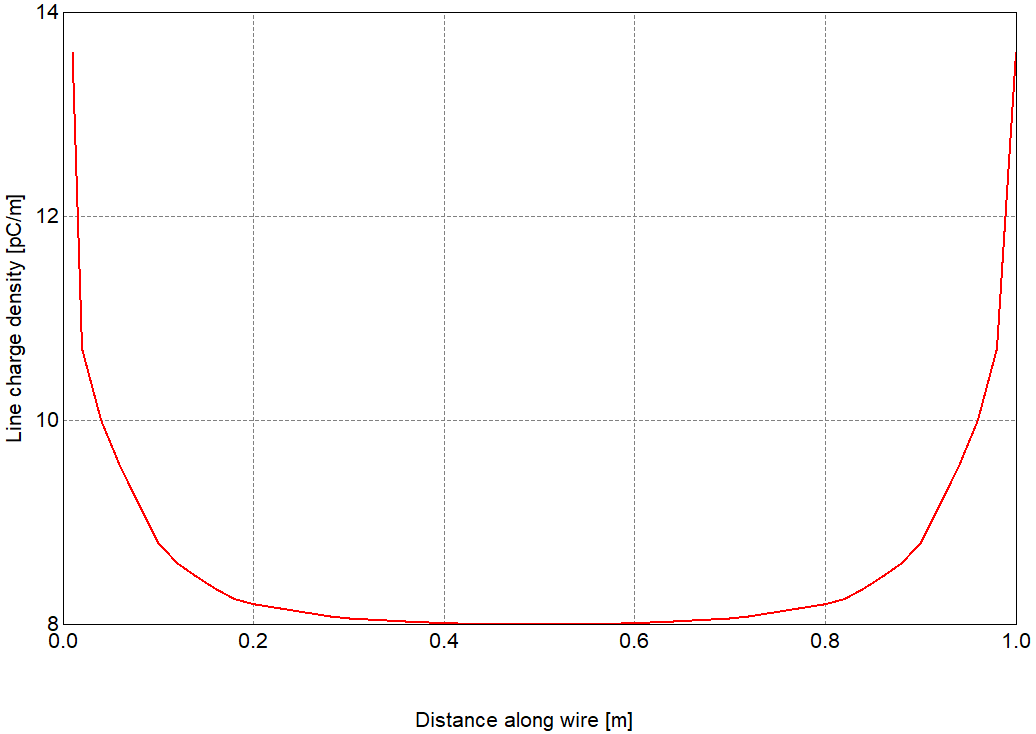
Figure 3 は、50個のセグメントに離散化した長さ1mのワイヤの線電荷密度を示しています。
Figure 3. 1Vの電位に帯電した直線ワイヤの線電荷密度。
問題が複雑になると、ここで示したように積分を近似式に簡約化できなくなります。