/MAT/LAW10 (DPRAG1)

降伏基準は圧力依存です。圧力を計算するには、状態方程式が与えられる必要があります（/EOS/COMPACTIONなど）。この材料則はソリッド要素とのみ適合性があります。

重要: バージョン2022より、この材料則から状態方程式（EOS）パラメータが削除されました。EOSパラメータを含む旧フォーマットを用いたモデルは、関連する/EOS/COMPACTIONと共に更新された材料則へのインポート中に変換されます。

フォーマット

(1)	(3)	(5)	(7)
/MAT/LAW10/`mat_ID`/`unit_ID`または/MAT/DPRAG1/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`	$ν$
`A`₀	`A`₁	`A`₂	`A`_max
$Δ P_{\min}$

定義

フィールド	内容	SI単位の例
`mat_ID`	材料識別子（整数、最大10桁）
`unit_ID`	単位識別子（整数、最大10桁）
`mat_title`	材料のタイトル（文字、最大100文字）
$ρ_{i}$	初期密度（実数）	$[\frac{kg}{m^{3}}]$
`E`	ヤング率（実数）	$[Pa]$
$ν$	ポアソン比（実数）
`A`₀	降伏基準係数（実数）	$[P a^{2}]$
`A`₁	降伏基準係数（実数）	$[Pa]$
`A`₂	降伏基準係数（実数）
`A`_max	降伏基準制限（フォンミーゼス制限）（実数）	$[P a^{2}]$
$Δ P_{\min}$	最小圧力デフォルト = -10³⁰（実数）	$[Pa]$

例（コンクリート）

#RADIOSS STARTER
/UNIT/1
unit for mat
                   g                  cm                 mus
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW10/1/1
Concrete
#              RHO_I
                 2.4                   
#                  E                  Nu
                .576                 .25
#                 A0                  A1                  A2                Amax
            9.72E-10             4.32E-5                 .48                .013
#              P_min 
              -1E-20 
/EOS/COMPACTION/1/1
Concreate EOS
#                 C0                  C1                  C2                  C3
                 0.0               0.256               0.256                   1
#              MUMIN               MUMAX                BUNL
                 0.0                0.44               0.115
#                PSH                RHO0
                   0                2.40  
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA

元のDrücker-Prager降伏基準は、線形圧力依存を有します。

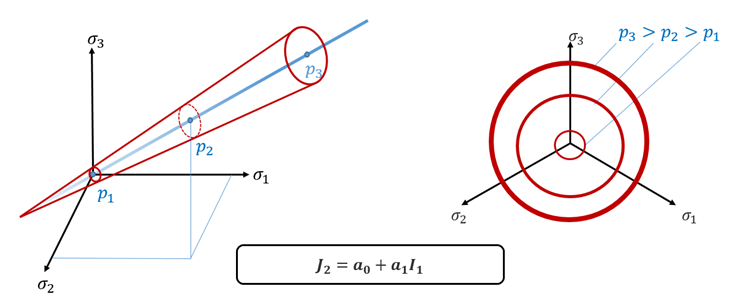
図 1. 元のDrücker-Prager降伏基準

Radiossは、その圧力依存が非線形である拡張Drücker-Prager降伏基準を使用しています。

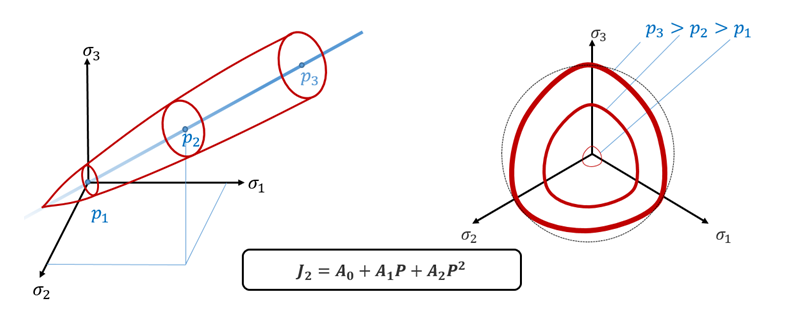
図 2. Radiossに組み込まれている拡張Drücker-Prager降伏基準
拡張Drücker-Prager降伏基準は、Mohr-Coulomb基準と比較され得ます。

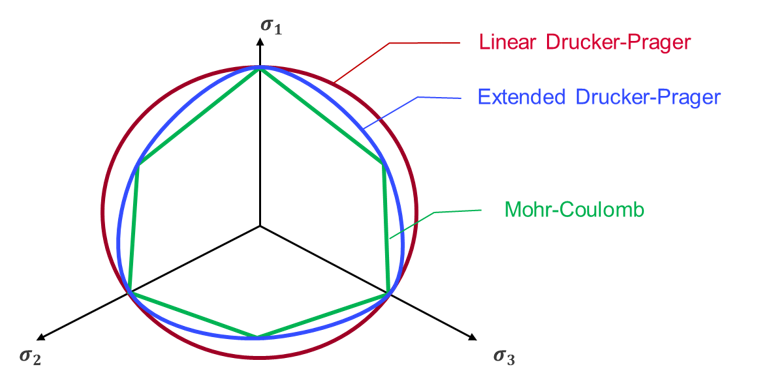
図 3. Radiossに組み込まれている拡張Drücker-Prager降伏基準 vs. Mohr-Coulomb基準

拡張Drücker-Prager降伏基準は、Mohr-Coulomb基準からフィッティングされ得ます。

$c$

粘着パラメータ

$ϕ$

内部摩擦の角度

この目的のために、パラメータ $A_{0}, A_{1}, A_{2}$ が次のように定義されなければなりません：(1)
$A_{0} = k {(c, ϕ)}^{2}$

$A_{1} = 6 k (c, ϕ) \times α (ϕ)$

$A_{2} = 9 α {(ϕ)}^{2}$

モデリングタイプ

パラメータ

外接Drücker-Prager基準

$\begin{array}{l} k = \frac{6 c \times \cos (ϕ)}{\sqrt{3} (3 - \sin (ϕ))} \\ α = \frac{2 \sin (ϕ)}{\sqrt{3} (3 - \sin (ϕ))} \end{array}$

中央円

$\begin{array}{l} k = \frac{6 c \times \cos (ϕ)}{\sqrt{3} (3 + \sin (ϕ))} \\ α = \frac{2 \sin (ϕ)}{\sqrt{3} (3 + \sin (ϕ))} \end{array}$

内接Drücker-Prager基準

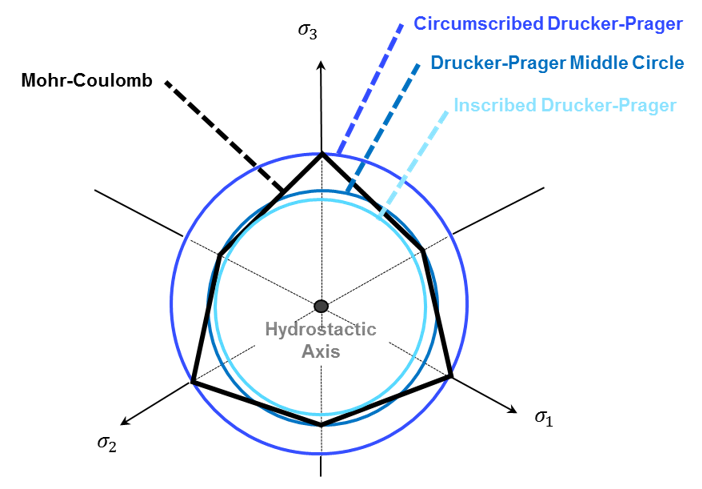
$\begin{array}{l} k = \frac{3 c \times \cos (ϕ)}{\sqrt{9 + 3 \sin^{2} (ϕ)}} \\ α = \frac{\sin (ϕ)}{\sqrt{9 + 3 \sin^{2} (ϕ)}} \end{array}$

図 4. Mohr-Coulomb基準（黒色）からDrücker-Prager降伏基準（青色）をフィッティング
/MAT/LAW21もまた拡張Drücker-Prager降伏基準をベースとしていますが、圧力の変化はユーザー関数で描写されることが可能です。
ヤング率Eとポアソン比 $ν$ は、ソリッド材料での音速計算に必要とされるせん断係数Gの決定に使用されます。

/MAT/LAW10 (DPRAG1)

フォーマット

定義

例（コンクリート）

コメント