Spectrum analysis (FFT)
Introduction
The user can represent the result of decomposition of the functions of spatial quantities or input/output parameters into Fourier series.
The results are obtained starting from the Fast Fourier Transform method.
Operation
The spectrums are generated in the following manner:
| Stage | Description |
|---|---|
| 1 | The user applies the Spectrum Analysis (FFT) command to an elementary curve of the 2D curve entity |
| 2 | The function to be analyzed is extrapolated over a full period by using the appropriate property of symmetry |
| 3 | The extrapolated function is decomposed into Fourier series by the Fast Fourier Transform method. The spectrum which represents the characteristics of various harmonics (amplitude, phase and order) is displayed. |
| 4 |
Two new 2D curve entities are created:
|
Principle
The spectral analysis is carried out in two phases:
- first, the function of spatial quantities or input/output parameters is extrapolated over a full period and the corresponding curve is plotted.
- second, the spectrum is generated by applying the Fast Fourier Transform method to the extrapolated function.
Given a curve representing the function f(x), the calculation of the coefficients of the Fourier Transform is performed as follows:
![]() ;
; ![]()
where:
- T is the period of the fundamental signal
- k is the order of the harmonic taken into consideration, k = 0, n
- This analysis uses the FFT algorithm, which is based on the partition with constant step in 2n+1 points, 2n-1-1 being the number of harmonics.
Periodic function: reminder
A periodic function
- can be presented by the Fourier series:
-

- comprises 3 elements:
- a constant a0, named DC component
- a fundamental characterized by the values a1 and b1,
- harmonics of order n >1 ( fractions of the fundamental period ) characterized by the value of the other Fourier coefficients an and bn.
Extrapolation of the curve
The spectrum analysis is performed over a full period. If the studied interval corresponds to a portion of the period, then the curve is extrapolated taking into consideration a full period.
The curve is extrapolated over a full period by copying repeatedly a portion of the period at regular intervals.
The types of extrapolation provided by Flux are dependent on the initial interval taken into consideration; they are presented in the table below and explained in greater detail in the following tables.
| Part of the represented period | Type of extrapolation |
|---|---|
| full period |
|
| half-period |
|
| a quarter of a period |
|
Example (1)
The extrapolation of a curve from a half-period is presented in the table below.
| Type of extrapolation | Formula | Image |
|---|---|---|
| normal symmetry | f(T/2+t)=-f(t) | |
| even symmetry | f(T/2+t)=f(T/2-t) | |
| odd symmetry | f(T/2+t)=-f(T/2-t) |
Example (2)
The extrapolation of a curve from a quarter of a period is presented in the table below.
| Type of extrapolation | Formula | Image |
|---|---|---|
| even symmetry | f(T/4+t)=f(T/4-t), f(T/2+t)=-f(t) | |
| odd symmetry | f(T/4+t)=-f(T/4-t), f(T/2+t)=f(t) |
|
Decibel mode
The spectrum of amplitudes is presented in linear mode and in decibel mode. The decibel mode intensifies the quantities in an exponential manner and enables us to see the differences that are not perceptible in linear mode.
Reminder:
The decibel is a logarithmic unit of measurement that expresses the magnitude of a physical quantity relative to the reference quantity of the same unit.
It is a dimensionless quantity.
The amplitude in decibel mode is calculated by the following formula: ![]() ,
,
where
- An is the measured amplitude corresponding to the harmonic n,
- A0 is the reference amplitude, corresponding to 0 dB
In order to operate in decibel mode, there are two possibilities in Flux to set the reference value:
- either to define the value of the amplitude in decibel for the first harmonic, that
is the component
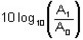 (
(  is set by default at 100),
is set by default at 100), - or to define the reference value A0 for 0 dB ( A0 is set by default at 1).
Displaying or not the DC component
This option displays the spectrum component corresponding to the 0 order harmonic.
Perform the spectrum analysis
To perform the spectrum analysis, i.e. plot the extrapolated curve of a 2D curve (function of spatial quantities or input/output parameters) and display the corresponding spectrum, follow instructions below:
| Step | Action |
|---|---|
| 1 |
In the menu , click on Spectrum analysis (FFT) |
| 2 |
In the selection dialog, choose the 2D curve entity |
| 3 |
In the Spectrum analysis (FFT) dialog:
|
| → |
|