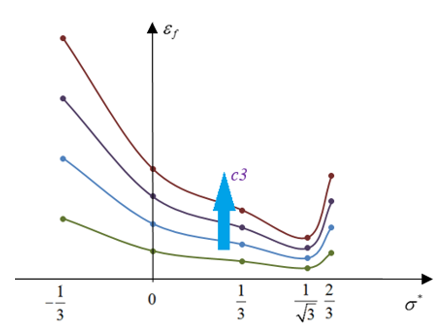
Radiossでは、/FAIL/BIQUADが延性材料用で最もユーザーフレンドリーな破壊モデルです。この破壊モデルは、ひずみベースの簡易化された非線形破壊基準を線形損傷累積と共に使用します。
破壊ひずみは、5つまでのユーザー入力破壊ひずみから曲線のフィッティングを用いて計算された2つの放物線関数によって記述されます。
デフォルトでは、
/FAIL/BIQUAD(
S-Flag=
1)は2つの放物曲線を用いて塑性破壊ひずみ
を応力軸性
の関数として表現します。2つの放物曲線は下記を使用します:
(1)
(2)
ここで、
-
、
、
、
、
、
- 放物線係数
-
- 応力軸性
-
および
- 塑性破壊ひずみ
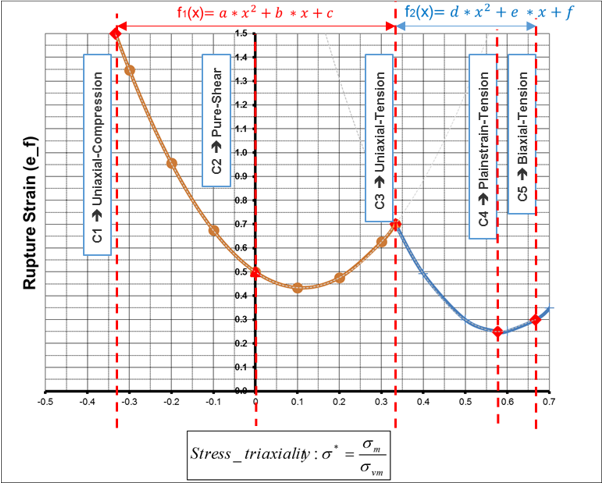
図 1. 2つの放物線から成る/FAIL/BIQUAD破壊ひずみ曲線
放物線係数
、
、
、
、
、
は、塑性破壊ひずみ
c1-
c5入力値に基づいた曲線フィッティングを用いて
Radiossによって計算されます。計算された放物線破壊ひずみ曲線は負の破壊ひずみ値を有します。これらの負の値は1E-6の破壊ひずみによって置き換えられ、これは、非常に大きな損傷累積と脆性の挙動をもたらします。曲線フィッティングの結果は、Starter
*0000.outファイルにあります。
Bi-Quadratic FAILURE
--------------------
c1. . . . . . . . . . . . . . . . . . .= 0.2419E+00
c2. . . . . . . . . . . . . . . . . . .= 0.1900E+00
c3. . . . . . . . . . . . . . . . . . .= 0.1585E+00
c4. . . . . . . . . . . . . . . . . . .= 0.1437E+00
c5. . . . . . . . . . . . . . . . . . .= 0.1394E+00
COEFFICIENTS OF FIRST PARABOLA
-----------------------------
a . . . . . . . . . . . . . . . . . . .= 0.9180E-01
b . . . . . . . . . . . . . . . . . . .= -0.1251E+00
c . . . . . . . . . . . . . . . . . . .= 0.1900E+00
COEFFICIENTS OF SECOND PARABOLA
-----------------------------
d . . . . . . . . . . . . . . . . . . .= 0.3753E-01
e . . . . . . . . . . . . . . . . . . .= -0.9483E-01
f . . . . . . . . . . . . . . . . . . .= 0.1859E+00
c1–
c5塑性破壊ひずみ定義は:
- c1
- 単軸圧縮の塑性破壊ひずみ
- c2
- せん断の塑性破壊ひずみ
- c3
- 単軸引張の塑性破壊ひずみ
- c4
- 平面ひずみ引張の塑性破壊ひずみ
- c5
- 2軸引張の塑性破壊ひずみ
M-Flag入力オプション
M-Flag入力オプションに応じて、
c1-
c5値の定義には3つの異なる方法があります。
デフォルトの挙動
デフォルトでは、
c1から
c5には、0以外の値を入力する必要があります。しかしながら、破壊情報が欠落している場合、独特なデフォルト値が存在します。
- 材料破壊の挙動が未知である場合、c1からc5までは0.0に設定され、軟鋼挙動(M-Flag=1)が使用されます。
- 引張破壊値のみが既知である場合、c3が定義されます(
)。軽度な鋼鉄挙動が使用され、ユーザー定義のc3値によってスケーリングされます。
- 材料挙動が既知である場合、M-Flagが定義され、c3は期待される引張破壊に従った破壊モデルの調整に使用できます。選択された材料挙動は、ユーザー定義のc3値によってスケーリングされます。
- それ以外の場合、c1~c5は定義される傾向にあり、デフォルト値0.0が使用されます。
要素破壊処理
損傷累積法は、要素内の各積分点において発生した塑性ひずみの量を以下を用いて合計するために使用されます:
(3)
ここで、
-
- 損傷
-
- 積分点の塑性ひずみの変化
-
- 現在の応力軸性における塑性破壊ひずみ
シェル要素については、積分点が
に達すると、積分点応力テンソルがゼロにセットされます。厚み全体の破断した積分点の比率がP_thickfailに等しくなると、要素が破断し、削除されます。ソリッド要素では、積分点が
に達すると、要素は削除されます。
平面ひずみは大域的最小
S-Flag=2オプションは、塑性ひずみ曲線の大域的最小が平面ひずみ応力軸性位置c4で起こるようにするために使用できます。これは、2つ目の式を2つの別々の2次サブ関数に分割することで達成されます。
材料の不安定性のモデル化(肉やせ)
シートメタルのような材料では、材料の厚みの減少や拡散ネッキングが引張載荷中に現れることがあります。これは
肉やせと呼ばれ、通常
の応力軸性範囲で起こります。

図 4.
/FAIL/BIQUADでは、この肉やせをオプション
S-Flag=
3および
Inst_startを使ってシミュレートすることが可能です。このオプションは、
S-Flag=
2と同じ塑性破壊ひずみオプションを使用し、応力軸性
および
の間の肉やせの開始を表す曲線を定義する2つの追加の2次関数を追加します。この曲線の最小値は、
Inst_startフィールド内でユーザーによって定義され、平面ひずみ引張
で生じます。この肉やせ曲線を用いて、2番目の肉やせ損傷値が計算され、肉やせによる破断はすべての積分点が
に達した際にのみ起こります。肉やせ基準は、Marciniak-Kuczynski解析に基づきます。
1

図 5. デフォルトの破壊ひずみ曲線. 追加の肉やせ曲線(青色)
S-Flag=1または2の使用時、損傷累積は、塑性曲線(図 6で赤色)で塑性ひずみに達した際に始まります。
S-Flag=3が肉やせの描写に使用される場合、損傷累積は、肉やせ曲線(
図 6で青色)で塑性ひずみに達した際に始まります。肉やせについて、すべての積分点が損傷に至ると(
)要素は削除されます。肉やせのせいではない要素の削除は
P_thickfailで定義されます。
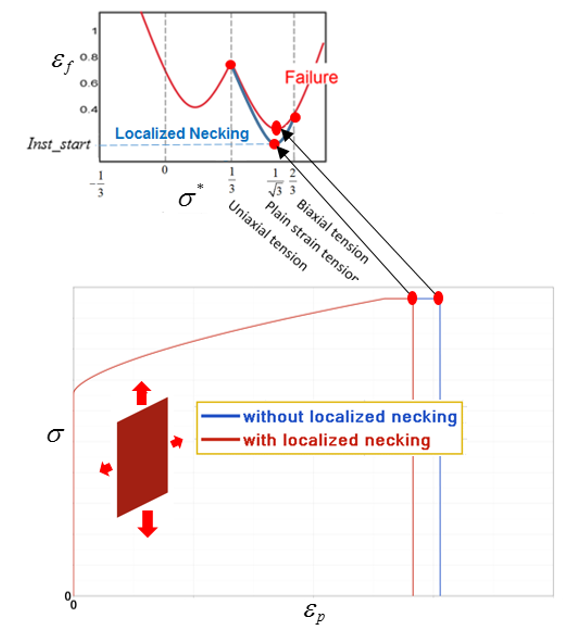
図 6.
破壊限界の摂動
材料の不完全性または製造プロセスのせいで、材料の破壊ひずみは場所によっては全く同じではない場合があります。したがって、破壊限界の非常に小さい摂動は存在し得ます。
M-Flag>0を
/PERTURB/FAIL/BIQUADと使用する際は、破壊限界の統計的分布が、破壊モデルに割り当てられている各要素に適用されます。これは、
/FAIL/BIQUAD、
c3に適用されている破壊のスケールファクターのランダム分布または正規分布を計算することによって行われます。2つの異なる分布の手法が
図 7と
図 8に示されています。

図 7. ランダム分布. Idistri=1、Starter *0.outファイル内の破壊限界

図 8. 正規(ガウス)分布. Idistri=2、Starter *0.outファイル内の破壊限界
/FAIL/BQUADは、右記の値に依存するユーザー定義の速度
r1、
r2、
r4および
r5または事前定義された材料のひずみ速度値を用いて破壊曲線全体をスケーリングするために
/PERTURB/FAIL/BIQUADによって生成される
c3の非常に小さな摂動を使用します;
M-Flag.
c3
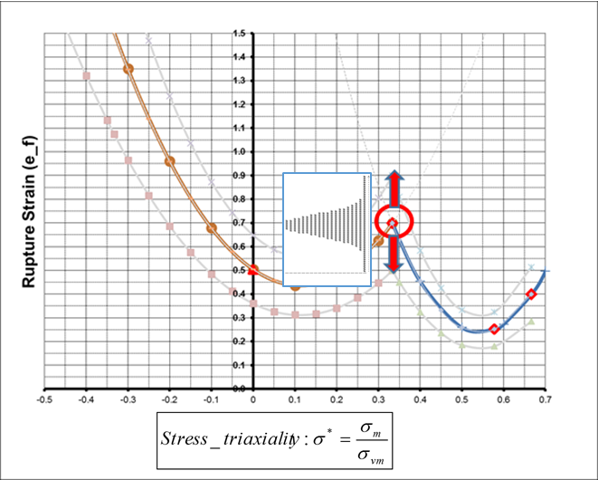
図 9.
1 Pack, Keunhwan, and Dirk Mohr."Combined necking & fracture model to predict ductile failure with shell finite elements."
Engineering Fracture Mechanics 182 (2017):32-51