モデル化のツール
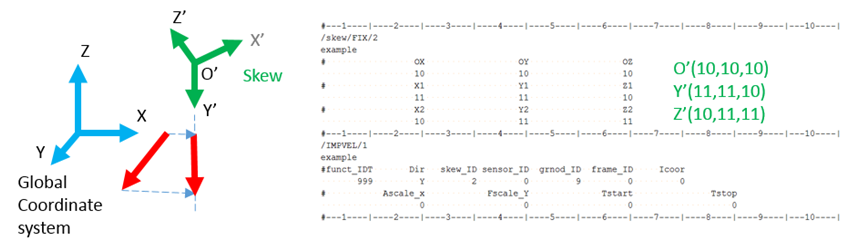
スキューとフレーム(/SKEW & /FRAME)
スキューとフレームは局所座標の定義に用いられます。
- 境界条件
- 集中荷重
- 強制速度
- 剛結の向き
- 剛体に付加される慣性フレーム
- 一般スプリング参照フレーム
- ビームタイプスプリング初期参照フレーム
- 節点時刻歴出力フレーム
- スキュー参照
- これは全体座標系に関して局所座標系の諸量を定義する投影参照です。実際、スキューの原点は、移動スキューが定義された場合でもその移動の間最初の位置に留まります。この場合では、運動学的な諸量の計算の参照で、単純な投影マトリックスが用いられます。
- フレーム参照
- これは移動または固定参照です。諸量は移動する参照フレームまたは参照フレームの種類に依存しないその原点に関して計算されます。移動参照フレームでは、その参照の位置と向きは、移動の間、時間で変化します。節点位置で定義されたそのフレームの原点は節点に結びつけられています。
断面(/SECT)
断面を使用して、一群の要素と節点を通過する力、モーメント、エネルギーを測定します。断面の変位をファイルに保存しておき、より小型の断面モデルに適用する変位として使用できます。
- 節点のグループと要素のグループ。節点と要素は/SECTでユーザーが選択できます。frame_ID、/SECT/PARAL、または/SECT/CIRCLEで/SECTを使用して切断面を定義することにより、節点と要素を自動的に選択することもできます。
- 3つの節点を選択することで定義した局所出力座標系
- 力とモーメントを計算するための参照点
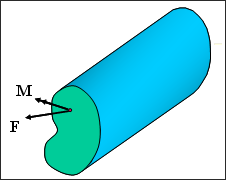
図 3. 向きのあるソリッドのための断面定義
切断面
/SECTでは、切断面は無限大の大きさを持ち、要素のグループと節点のグループの単位で定義します。これらの要素と節点はユーザー定義であり、可能であれば1列に配置します。
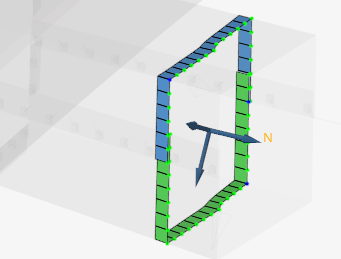
図 4. 手動で選択した要素と節点
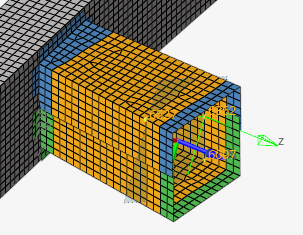
図 5. 局所座標系を使用して定義した切断面に対して定義した要素グループ(オレンジ色)
NUMBER OF NODES. . . . . . . . . . 40
NODES:
6062 6064 6055 6074 6076 5895 6078 6173 6166 6136
6174 6181 6182 6219 6210 6220 6227 6228 6359 6358
...
NUMBER OF SHELL ELEMENTS . . . . . 43
SHELL N1 N2 N3 N4
5819 0 1 1 0
5820 0 1 1 0
5826 0 0 1 0
5839 0 1 1 0
...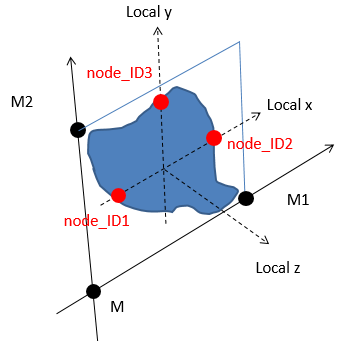
図 6. /SECT/PARALの定義
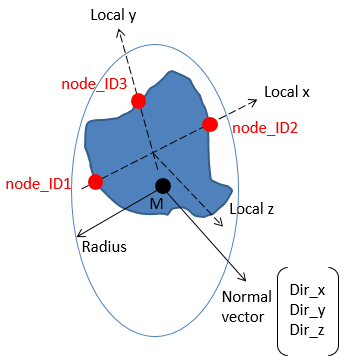
図 7. /SECT/CIRCLEの定義
どのタイプの断面でも、ソリッド、シェル、トラス、ビーム、スプリングの各要素を切断できます。接触インターフェースも選択できます。
frame_ID、/SECT/PARAL、または/SECT/CIRCLEで/SECTを使用している場合、断面の計算に使用される節点は、選択した要素の+z側に存在します。これらの節点は自動的に定義されるので、要素グループをパート単位で定義できます。したがって、各パートを再メッシュしていれば要素グループを再定義する必要はありません。
切断面の局所座標系
断面の力とモーメントを計算するには局所座標系を定義する必要があります。
- 節点のnode_ID1とnode_ID2は断面の局所X軸を定義します。
- 節点のnode_ID1、node_ID2、node_ID3は断面の局所xy平面を定義します。
- 局所座標系のy軸は、node_ID3を局所座標系のx軸に対して直角に投影することによって定義します。
- これにより、局所座標系のx軸とy軸の交点が、その局所座標系の原点になります。
- xy平面に直交する断面法線が局所座標系のz軸になります。
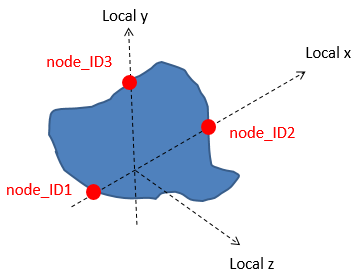
図 8. 節点を使用して定義した、断面の局所座標系
HyperMeshで/SECTを作成すると、この3節点が自動的に選択されます。この3節点を手動で選択する場合は、断面の計算に使用する節点のグループに属する節点を選択することをお勧めします。これにより、断面の変形に伴って移動する局所座標系とすることができます。
また、/SECTを使用していて3節点を定義せず、frame_IDを定義している場合は、/FRAME/MOVのxy平面が局所座標系として使用されます。/FRAME/MOVを定義している場合は、断面の計算に使用する節点のグループに属する節点を使用することをお勧めします。
力とモーメントの計算
断面力は、選択した要素にかかる節点力の合計です。
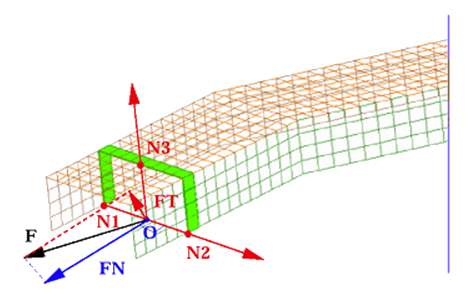
図 9. 断面での法線方向断面力と接線方向断面力
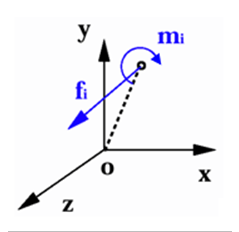
図 10. 節点の合力とモーメント
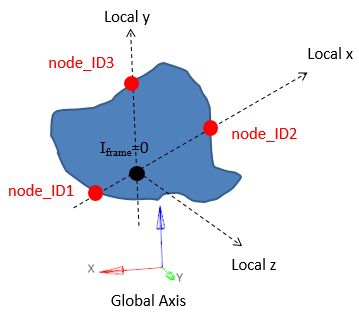
図 11. Iframe=0: 断面出力に使用する局所座標系と原点
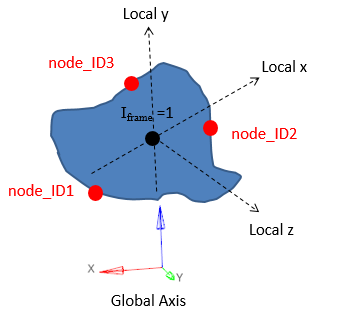
図 12. Iframe=1: 断面の幾何学的中心を原点とする局所座標系
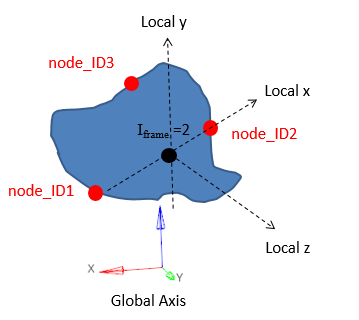
図 13. Iframe=2: 断面の重心を原点とする局所座標系
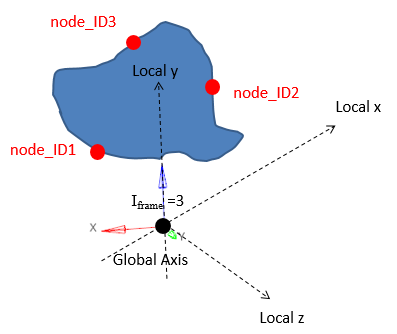
図 14. Iframe=3: 中心を全体座標系の原点とする局所座標系
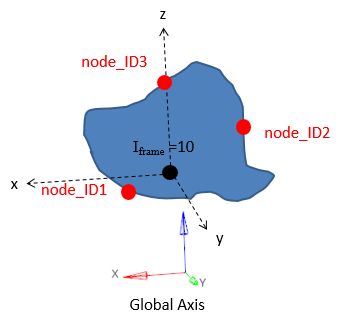
図 15. Iframe=10: 局所座標系の原点を中心とする全体座標系
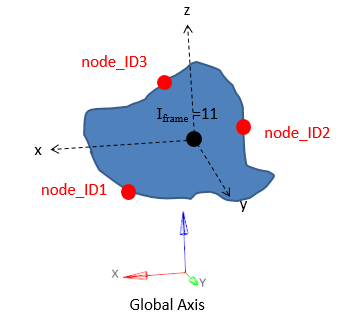
図 16. Iframe=11: 断面の幾何学的中心を原点とする全体座標系
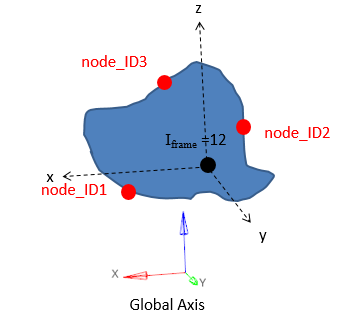
図 17. Iframe=12: 断面の重心を原点とする全体座標系
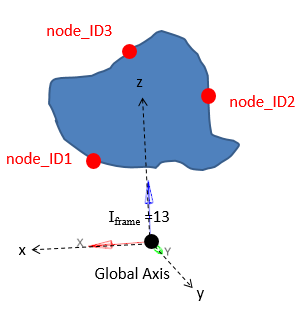
図 18. Iframe=13: 中心を全体座標系の原点とする全体座標系
断面の出力
2種類の断面出力を使用できます。
そのひとつは、断面に作用する力とモーメントの合計で構成する時間暦出力/TH/SECTIOです。この出力は、広く使用されている出力を変数グループGLOBAL、LOCAL、およびCENTERとして、全体座標系と局所座標系のどちらでも記述できます。
もうひとつは、断面で各節点が示す変位、および必要に応じて力とモーメントを、SC01ファイルに書き込んだ断面出力です。このファイルを、適用する変位として別の切断面モデルに読み取ります。 RD-E:5400 カット手法 は、使用できる切断面手法の一例です。この例では、ISAVE=1または2を指定してフルモデルを実行し、変位および必要に応じて合成断面力とモーメントをファイルfile_nameSC01に保存します。
つづいて、ISAVE=100または101を使用して定義した断面で別のカットモデル(サブモデル)を作成し、断面ファイルの節点の変位を読み取ります。node_ID1、node_ID2、およびnode_ID3の3節点またはframe_IDによって断面に定義した局所座標系は、データの保存(ISAVE=1または2)およびデータの読み取り(ISAVE=100または101)で使用した座標系と同じであることが必要です。
フルモデルでISAVE=2を使用し、カットモデルでISAVE=101を使用している場合、フルモデルとカットモデルとの間で、断面(/TH/SECTIO)での合成断面力とモーメントに見られる差異がRadiossによって出力されます。
カットモデル手法が不要であれば、解に要する時間を短縮し、メモリ消費量を削減するために、ISAVE =0の設定をお勧めします。
フィルター
- フィルター処理対象の変位
- 指数移動平均フィルター処理の定数
- フィルター処理前の現在の変位
- 前の時間ステップにおける変位
推奨の処理は次のとおりです。
: -3dBフィルター処理
: -6dBフィルター処理
- フィルター処理周期
- モデルの時間ステップ
-3dBフィルターの場合は、多くの場合、フィルター処理周期、を使用します。