異なる材料試験では、結果として得られる材料の力学的特性が異なる場合があります。
一般的な金属の材料試験は引張り試験です。この試験の応力-ひずみ曲線では、材料の降伏点、ネッキングポイント、および破壊点を確認することができます。
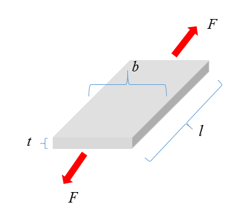
図 1. 力(F)および長さ(l)が測定される
工学応力-ひずみ曲線は、以下によって生成できます:
(1)
(2)
ここで、
-
- 初期状態における断面積
-
- 初期長さ
力-伸び曲線または工学応力-ひずみ曲線では、3つのポイントが重要です。
- 降伏点: 材料が降伏し始めるポイント。降伏前の材料は弾性状態(ヤング率Eを測定できる)、降伏後は不可逆的な塑性ひずみの状態にあるとみなすことができます。
- この試験の一部の材料は、まず上降伏点(ReH)に達してから、下降伏点(ReL)まで下がります。工学応力-ひずみ曲線では、下降伏応力(保守的値)を取得できます。
- 材料によっては、降伏点を容易に見つけることができない場合もあります。降伏応力として塑性ひずみの0.1または0.2%の応力を指定します。
- ネッキングポイント: 材料が工学応力-ひずみ曲線の最大応力に達したポイント。このポイントを過ぎると、材料は軟化し始めます。
- 破壊点: 材料が破壊されるポイント。
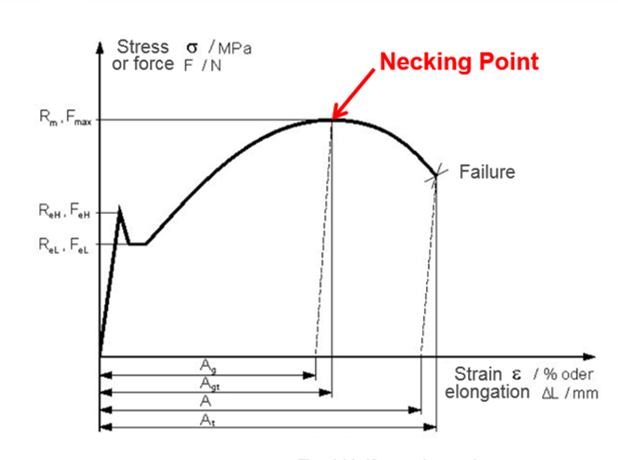
図 2.
- Rm
- 最大抵抗
- Fmax
- 最大力
- ReH
- 上降伏レベル
- ReL
- 下降伏レベル
- Ag
- 均一の伸び
- Agt
- 均一の伸びの合計
- At
- 全破壊ひずみ
Radiossのほとんどの材料で要求される真の応力-ひずみ曲線。ただし、工学応力-ひずみと真応力-ひずみの両方で材料データを入力できるLAW2は除きます。
図 3で、工学応力-ひずみ曲線(青色)は以下を使用して求めます:
(3)
(4)
この結果は真応力-ひずみ曲線(赤色)になります。緑色で示されている塑性真応力-ひずみ曲線は、塑性ひずみが0から始まります。
LAW36、
LAW60、
LAW63などで必要とされるのは、この緑色の塑性真応力-ひずみ曲線です。
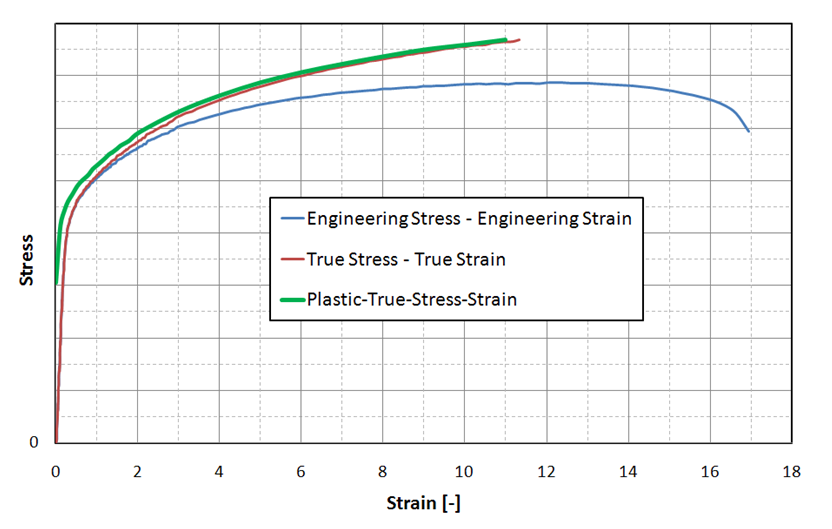
図 3.
真応力-ひずみ曲線は、材料のネッキングポイントまで有効です。ネッキングポイント以降は、硬化について、材料曲線を手動で定義する必要があります。別の材料則を使用することで、
Radiossでは真応力-ひずみ曲線を100%外挿することができます。
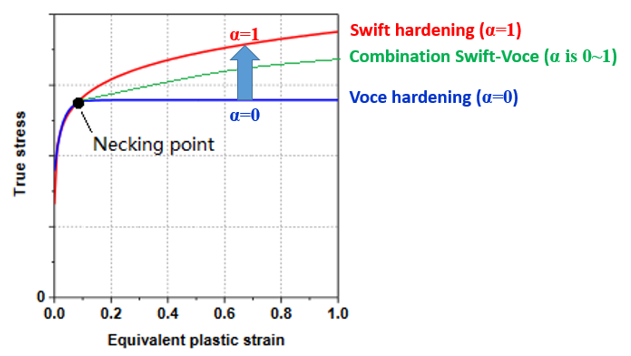
図 4.



