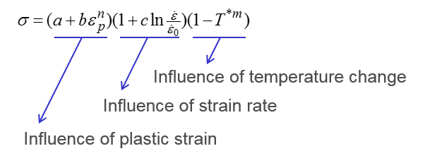
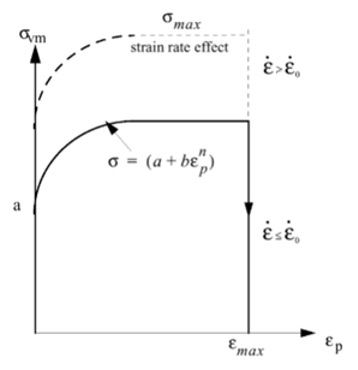
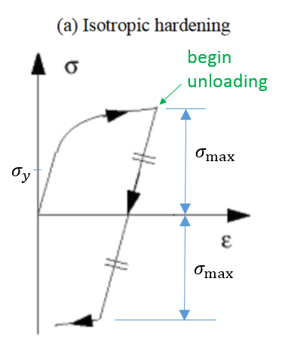
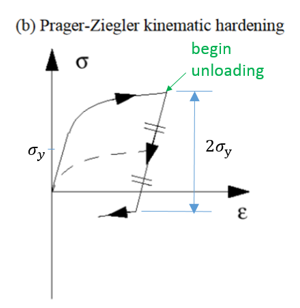
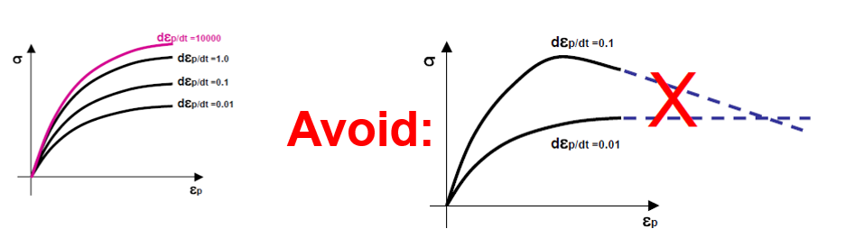
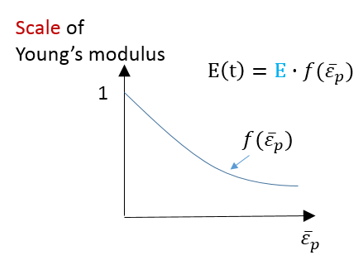
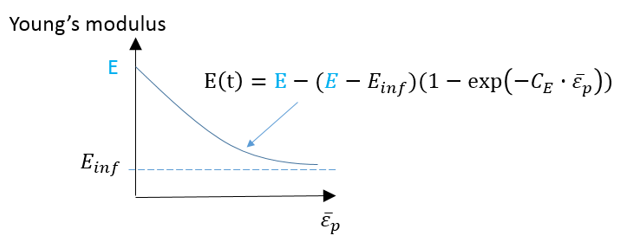
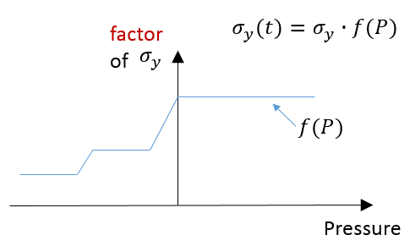
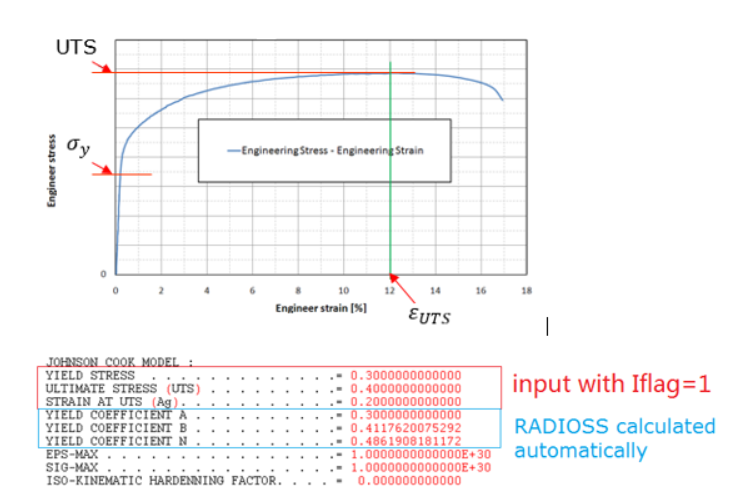
Radiossでは、LAW32、LAW43、LAW72、LAW73、LAW74、LAW78、およびLAW93の各材料則でHILL基準を使用します。
ひずみ速度
ランクフォードパラメータ
は、面内の塑性ひずみと厚み方向の塑性ひずみ
との比率です。
(9)
ここで、は、直交異方性方向1に対して成す角度です。
は、直交異方性方向1に対してさまざまな角度で切断した多くの試料で測定できます。荷重の方向を直交異方性の方向1とした引張試験で測定したと同様。 荷重の方向が直交異方性の方向1と直交する引張試験で測定した
ひずみ速度は、試料の厚み方向のひずみに対する試料の幅方向のひずみの比率です。
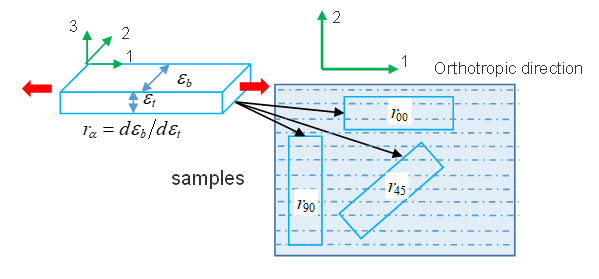
図 10.
この場合のHILLパラメータは次のようになります:
(10)
(11)
(12)
(13)
ここで、。
LAW32、LAW43、およびLAW73のHILL基準は次のとおりです:
(14)
|
|
|
|
|
|
これらのすべての基準でランクフォードパラメータ(ひずみ速度)が要求され、HILLパラメータがRadiossによって自動的に計算されます。
降伏応力比
LAW93で使用する降伏応力比は次のとおりです:
(15)
降伏応力比
を取得するには、2つの荷重ケースの降伏応力を測定する必要があります。
- 引張試験で得られた降伏応力
- せん断試験で得られた降伏せん断応力
LAW93でパラメータ入力を使用する場合は、初期応力パラメータを参照降伏応力として取得します。曲線入力を使用する場合は、曲線から読み取った降伏応力を参照降伏応力として取得します。
シェルの4つのHILLパラメータは
Radiossによって自動的に計算されます。
(16)
(17)
(18)
(19)
LAW74では、降伏応力比
が、降伏応力
と
入力で直接使用され、ソリッドの6つのHILLパラメータが
Radiossによって自動的に計算されます。
|
|
|
|
|
|
シェル要素の場合は、とを取得します。