Radiossの座標系
- 全体座標系(、および)
- 固有座標系(アイソパラメトリックフレーム)()
- 局所要素座標系(、および)
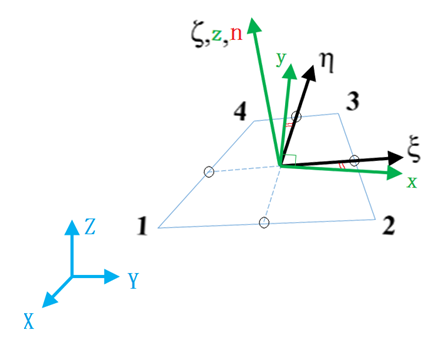
図 1. 4節点シェル要素
(、および)- 全体デカルト固定座標系:
() - 固有座標系(非正規化座標系)
- は、ライン14の中点からライン23の中点に向かいます。
- は、ライン12の中点からライン34の中点に向かいます。
- 平面()はシェル要素の中立面内にあり、は中立面に垂直です。
- は中立面に垂直です。
- (および)は中立面内にあります。
- とは、右記の間が同じ角度になるように配置されます; と、と
()と(、および)の原点は同じで、中点を結んだ線の交点になります。
3節点シェル要素
(、および)- 全体デカルト固定座標系:
() - 固有座標系(非正規化座標系)
- は節点1から節点2に向かいます。
- は節点1から節点3に向かいます。
- 平面()はシェル要素の中立面内にあり、は中立面に垂直です。
- は中立面に垂直です。
- は節点1から節点2に向かいます。
- はに直交し、(および)は中立面内にあります。
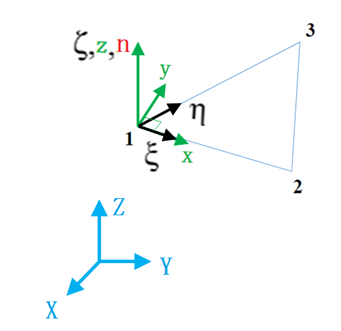
図 2.
ソリッドおよび厚肉シェル(ヘキサ)
- 全体座標系(、および)
- 固有座標系(、および)
- 局所要素座標系(、および)
- 材料座標系
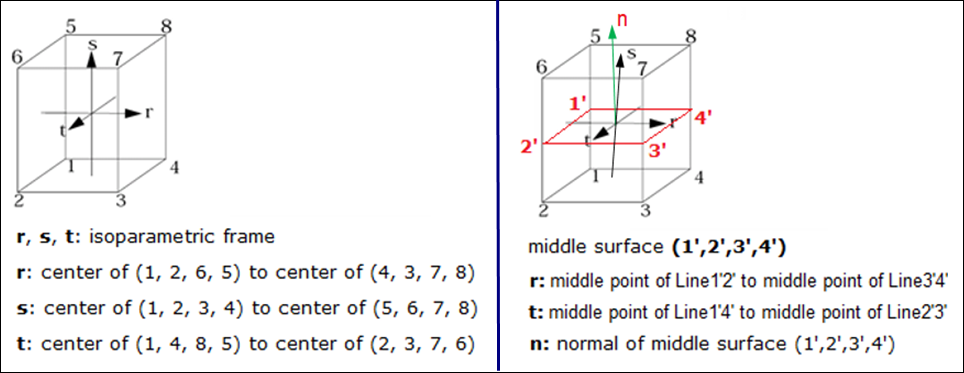
図 3. ソリッドおよび厚肉シェル(ヘキサ)
(、および)- 全体デカルト固定座標系:
- は、サーフェス(1、2、6、5)の中心からサーフェス(4、3、7、8)の中心に向かいます。
- は、サーフェス(1、2、3、4)の中心からサーフェス(5、6、7、8)の中心に向かいます。
- は、サーフェス(1、4、8、5)の中心からサーフェス(2、3、7、6)の中心に向かいます。
- も、線1’と2’の中点から線3’と4’の中点に向かいます。
- も、線1’と2’の中点から線3’と4’の中点に向かいます。
- は中立面(1’、2’、3’、4’)に垂直です。
(, 、および) - 局所座標系(直交、非正規化要素座標系):
中立面(1’、2’、3’、4’)内の局所座標系は、シェル要素の中立面 (1、2、3、4)と同じです。ソリッド内のはシェル要素内のと同じです。
テトラ要素
- は節点4から節点1に向かいます。
- は節点4から節点2に向かいます。
- は節点4から節点3に向かいます。
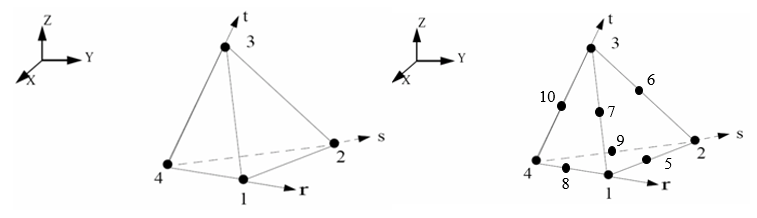
図 4. テトラ要素
材料座標系
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| VX | VY | VZ | |||||||
ベクトルと角を使用して、材料方向1()を定義できます(法線nに沿ってベクトルを中立面に投影するとベクトルを取得できます。ベクトルを角だけ回転させると、材料方向を取得できます。材料方向は通常、繊維方向です。複合材の場合は、1つのベクトルと別のにより、別のプライを定義することができます。
- はシェルの中立面に垂直です。
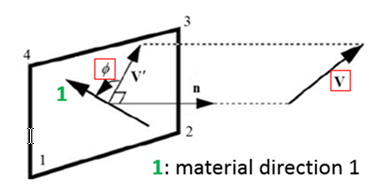
図 5.
- Iorth=0(デフォルト): 直交異方性方向は局所共回転基準に従います。との間の角はシミュレーションの間一定です。局所フレームで内力が計算され、全体座標系に回転されます。この定式化は、大きな回転が発生すると、より正確になります。
- Iorth=1:直交異方性方向は局所アイソパラメトリックフレームに付加されます。との間の角は、シミュレーション中に更新されます。これは、ベクトルのとへの投影がシミュレーションの間、常に一定となるように更新されます。純せん断はこの方法ではよく表されませんが、引張りは良好に表現されます。したがって、この方法は通常、エアバッグの繊維方向を定義するために使用されます。
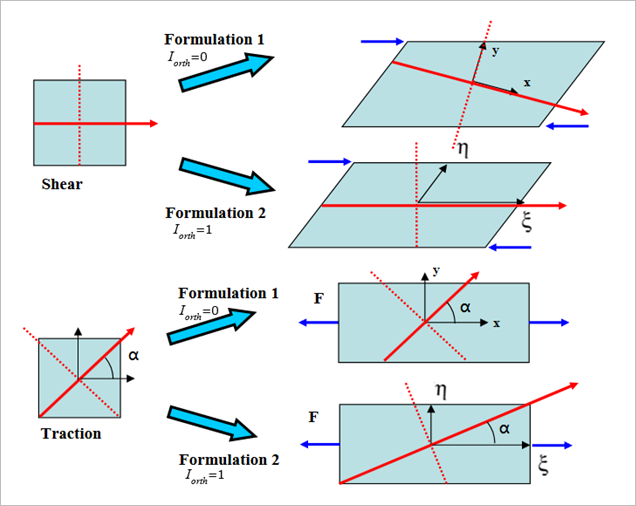
図 6.
- IP=0
- Skew_IDを使用
- IP=1
- 平面(,) + a角
- IP=2
- 平面(,) + a角
- IP=3
- 平面(,) + a角
- IP=11
- 平面(,) + 参照ベクトルの平面(,)上の直交投影
- IP=12
- 平面(,) + 参照ベクトルの平面(,)上の直交投影
- IP=13
- 平面(,) + 参照ベクトルの平面(,)上の直交投影
- 任意のIsolidとIframeパラメータで、定義は同じです。
- 最も単純なケースでは、直接スキュー(IP=0)を使用した材料方向、、およびが推奨されます。
- IP > 0の場合は、アイソパラメトリック非直交座標系、、およびを使用して材料方向を決定します。
- 最初の材料軸は、IPに従って決定されます。
- 例えば、IP=1の場合
- 最初の材料軸およびは直交し、(および)面で角だけ回転されます。
- 3つ目の材料軸は、および面に垂直です(とのベクトル積)。
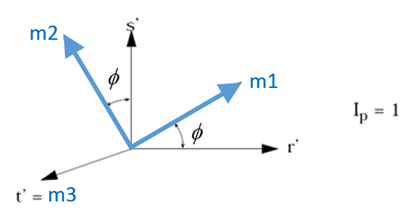
図 7. - (、および)座標系は直交座標系で、非直交アイソパラメトリック座標系(、および)から生成されます。
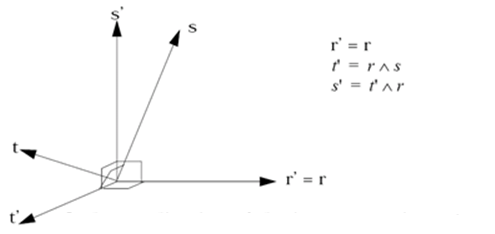
図 8. アイソパラメトリック座標系の直交化
IsolidおよびIframeパラメータに応じて、/PROP/TYPE6 (SOl_ORTH)を使用してRadiossでヘキサ要素(8節点3次元ソリッド)に対して3つの座標系定義が使用されます。
全体座標系定義
- 定義1: ソリッド、Isolid=1, 2, 17 + Iframe=0, 1(デフォルト)
全体座標系が使用され、要素座標系(非共回転定式化)は使用できません。
要素座標系定義
- 定義2:ソリッド、Isolid=1, 2, 17 + Iframe=2
要素座標系(Iframe=2 共回転定式化)が使用されます。
- 定義3:ソリッド、Isolid=14または24
Iframeパラメータによる影響はありません。要素座標系が使用され、共回転定式化はすでに定義されています。