普通、微小ひずみ定式化は変形が小さい問題のシミュレーションに用いられます。典型的な適用分野は、線形弾性での検討です。弾塑性挙動と大変形での非線形問題では、大ひずみと大変位定式化を用いることが推奨されます。
大きなメッシュのゆがみを伴ういくつかの問題では、大ひずみ定式はいくつかの制限が生じます。時間ステップの減少が大きくなり過ぎると、CPU時間が大きく増加し、ソリッド要素が負の体積に到達すると、計算がストップするか、その要素が削除されなければならなくなります。
微小ひずみ定式化ではこれらの制限はなくなります。大変形の場合に微小ひずみの定式を用いることは驚くべきことかも知れませんが、要素削除よりは良い解になり得ます。ある材料、例えばハニカムのようにポアソン効果のない場合、適当な応力-ひずみ曲線を用いるだけで微小ひずみの制限は修正できます。
大ひずみ定式化
デフォルトでは、Radiossは大ひずみ、大変位定式化を陽的時間積分と共に用います。それぞれのサイクルで、形状関数の微分を計算することにより、大変位定式化が得られます。ひずみ増分の計算より大ひずみの定式化の結果となります。そのため、応力とひずみは、真応力と真ひずみとなります。
Cauchy応力(真応力)の時間積分は次のように実行されます:
(1)
応力速度の客観性は応力テンソルが材料の剛体回転に従うことを意味します。応力速度は要素の平均剛体回転とひずみ速度の関数となります。陽解法スキームの安定性は Courantの安定条件により与えられます:
(2)
ここで
は要素の特性長さ、
は音速です。時間ステップはそれぞれのサイクルで計算されます。大きな要素変形では大きな時間ステップの減少を起こし得ます。非常に大きな変形では、負の体積に到達することがあり、その時には体積の応力積分が不可能になります。
微小ひずみ定式化
時間の間での一定のヤコビアンマトリックスと一定体積を仮定すると、前の式は微小ひずみ定式化に退化します。全ての特別な値は、時刻 t=0(または微小ひずみが定式化が開始された時)で定義された値になります。
時間ステップは一定になります:
(3)
このため、負の体積は計算に影響を与えなくなります(初期の体積のみが用いられるため)。しかし、ハニカムなどのある特定の材料挙動に微小ひずみの仮定を受け入れることが可能でも、微小変位の仮定は衝突解析には明らかに推奨されません。
応力の客観性では、ヤコビアンマトリックスの時間変換は要素の変形と要素の剛体回転に依存します。剛体並進移動はヤコビアンマトリックスに影響を与えません。要素の変形が考慮されない場合、微小ひずみの定式化が得られます。要素の剛体回転が無視できる場合、微小変位の定式化が得られます。
に到達した後で微小ひずみ定式化に切り替えるために、Engineファイルで以下のオプションを用いることができます:
/DT/BRICK/CST
/DT/SHELL/CST
/DT/SH_3N/CST
注: 一部のソリッド材料則では、音速は圧力依存です。それゆえ、その時間ステップは
よりも若干小さくなる可能性があります。
応力とひずみの更新(/PROP)
Radiossでは2つの定式化が利用可能です(
図 1):
- 共回転定式化(CR): それぞれの要素の有限要素方程式は2つの座標系を参照します。要素の剛体移動を計算するために固定または基礎の形状が用いられます。次に変形した現在の状態は、初期参照の剛体移動によって得られた共回転形状を参照します。
- 更新ラグランジ定式化(ULF): 参照は最後の既知の(受け入れられた)解となります。これはステップの間固定されたままで、それぞれのステップの終了時に更新されます。
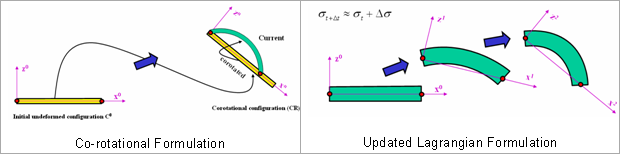
図 1. Radiossでの更新手法
共回転定式化は、幾何学的非線形構造解析の最も最近の定式化です。これは微小ひずみの材料非線形性を幾何学的非線形性から分離し、材料非線形性による異方性挙動のフレームからの中立性の問題を自然に取り扱うことができます。以前からある
Radiossソリッド要素では、共回転定式化はオプションで、計算前にアクティブにする必要があります(RADIOSS Starter入力マニュアルの
/PROP/SOLID参照)。
注: 更新ラグランジ定式化では、それぞれのサイクルでの更新の誤差の累積のため、大きなせん断変形を受けるソリッドの結果を正しく取り扱えないことがあり得ます。特に、大きなせん断変形や、大きな剛体移動を受ける要素では、共回転定式化の使用を強く推奨します。
