シェル要素

これらは膜、曲げ、およびせん断を含んでおり、板厚方向の直応力は常に0です。

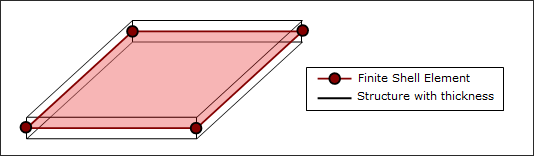
図 1. シェル要素

Radiossでは、標準のシェル要素は横せん断変形のあるMindlin板要素です。これらの要素は、横せん断による変形を考慮せず、中立面に直交する平面が変形の間も直交を保つ標準のKirchhoff要素よりも精度は高くなります。

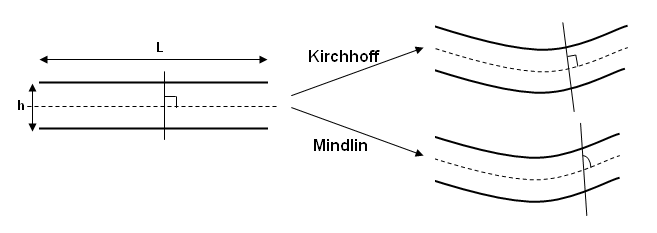
図 2. シェルモデル

Kirchhoffモデルは精度的に劣っていても、L/hの比が20より大きい場合、このKirchhoffによる条件は正確です。しかしL/hの比が10と20の間の場合、中立面に直交する平面が変形の間も直交するという仮定条件は成り立たず、横せん断ひずみを考慮したMindlin板要素の使用を考えるべきです。Radiossでは、低減積分シェル要素（4節点および3節点シェルの両方）は Mindlinの仮定に基づいています。要素の中立面を節点からオフセット可能にする特定の定式化はないため、薄肉構造を中立面上で離散化 することは非常に重要です。

シェル要素の定式化は衝突解析では非常に重要な役割を持ちます。Radiossのシェル要素は主にMindlin-Reissnerシェル理論に基づいています。この定式化はやや厚いシェルと薄いシェルに対して有効です。低減積分要素が、そのコストの低さから最もよく使われています。

表 1. シェル要素ライブラリ

メッシュ	要素名	積分点の数	アワグラス定式化	コメント
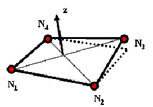	BT （古典的なQ4）	1	ペナルティ法に基づいた4タイプ	一定法線ベクトル アワグラス定式化タイプ 3と4 がデフォルトで用いられるタイプ1よりもずっと優れる
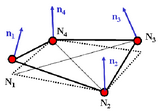	QEPH	1	物理安定化	節点での法線ベクトル 出力にアワグラスエネルギーなし
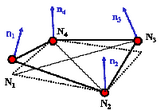	QBAT	2x2	完全積分要素	節点での法線ベクトル アワグラスエネルギーなし
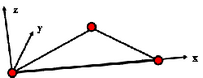	C0	1	---	平面要素 アワグラスエネルギーなし
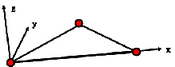	DKT18	3	---	Kirchhoff シェル（薄肉シェルのみ） 高い t/Lでは低い時間ステップ
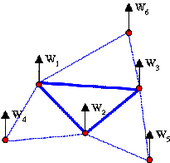	S3N6	1	---	Kirchhoff シェル（薄肉シェルのみ） 回転自由度なし 側面の回転は隣接要素の鉛直変位によりきめられる

結果の品質とメッシュの関係を図的に図 3に示します。

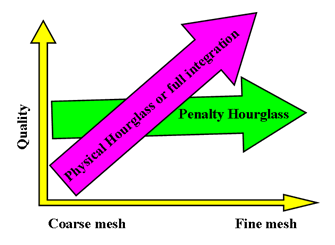
図 3. 異なるメッシュに対するシェル定式化の利用

板厚方向の積分

弾性シェルでは、板厚方向の直応力の変化は線形になります、このため、内部エネルギーは解析的な積分で得ることができます。塑性の場合は、応力分布が非線形となり、その非線形性を考慮するためには少なくとも３積分点が必要になります。応力の非線形分布はいくつかの付加された積分点で値を測定することにより近づくことができます。内部エネルギー推定の品質は積分点の数と コストに依存します。コストと品質の良い妥協点は、材料の非線形性と板厚と曲げの比を考慮するとにより見つけることができます。積分点の数は、Radioss V5xで10点まで増加されました。特に板厚が2mm以上の場合、5積分点の使用はより良い結果をもたらしますが、CPU時間の増加は無視できなくなります。曲げと横せん断のない膜要素のモデル化には１積分点のみの使用で十分です。弾性材料（LAW1）では、解析的計算によりこのオプションは無視されます。

弾性材料の膜要素を得る1つの方法は弾塑性材料則（Johnson-Cook則）を非常に高い降伏応力（例えば： 1e+30）で用いることです。1e+30

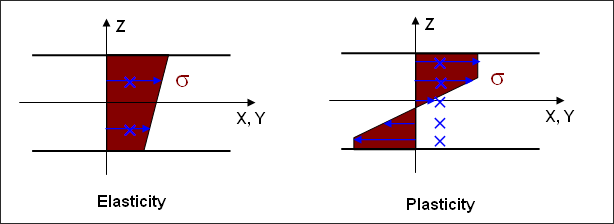
図 4. シェル断面の直応力分布

十分な精度を低いCPUコストで得る1つの方法はグローバル積分を用いることです。これはvon Mises塑性基準をいわゆるIlluyshin基準に変換することからなり、積分点での応力成分は内力（N、M、Tなど）に置き換えられます。

多層シェル要素では、それぞれの層の中心で1積分点が割り当てられます。

注: 2層のみの複合材では、更なる層を（全体の板厚に対して）十分な数の積分点数を得るために追加する必要があります。

図 5. 複合材の積分点数を定義する層定義

反復塑性投影

塑性の計算では、2つの基本的な仮定を満足する必要があります。最初に、塑性領域の応力は塑性の基準を検証する必要があります（例えば von Mises 基準）。2番目に、主応力空間で加工硬化による方向（$\text{Δ}\sigma$）は、降伏局面に直交することです。

デフォルトでは、ラジアルリターンが降伏局面に投影する応力テンソルに適用されます。この方法は良い方法ですが、塑性は近似で2番目の仮定が常に満足されるわけではありません（図 6）。反復直交投影も利用可能で、この方法では2番目の仮定も反復アルゴリズムにより満足させることができます（Radioss Theory ManualのShell Elementsを参照）。投影後の応力分布に高い精度が必要な場合には反復投影を用いてください。残留応力やスプリングバックが必要ならばこの場合になります。主応力成分の差が大きい時（例えば純せん断の場合）はラジアルリターンの誤差が高くなります。

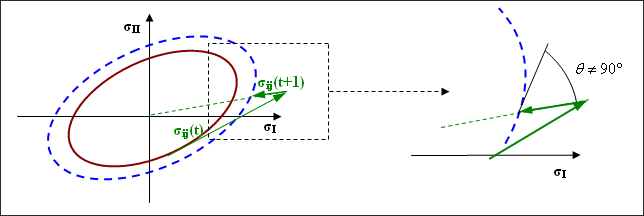
図 6. ラジアルリターン

板厚変化

デフォルトでは、シェルの板厚は変形の間一定として取り扱われます。初期板厚がひずみの計算と応力の積分に用いられますが、ポストプロセスの理由から板厚変化は計算されます。可変板厚（I_thick =1）が用いられた場合、真の板厚がポストプロセッシングだけでなく、ひずみの計算と応力積分にも用いられます。

コメント

1. 結果の精度のためには、特にネッキングまたはスプリングバックの時は、 反復塑性投影と板厚変化を用いることが強く推奨されます。