/MAT/LAW83

ブロックフォーマットのキーワードこの材料則は結合材料を記述します。この材料則を使用して、スポット溶接、溶接線、接着、または積層複合材料内の接着層をモデル化できます。

弾性挙動と弾塑性挙動を定義できます。材料の塑性挙動は、対応する変位速度に対して法線方向とせん断方向で結合できます。この材料は六面体ソリッド要素（/BRICK）にしか適用できず、要素時間ステップが要素高さに依存しません。

フォーマット

(1)	(2)	(3)	(5)	(6)	(7)	(9)
/MAT/LAW83/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$ $ρ_{i}$
`E`		`G`	`Imass`	`Icomp`	`Ecomp`
`fct_ID`₁		`Y_scale`₁	`X_scale`₁		α	$β$ $β$
`R`_N		`R`_S	`F`_smooth	`F`_cut
`fct_ID`_N	`fct_ID`_S	`XSCALE`

定義

フィールド	内容	SI単位の例
`mat_ID`	材料識別子（整数、最大10桁）
`unit_ID`	単位識別子。（整数、最大10桁）
`mat_title`	材料のタイトル（文字、最大100文字）
$ρ_{i}$ $ρ_{i}$	初期密度（実数）	$[\frac{kg}{m^{3}}]$ $[\frac{kg}{m^{3}}]$
`E`	引張状態における単位長さ毎のヤング（剛性）率（実数）	$[\frac{P a}{m}]$ $[\frac{P a}{m}]$
`G`	単位長さ毎のせん断（剛性）率デフォルト = `E` （実数）	$[\frac{P a}{m}]$ $[\frac{P a}{m}]$
`Imass`	質量計算フラグ = 0（デフォルト）要素質量は密度と体積を使用して計算される = 1 要素質量は密度と（上面と底面の平均）面積を使用して計算される（整数）
`Icomp`	圧縮挙動のフラグ。 = 0 引張と圧縮での対称弾塑性挙動 = 1 圧縮における線形弾性、引張における弾塑性挙動デフォルト = 0（整数）
`Ecomp`	圧縮状態における単位長さ毎のヤング率デフォルト = -E（実数）	$[\frac{P a}{m}]$ $[\frac{P a}{m}]$
`fct_ID`₁	真応力対塑性変位を指定する正規化された降伏曲線（整数）
`Y_scale`₁	正規化された関数`fct_ID`₁の縦軸のスケールファクター 10 デフォルト = 1.0（実数）
`X_scale`₁	`fct_ID`₁の横軸のスケールファクター 10 デフォルト = 1.0（実数）	$[m]$ $[m]$
$α$ $α$	有効な真応力の計算に使用されるパラメータ 8 デフォルト = 0.0（実数）
$β$ $β$	有効な真応力の計算に使用される指数 8 デフォルト = 2.0（実数）
`R`_N	有効な真応力の計算に使用される法線方向の最大真応力。デフォルト = 1.0（実数）	$[Pa]$ $[Pa]$
`R`_S	有効な真応力の計算に使用されるせん断方向の最大真応力。デフォルト = 1.0（実数）	$[Pa]$ $[Pa]$
`F`_smooth	変位速度フィルタリングフラグ = 0（デフォルト）変位速度フィルタリングなし = 1 変位速度フィルタリングあり（整数）
`F`_cut	変位速度フィルタリングのカットオフ周波数デフォルト = 10³⁰（実数）	$[Hz]$ $[Hz]$
`fct_ID`_N	スケールファクター対法線方向の塑性変位速度を定義する関数識別子。 9 デフォルト = 0（整数）
`fct_ID`_S	スケールファクター対せん断方向の塑性変位速度を定義する関数識別子。 9 デフォルト = 0（整数）
`XSCALE`	関数`fct_ID`_Nと`fct_ID`_Sの横軸のスケールファクター 9 デフォルト = 1.0（実数）	$[\frac{m}{s}]$ $[\frac{m}{s}]$

例（結合）

この例では、法線の降伏曲線はfct_ID₁=200です。最大法線真応力は0.2GPa、最大せん断真応力は0.4GPaです。

β = 2

$β = 2$ で、これは結合の混合モード荷重ケース（30°または60°）のフィッティングに使用します。

α = 0

$α = 0$ で、剥離効果は考慮されません。

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1 
unit for mat
                  kg                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW83/1/1
CONNECT MATERIAL
#              RHO_I
              7.8E-6
#                  E                   G     Imass     Icomp               Ecomp 
                  20                             0         0
#  Fct_ID1                      Y_scale1            X_scale1               ALPHA                BETA
       200                             1                   1                   0                   2
#                 RN                  RS   Fsmooth                Fcut
                  .2                  .4         0                   0
#  Fct_IDN   Fct_IDS              XSCALE
         0         0                   0
/FAIL/SNCONNECT/1/1
#            ALPHA_0              BETA_0             ALPHA_F              BETA_F  Ifail_so      ISYM
                   0                   2                   0                   2         1         1
#   Fct_0N    Fct_0S    Fct_FN    Fct_FS            XSCALE_0            XSCALE_F           AREAscale
      2001      2002      2003      2004                   1                   1                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/200
MAT83 curve
#                  X                   Y
                   0                   1                                                            
                   1                   1                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2001
Fct_0N
#                  X                   Y
                   0                  .5                                                            
                   1                  .5                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2002
Fct_0S
#                  X                   Y
                   0                  .5                                                            
                   1                  .5                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2003
Fct_fN
#                  X                   Y
                   0                   1                                                            
                   1                   1                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2004
Fct_fS
#                  X                   Y
                   0                   1                                                            
                   1                   1                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

この材料則は、8節点六面体要素（/BRICK）とのみ互換性があります。/PROP/TYPE43とのみ適合します。
剛性係数および降伏曲線：
- ソリッド要素の初期高さに依存しないようにするため、剛性係数および応力は変位毎に定義されます。
  例えば、 $E$ $E$ =210000 MPa/mmは、降伏応力曲線で指定された降伏応力の限度に達するまで、法線方向応力が1mm変位するごとに21000Pa増加することを意味します。
- せん断方向の剛性は、剛性係数 $E$ $E$ に等しいと見なされます（図 1）。
- ポアソン比は0です。
- 降伏応力（fct_ID₁1で定義）に達した後、材料は塑性相に移行します。最大応力R_N（引張）またはR_S（せん断）に達した後は、材料内の応力は増加しません（図 1）。
  
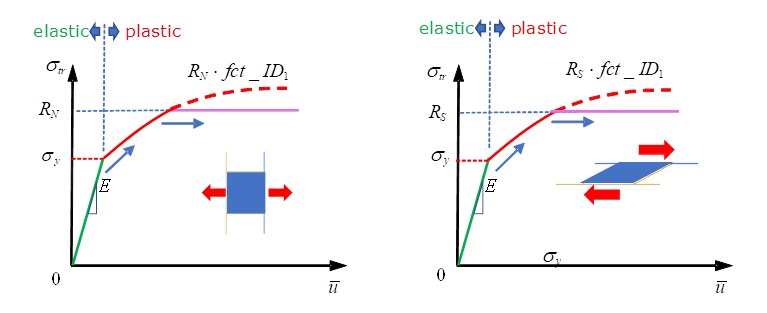
  図 1.
- 塑性の伸びは、fct_ID₁が指定されている場合に考慮されます。これは、通常、真応力を塑性変位の関数として表す、減少しない関数です。横軸の値の最初は “0”で、縦軸の値の最初は降伏応力であるべきです。関数は材料の損傷をモデル化する応力低下の部分を含む事もできます。
  
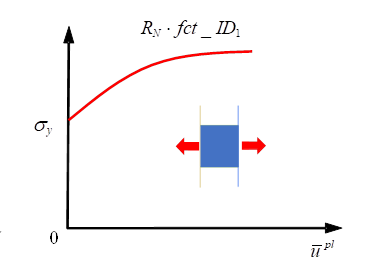
  図 2.
塑性変位。
完全な要素の変位 $¯ u$ $\bar{u}$ は弾性部分 ${¯ u}^{e}$ ${\bar{u}}^{e}$ （降伏応力に達する前）と塑性の変位の部分 ${¯ u}^{p l}$ ${\bar{u}}^{p l}$ に分割できます。単軸引張および圧縮の最も単純なケースでは、塑性変位は次の式で計算されます：(1)
${¯ u}^{p l} = ¯ u - {¯ u}^{e} = ¯ u - \frac{σ_{t r}}{E}$ ${\bar{u}}^{p l} = \bar{u} - {\bar{u}}^{e} = \bar{u} - \frac{σ_{t r}}{E}$

全法線変位は、塑性法線変位と弾性法線変位の和です。
材料挙動は、引張や圧縮と同じです。法線DOFとせん断DOFは、弾性領域で連成されません。
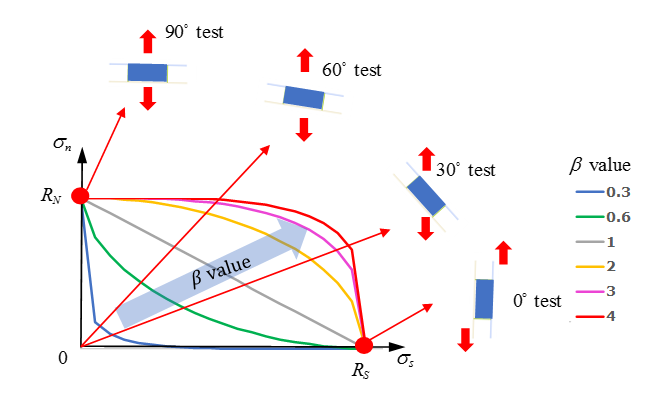
法線DOFとせん断DOFは、塑性領域で連成されます。正規化された有効な真応力（ $σ_{y}$ $σ_{y}$ ）は、法線（ $σ_{n}$ $σ_{n}$ ）とせん断応力（ $σ_{s}$ $σ_{s}$ ）から次のように計算されます：(2)
$σ_{y} = {[{(\frac{σ_{n}}{R_{N} \cdot f_{N} (1 - α \cdot sym)})}^{β} + {(\frac{σ_{s}}{R_{S} \cdot f_{S}})}^{β}]}^{\frac{1}{β}}$ $σ_{y} = {[{(\frac{σ_{n}}{R_{N} \cdot f_{N} (1 - α \cdot sym)})}^{β} + {(\frac{σ_{s}}{R_{S} \cdot f_{S}})}^{β}]}^{\frac{1}{β}}$

ここで、

$f_{N}$ $f_{N}$ および $f_{S}$ $f_{S}$

fct_ID_Nおよびfct_IDSの関数。

fct_ID_N および fct_ID_S

塑性変位速度の関数として法線応力とせん断応力のスケーリング係数を指定します。

$sym$ $sym$

$sin A$ $\sin A$

$A$ $A$

ソリッド要素の底面法線と上面法線の間の角度です。

図 3.

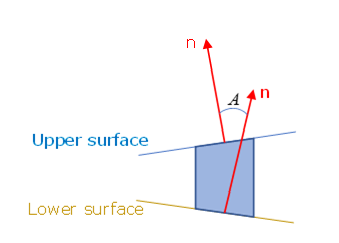
$α$ $α$

モーメントの影響を記述する（たとえば剥離試験における）ために用いられるスケールファクターです。

$β$ $β$

法線およびせん断の組み合わせ試験でフィッティングされることが可能です。たとえば、60°試験または30°試験。

パラメータ $β$ $β$ をフィッティングさせるには、少なくとも1つの組み合わせ試験が必要です。図 4 は、組み合わせ試験での最大応力に対する $β$ $β$ の影響を示しています。

図 4.
ソリッド要素の高さは0にすることができます。要素の高さは時間ステップに影響しません。この材料で使用できるのは、節点時間ステップのみです。
ソリッド要素のすべての節点が、他のシェルまたはソリッド要素か、剛体のセカンダリ節点（/RBODY）またはタイドインターフェースのセカンダリ節点（/INTER/TYPE2）に結合されている必要があります。
ソリッド要素のすべての節点が自由になると、その要素は削除されます。
この材料の破断基準は、/FAIL/SNCONNECTで定義されます。
真応力は、次のように、fct_ID₁から取得されます：(3)
$Y = Y_s c a l e_{1} \cdot f_{1} (\frac{X}{X_s c a l e_{1}})$ $Y = Y_s c a l e_{1} \cdot f_{1} (\frac{X}{X_s c a l e_{1}})$

ここで、 $f_{1}$ $f_{1}$ はfct_ID₁の関数

/MAT/LAW83

フォーマット

定義

例（結合）

コメント