Dynamic Aeroelastic Analysis
Dynamic Aeroelastic Analysis is the study of the deflection in flexible structures under aerodynamic loads, where the forces and acceleration are time dependent.
Flutter Analysis
Aeroelastic flutter is a dynamic instability of a structure associated with the interaction of aerodynamic, elastic, and inertial loads.
Flutter analysis of aeroelastic systems involves determining the velocity (and hence Mach Number) of the system and the frequency of oscillation at which the system attains the state of flutter. In this phenomenon, the aerodynamic loads on a flexible body couple with its natural modes of vibration to produce oscillatory motions with increasing amplitude.
This may lead to catastrophic structural failure. Therefore, structures exposed to aerodynamic loads must be carefully designed to avoid flutter.
In finite element analysis, the prediction of flutter involves a series of complex eigenvalue solutions. OptiStruct uses the modal approach where the structural-vibration modes in a selected frequency range are used as the degrees of freedom.
Methods
The four different methods for flutter analysis supported in OptiStruct are K, KE, PK and PKNL.
For each of these methods described below, the complex eigenvalues ( ) are extracted for a particular case, from which the pairs of airspeed and damping ( - ), and airspeed and frequency ( - ) can be ascertained.
The precise form of eigenvalues differs for each of the methods.
- Transient decay rate coefficient.
- Circular frequency, given by .
- K Method:
- The philosophy behind the K method is to inject the system with artificial damping (in the form of a structural damping term) to push the system to the flutter point.
- A set of complex eigenvalues is output at every combination of density, Mach number, and reduced frequency from the FLFACT entries.
- For this reason, the results obtained from the K method are slightly difficult to interpret.
- KE Method:
- The KE method is a variant of the
K method with the following differences.
- The viscous damping terms are ignored.
- The complex modes are not output.
- The flutter output is arranged based on modes and sorted using an eigenvalue extrapolation technique.
- These features imply that the KE method is a computationally inexpensive and easy-to-interpret version of the K method.
- The KE method is a variant of the
K method with the following differences.
- PK Method:
- The PK method allows for a general flutter analysis to be performed using doublet lattice aerodynamics (that assumes simple harmonic motion) using an iterative process.
- In this method, the imaginary contributions to the stiffness matrix are ignored. This means that structural damping terms and modal damping with PARAM, KDAMP, -1 will not be taken into account.
- The eigenvalue extraction is carried out for every combination of density, Mach number, and velocity from the FLFACT entries.
- An initial guess of the reduced frequency ( ) is used to solve the complex eigen problem whose output returns an updated reduced frequency; the process being repeated until convergence. Modes are tracked across airspeeds using the left and right complex eigenvectors.
- PKNL Method:
- The PKNL method is a variant of the PK method designed with ‘no looping’.
- In this method, the number of entries in the FLFACT data for density ratios, Mach numbers, and velocities need to be the same and the eigenvalue extraction is carried out at each linear selection of density ratio, Mach number, and velocity.
- Scenario 1: The flutter analysis is carried out at the following points: (0.5, 0.3, 100), (0.5, 0.3, 200), (1.0, 0.3, 100), (1.0, 0.3, 200), (0.5, 0.4, 100), (0.5, 0.4, 200), (1.0, 0.4, 100) and (1.0, 0.4, 200).
$--1---><---2--><---3--><---4--><--5---><--6---><---7--><--8---><---9--> FLUTTER 103 PK 1 2 3 L 4 FLFACT 1 0.5 1.0 FLFACT 2 0.3 0.4 FLFACT 3 100.0 200.0 - Scenario 2: The flutter analysis is carried out at the following points: (0.5, 0.3, 100) and (1.0, 0.4, 200).
$--1---><---2--><---3--><---4--><--5---><--6---><---7--><--8---><---9--> FLUTTER 103 PKNL 1 2 3 L 4 FLFACT 1 0.5 1.0 FLFACT 2 0.3 0.4 FLFACT 3 100.0 200.0
Input
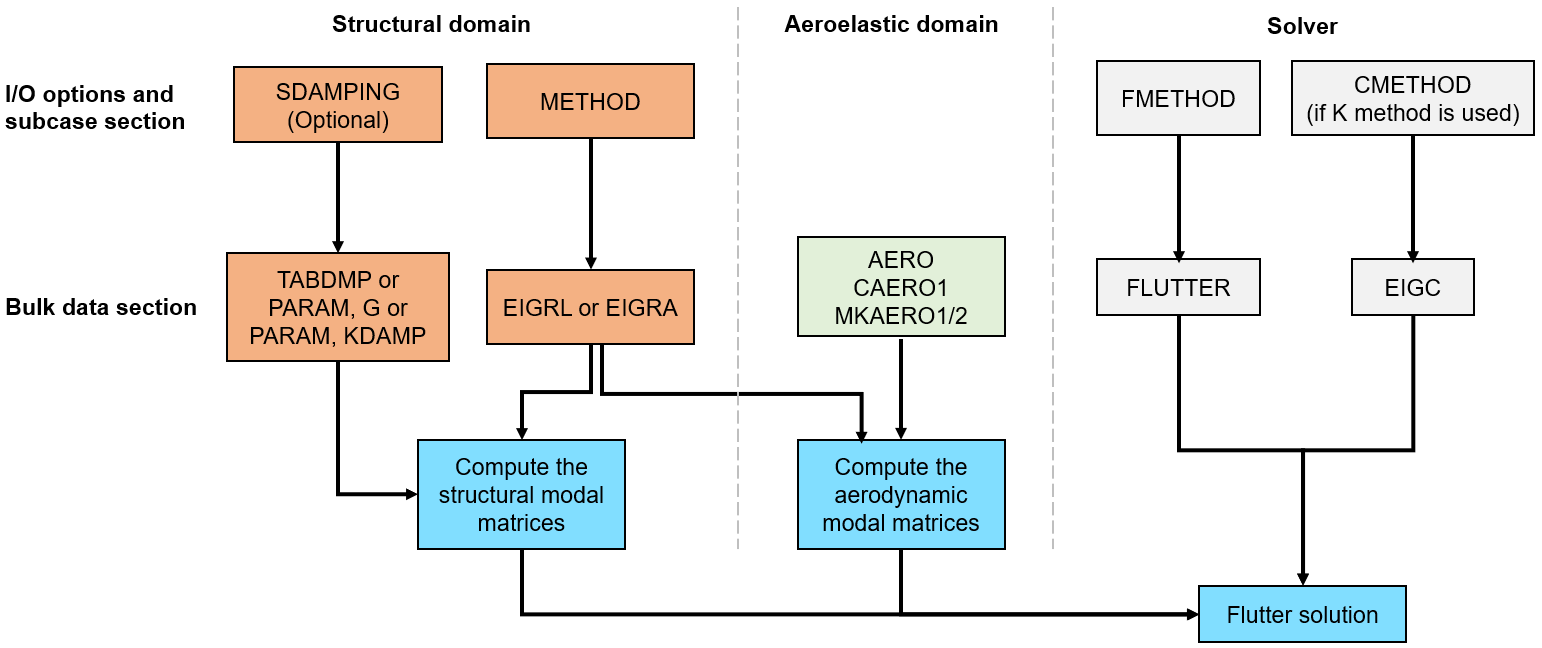
Figure 1. Flutter analysis workflow
| Entry | Description |
|---|---|
| AERO | Defines flight conditions. |
| MKAERO1/MKAERO2 | Specifies the Mach number and reduced frequency pairs for the explicit computation of the aerodynamic matrix. |
| FLFACT | Specifies the values of flutter parameters (Density ratios, velocities, and reduced frequencies) for flutter analysis. |
| FLUTTER | Selects the method (K/KE/PK/PKNL) and parameters for flutter analysis. This entry also references the definitions of FLFACT. |
| EIGC | Selects the complex eigenvalue method for the K method. |
| EIGRL/EIGRA |
|
| PARAM, VREF | Used to scale the output velocity: Vout = V/Vref. |
| DMI | Defines real matrix data blocks. |
Problem Setup
$ ************************************************************
$ SNIPPET OF AN INPUT FILE FOR AEROELASTIC FLUTTER ANALYSIS
$ ************************************************************
SUBCASE 101
SPC = 101
METHOD = 102
FMETHOD = 103
CMETHOD = 104
BEGIN BULK
$--1---><--2---><--3---><--4---><--5---><--6---><--7---><--8---><--9---><--10-->
EIGRL 1 0.0 100. 4 MASS
EIGC 109
FLUTTER 103 K 1 2 3 L 4
FLFACT 1 0.1
FLFACT 2 .90
FLFACT 3 0.001 0.18 0.26 0.34 0.6
AERO 102890. 2200. .123E-110 0
MKAERO1 0.3 +
+ 0.01000 0.03359 0.06717 0.20152 0.33587 0.47022 0.60456 0.67174
$ other aeroelastic and structural entriesOutput
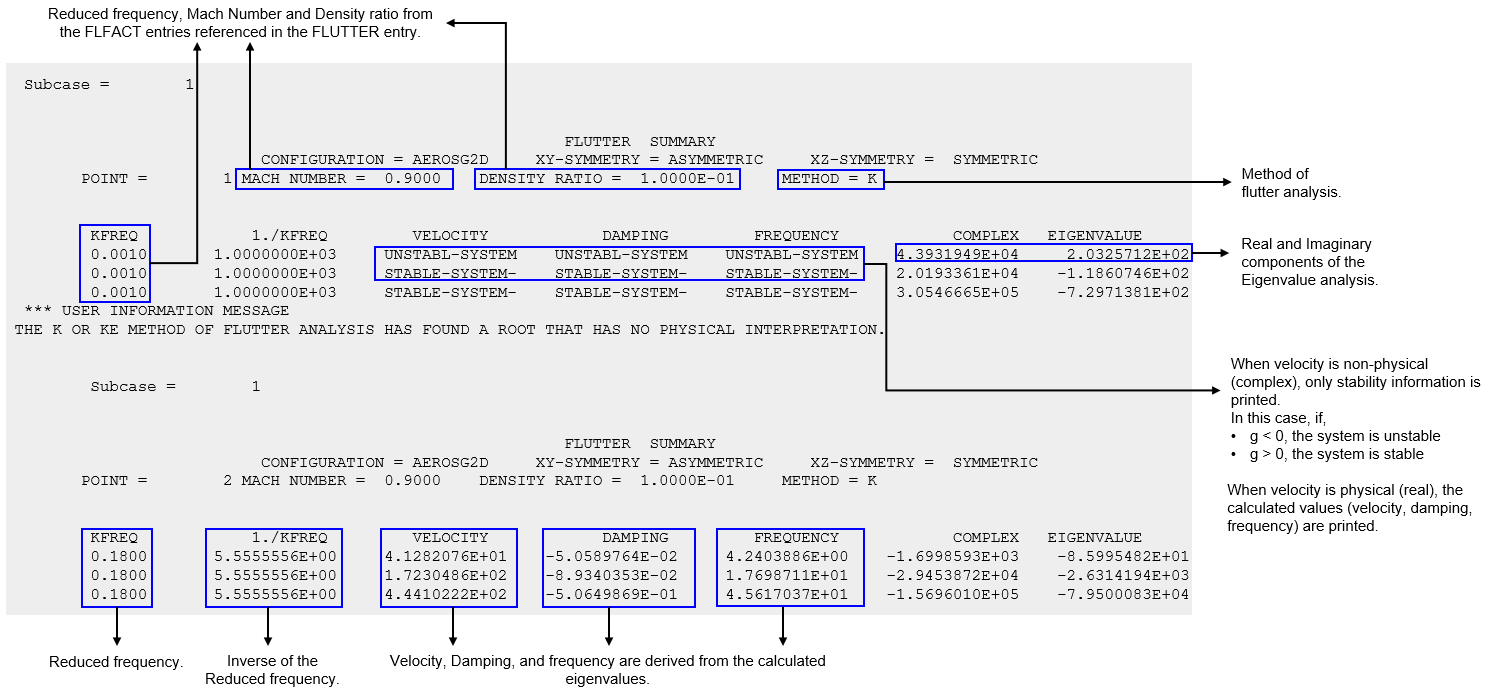
Figure 2. Flutter analysis summary in an example .flt file
- The eigenvalue (
) is used to determine airspeed (
) and damping (
) using Equation 1. Note: This equation can be split into two equations for real and imaginary components and the two unknowns can be solved.
- When the values of are such that is physical (real), the calculated values of velocity, damping and frequency are printed.
- When the values of are such that is non-physical (complex), only stability information is printed for velocity, damping, and frequency values.
- In such cases, when
- g < 0
- the system is unstable
- g > 0
- the system is stable
- The determined values of
in conjunction with the user-specified
reduced frequency (
) and reference chord length
(REFC from AERO entry) can
be used to calculate the frequency (
),
(3) Using the calculated from Equation 3,(4) - Since the KE method arranges the flutter summary by mode, the flutter point can be easily ascertained from a visual inspection of when the damping switches signs.
- The frequency (
) and damping (
) are extracted from the form of the eigen
value using Equation 2. Note: This equation can be split into two equations for real and imaginary components and the two unknowns can be solved.
The damping reported is:
(5) - In the case of purely real roots, the damping is:
(6)
The .flt file can be loaded into the “Flutter Curves” functionality of the aeroelasticity module of HyperWorks to easily generate the ( - ) and ( - ) curves without the use of any external post-processing tool.
Flutter Analysis Output
- DISPLACEMENT (also with Modal option)
- SDISPLACEMENT - available only for K, PK and PKNL methods
| Method | Comments |
|---|---|
| K Method |
|
| KE Method |
|
| PK/PKNL Method |
|