タイヤ接触法

タイヤの接触計算では、タイヤ貫通量や接触パッチ位置などを計算します。その結果は、タイヤモデルでフォースとモーメントを計算するために使用します。MotionSolveでは、次の2つの接触法を使用できます：
  • 単点接触
  • 楕円カム接触モデル

タイヤのプロパティファイルの[MODEL]ブロックに'CONTACT_MODEL'キーが存在しない場合、単一点接触方式が使用されます。カム接触方式を選択するには、[MODEL]ブロックの以下のキーバリューを使用します。

CONTACT_MODEL = ‘3D_ENVELOPING’

注: タイヤのカーカス形状に関する追加情報をタイヤプロパティファイルで用意できます。上記のどちらの接触法でも、カーカス形状を考慮して接触パッチの位置を計算します。

単点接触

Fialaモデルで使用するデフォルトの接触法です。このモデルでは、タイヤとリムが“ディスク”形状であると見なし、ホイール平面とホイールに対する路面上の接線との交差位置となる接触点を計算します。

オートバイのタイヤは、自動車のタイヤよりも大きな曲率を持っています。車体が傾斜した状態では、理論的な接触点が横方向に移動します。この挙動をモデル化するために、タイヤのカーカス形状を使用します。



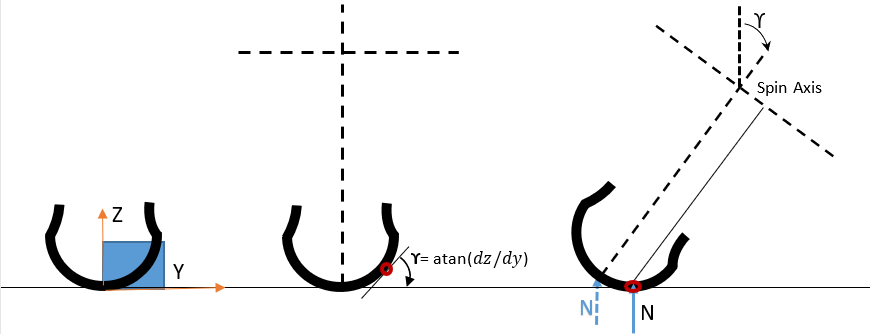
図 1. 左図：接触点の評価に必要なタイヤ断面データ、中央の図： キャンバー角が0の状態のタイヤ、右図： Y方向にキャンバー角が発生しているタイヤ

SECTION_PROFILE_TABLEは、タイヤのカーカスのデータを記述しています。この表は、下記のように2つの列で構成する必要があります。



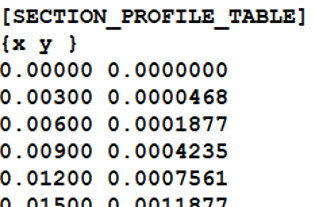
上記の表にある{x y}は、ラベルとして機能します。この表はTYDEX-W座標系に従って読み取られ、カーカスの幅方向の各点におけるカーカス高さの変化を表します。ISO座標系では、タイヤはXY平面を中心として対称であると見なされるので、タイヤのカーカス形状では、全体の1/4のデータがあれば十分です。。座標値が単調に増加するようにデータポイントを選択する必要があります。そのように選択しなかった場合、データポイントは無視され、タイヤのカーカスが矩形形状であると見なしてタイヤと地面との接触が計算されます。

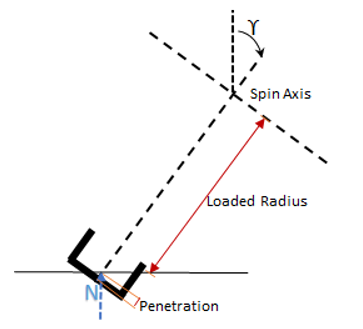
タイヤのプロパティファイルにSECTION_PROFILE_TABLEが存在しない場合は、カーカスが矩形形状であると想定されます。それは乗用車の場合で、タイヤのカーカスはほぼ矩形です。


図 2. カーカスの形状によらない単一点接触方式

接触パッチ寸法PA1とPA2は、接触パッチの長さの変化を表しています。接触パッチのサイズは、垂直荷重の増加に伴って増加します。接触パッチの寸法は、タイヤをカーボン紙に押しつけるか、インクを使用することによって取得できます。

接触長さの方程式：
パラメータ 内容 単位
PA1 接触長さ方程式の平方根項の係数。 -
PA2 接触長さ方程式の線形項の係数。 -

タイヤのプロパティファイルの[PARAMETER]ブロックに上記のパラメーターがある場合、接触パッチ長さを以下のように評価します。

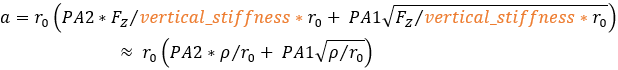
ここで、 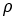はタイヤの貫通量、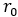は無荷重状態にあるタイヤの半径です。

PA1、PA2パラメータが見つからない場合は、タイヤを無荷重半径と同じ半径の剛体ディスクと仮定し、接触パッチ長を以下のように評価します。



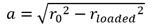
接触幅の方程式：

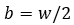
ここで、aとbは、それぞれ接触パッチの有効長さと有効幅の半分の値です。

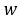はタイヤの幅です。

楕円カム接触モデル

接触パッチより短い障害物上でのタイヤの非線形転がり挙動を予測するために、接触パッチ全体に分散された一連のパラレルカムを使用して形状フィルタを作成します。これらのカムは、路面の高さ変動に従って上下に変位します。カムの中心を使用して、有効路面平面と呼ばれる仮想平面を作成します。この有効路面平面の向きは、タイヤに作用するとして得られたフォースが有効路面平面に垂直な方向を向くように定義されます。路面の次の特性が収集されます。
  • 有効路面高さ変動
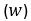
  • 有効傾斜変動
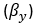
  • 有効曲率
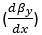
  • キャンバー変化
3D配置は、以下の図のようになります。


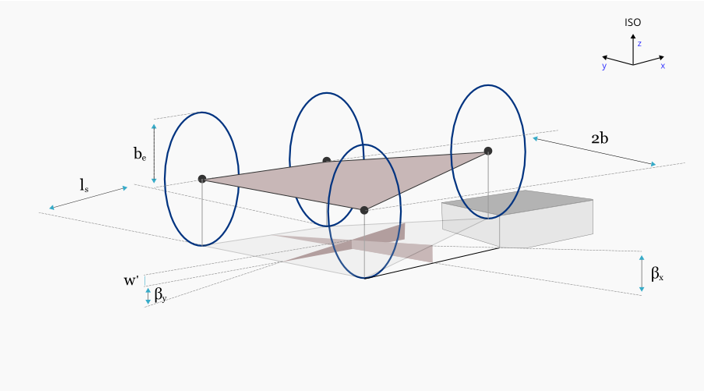
図 3. 3D楕円カム接触配置
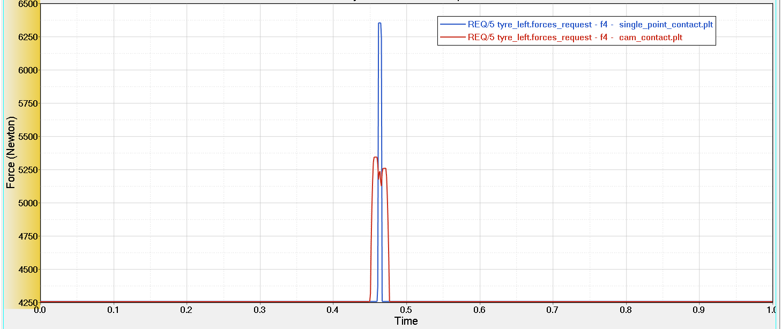
上記変動に基づき、FIALAアルゴリズムを使用してフォースを計算します。以下の図は、単一点接触を使用した場合に計算したフォースと、カム接触モデルを使用した場合に計算したフォースの違いを示しています。


図 4. タイヤが10.833 m/sec（39 km/h）の一定速度でクリート（高さ10 mm、長さ50 mm）上を転がる場合の一定アクスル高での垂直力


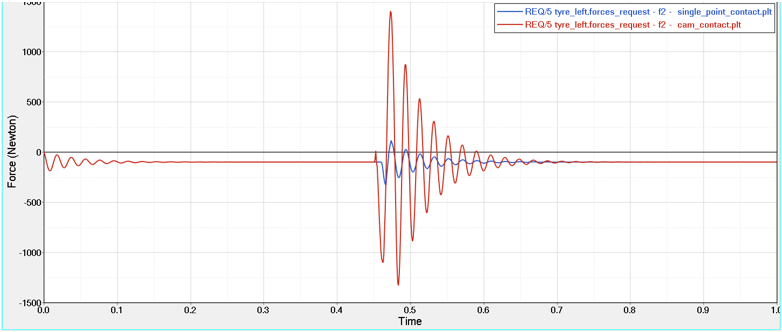
図 5. タイヤが10.833 m/sec（39 km/h）の一定速度でクリート（高さ10 mm、長さ50 mm）上を転がる場合の一定アクスル高での縦方向力

この結果は、単一点接触モデルの方が強い垂直力が発生することを予測していますが、これは障害物の形状をたどっているからです。タイヤが実際に受けるフォースは、カム接触法を使用して予測した値に近くなります。

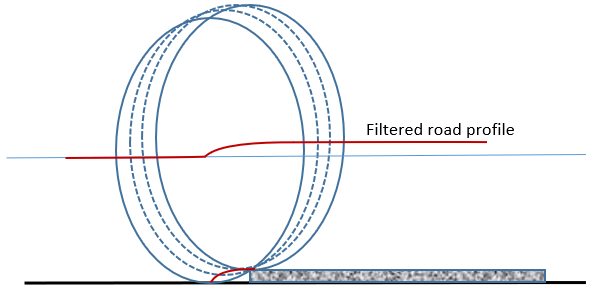
障害物の上を転がる場合のタイヤの外側の輪郭は、楕円形状に近くなります。実際、輪郭を測定することにより、カム接触モデルに必要な楕円寸法を決定できます。


図 6. 一連のカムを使用して絞り込まれた路面プロファイル

カム接触モデルの使用方法

FIALAタイヤでカム接触法を使用するには、次の属性が[MODEL]ブロックに存在する必要があります。

CONTACT_MODEL = '3D_ENVELOPING'

[MODEL]ブロックに'CONTACT_MODEL'属性が存在しない場合、FIALAタイヤでは単一点接触法が使用されます。この属性を'3D_ENVELOPING'に設定している場合は、タイヤインターフェースで[CONTACT_COEFFICIENTS]ブロックが検索されます。このブロックには下の表に示すパラメータを記述する必要があります。
パラメータ 詳細 単位
PA1 接触長さ方程式の平方根項の係数。 -
PA2 接触長さ方程式の線形項の係数。 -
PAE 楕円体の半値長さ。 長さ
PBE 楕円体の半値高さ。 長さ
PCE 楕円体の順序。 -
PLS 前方の楕円体と後方の楕円体間の距離のスケーリング。 -
ROAD_INCREMENT 楕円体のメッシュサイズ。 長さ
N_WIDTH 接触幅方向のカムの数。 -
N_LENGTH 接触長さ方向のカムの数。 -
MESH_HEIGHT 楕円メッシュの端点の高さ。障害物高さより大きくする必要があります。  

PA1とPA2は、接触パッチの長さの変化を表しています。接触パッチのサイズは、垂直荷重の増加に伴って増加します。接触パッチの寸法は、タイヤをカーボン紙に押しつけるか、インクを使用することによって取得できます。

接触長さの方程式：

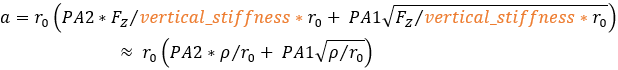
ここで、 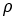はタイヤの貫通量、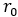は無荷重状態にあるタイヤの半径です。

接触幅の方程式：

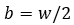
ここで、aとbは、それぞれ接触パッチの有効長さと有効幅の半分の値です。

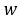はタイヤの幅です。

カムの形状に関する方程式は次のように記述できます。



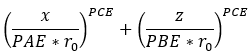
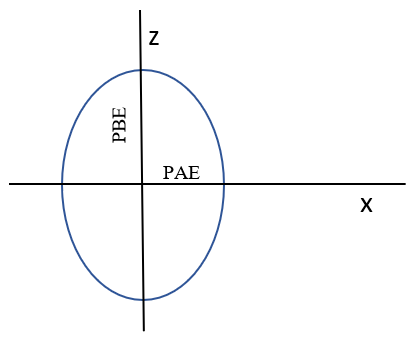
図 7. カム寸法


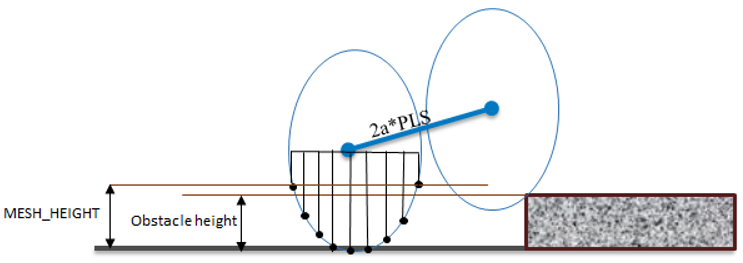
図 8. 2点フォロワーを備えたカム

データがない場合は、PAEとPBEがタイヤ半径に等しいと見なします。この楕円寸法は、タイヤが障害物と接触したときの外側の輪郭を測定することによって計算できます。PLSの場合は、0.8を適切な値として使用できます。ROAD_INCREMENTによって、路面のメッシングサイズが決まります。このサイズはモデルの計算時間に直接影響します。