メッシュ化コイル領域
概要
Fluxのメッシュ化コイルは、フェイスタイプ(2Dの場合)またはボリュームタイプ(3Dの場合)の領域であり、巻線をはじめとして、電流が流れる導体の表現に使用します。トピックFluxにおけるコイルと巻線で取り上げたように、これらの領域は外部電気回路との境界を提供し、有限要素ドメインに全面的に統合されています。したがって、Fluxでは、これらの領域で使用できるメッシュを活用して、導体全体で電磁的量(磁束密度、電流密度、ジュール損失密度など)を評価できます。
電流は磁気誘導の発生源であることから、電磁デバイスの設計では、コイル内部での電流密度分布の正確な評価がきわめて重要です。さらに、この量の高精度な計算は、ジュール損失の予測で重要な役割を果たします。一方、この分布を求めることは難度が高い処理になります。導電媒体では、表皮効果や近接効果をはじめとして、よく知られた電流集中現象が発生するからです。
- コイルと巻線の電流密度分布の不均一性につながる物理現象の概要
- 均質化手法とそれが巻線と導体のモデル化で持つ重要性の簡単な説明
- Fluxで使用できる2種類のメッシュ化コイル領域であるコイル導体領域とソリッド導体領域の比較解析
表皮効果と近接効果
コイルに電流を流すと、一般的にはコイルの導体全体を流れる電流の密度分布が不均一になります。
導体内部の電流密度分布には次のパラメータが影響します:
- 導体の導電率
- 導体の透磁率
- 電流の対時間変化速度
物理学と電気工学では、上記のパラメータに結び付けて電流集中現象を説明するために表皮効果という用語を使用します。この用語は次のような事実に基づいています。周波数 の正弦波で励磁されている導体で、次の式で求められる長さ を考えます。
この長さは導体表面からの深さであり、この深さに一定量の電流が集中していることを示しています。この長さを表皮深さと呼び、総電流の約95%(1-e-3)が、導体内部で表面から の3倍以内の深さの部分のみを流れていると考えられます。
表皮効果は、コイルを流れる誘導電流密度成分に置き換えて解釈できます。この誘導成分によって総合的な電流密度分布が変化します。誘導に関するファラデーの法則による予測に従い、適用した電流で発生する磁束密度の変化を打ち消す方向に誘導電流が発生します。図 1は、1mm2の円形断面を持つ銅導体に振幅1mAの正弦波電流を流したとき、周波数が高くなるに伴って現れる表皮効果の例を示しています。
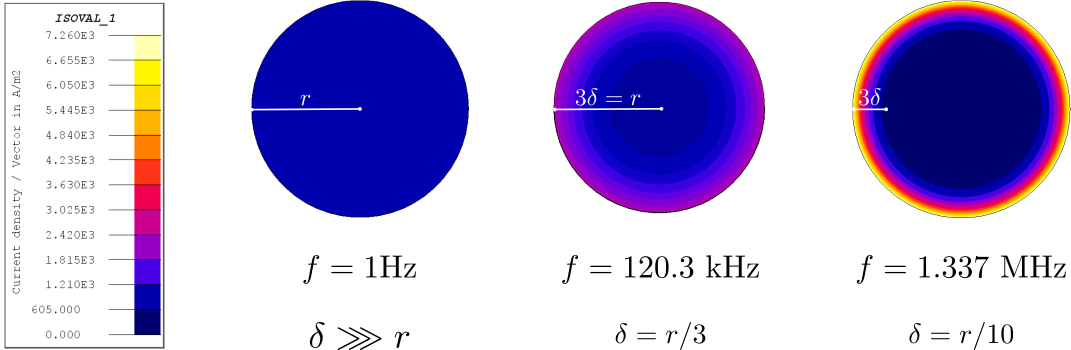
図 1. 周波数の上昇(表皮深さの減少)に伴い、円形銅導体の断面で見た電流密度分布に影響する表皮効果
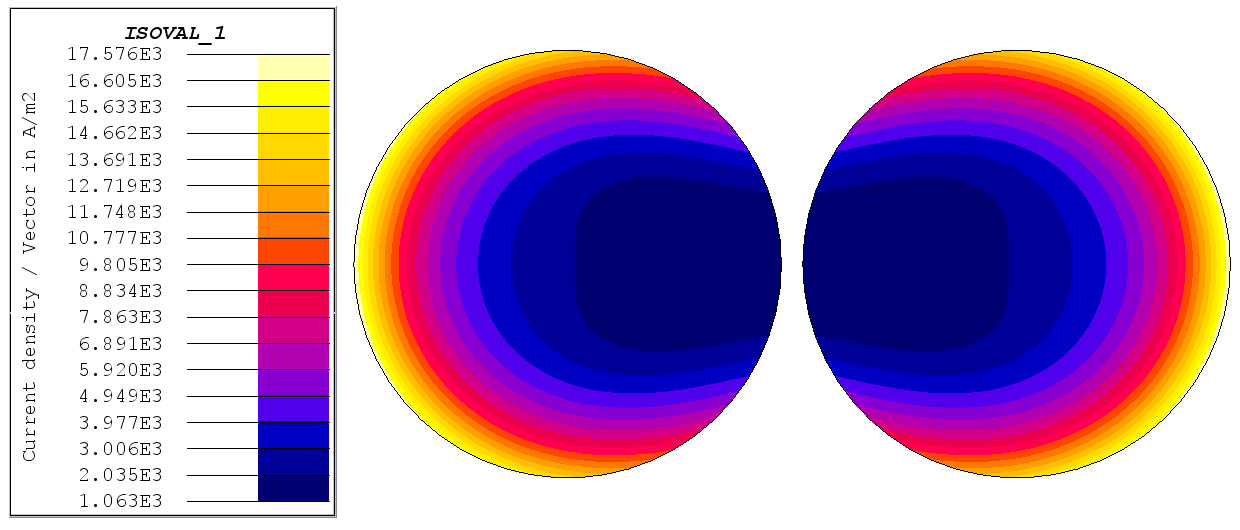
図 2. 平行に隣接配置した2本の円形導体の断面で見た電流密度分布に影響する近接効果。この例では、両方の導体を流れる電流は同方向の正弦波電流。
Fluxの均質化手法
細い多芯導体や巻数が数回のコイルで発生する損失を有限要素法で評価するには多大な手間を要することがあります。詳細な形状を使用してデバイスをメッシュ化する必要があるからです。よく知られた経験則では、導体表面から1番目または2番目の表皮深さに相当する範囲を詳しく離散化することが推奨されています。しかし、この基準を満足するには、複雑なメッシュと大量のメモリが必要となることが普通です。特に3Dや高周波域で、この傾向が強くなります。
Fluxでは、2種類のメッシュ化コイル領域としてソリッド導体領域とコイル導体領域を用意することにより、メッシュの複雑さ、コンピューターリソースの使用量、精度とのトレードオフを扱っています。
電流が流れる個々の導体やコイルが持つ形状の複雑さをすべて表現する場合、Fluxではソリッド導体領域を使用します。この方法は、表皮効果と近接効果を厳密に考慮できるので、導体内部の電流密度分布の詳しいマッピングが必要な場合に効果的です。一方で、形状と回路の記述に手間を要するうえ、メッシュが複雑になりやすいので、メモリの使用量が増加し、演算時間も比較的長くなります。
それに対して、コイル導体領域は緊密に巻いた巻線に適しています。このような各巻線の配置は、固定モチーフまたはユニットセルを平行に配置することによって得られます。Fluxでは、この領域でユニットセルに対する事前計算を実行し、電流密度分布に対する表皮効果と近接効果の影響を推定します。この事前計算で得られた結果を、コイル導体領域に割り当てる材料の等価な特性に変換します。これらの基本セルに関する情報は、検討をご覧ください。
これらの領域ではフォイルコイルの巻線(金属導電シートを巻いたもの)も記述できます。この均質化タイプでは、Fluxは専用の式を使用して、電流密度分布における表皮効果と近接効果の影響を計算します。したがって、同じタイプのモデル化が存在しないので、ポスト処理で使用可能な量がさまざまに異なる可能性があります。このモデルの詳細については、検討をご覧ください。
上記の手法によって、巻線の表現を均質化(形状記述を簡素化)し、ソリッド導体領域に関連して発生していた前述の困難を回避します。ただし、均質化していない表現と均質化した表現との等価性は絶対的ではない点に注意が必要です。均質化ではジュール損失と保存されている磁気エネルギーが保持されますが、評価で得られた電流密度分布は異なるものになります。言い換えると、均質化したコイル導体領域で計算した電流密度分布は、ソリッド導体領域に基づくモデルで予測した電流密度分布と同じにはなりません。
次の項では、ソリッド導体領域とコイル導体領域を使用して簡潔な巻線をモデル化して結果を比較し、このような特徴を明確にします。
Fluxでのソリッド導体領域とコイル導体領域の比較
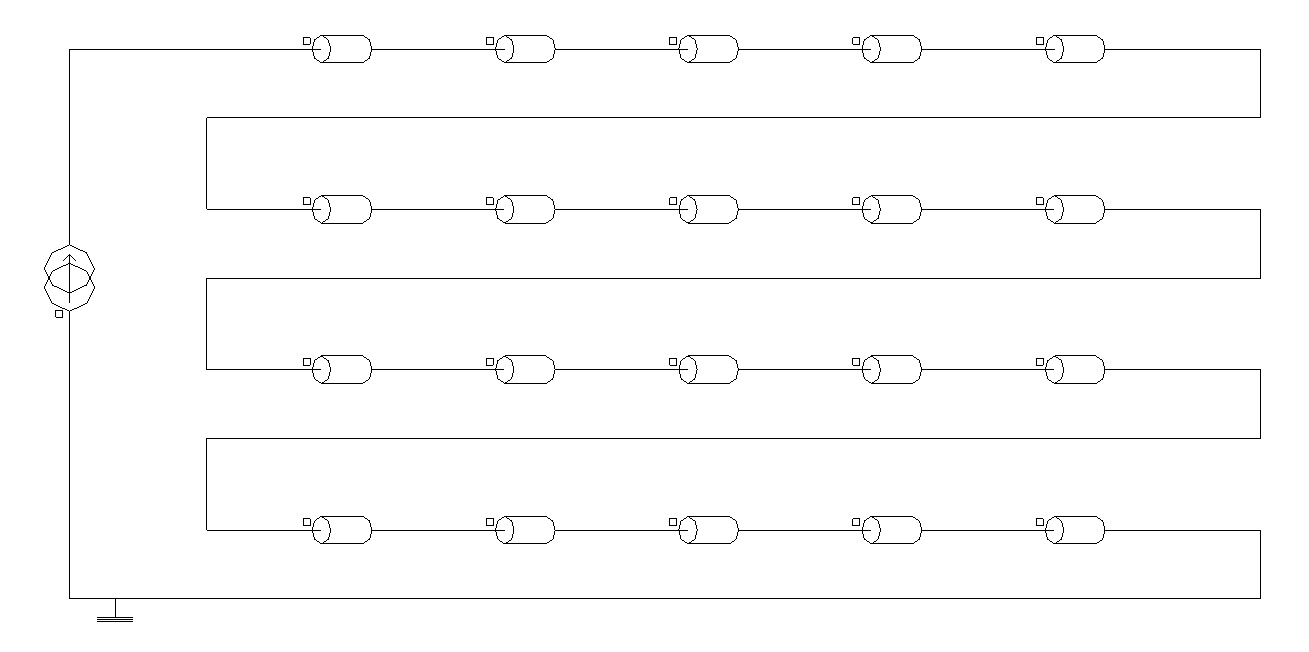
ソリッド導体領域を使用した場合とコイル導体領域を使用した場合を比較するために、仮想の誘導加熱デバイスをFlux 2Dでモデル化することを考えます。このデバイスには、線形強磁性体構造と銅板を磁化する巻数20のコイルを使用します。このコイル自体は円形断面の銅導体で形成し、高周波電流源から給電します。
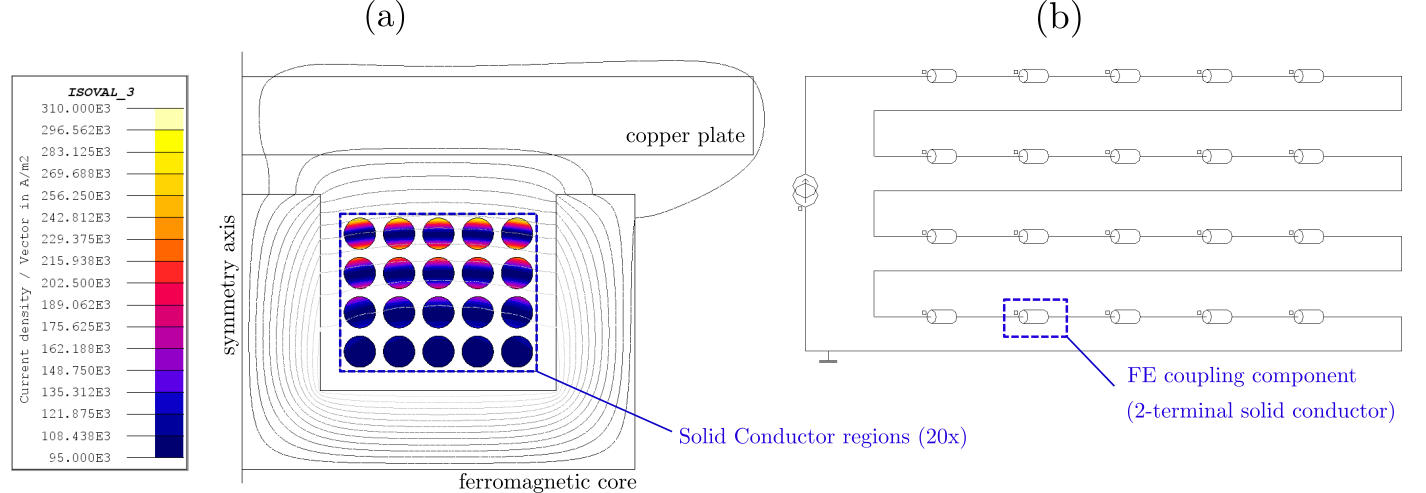
図 3. 1kHzで動作する仮想の誘導加熱デバイスに使用している巻数20のコイルをモデル化するFlux 2Dプロジェクト。各コイル巻線をソリッド導体領域に割り当て。(a)は、表皮効果と近接効果による複合的影響を受ける巻線の電流密度分布。(b)は、ソリッド導体領域ごとに1つのFE連成コンポーネントを持つ連成電気回路。
図 4は、上記と異なり、別の方法でモデル化した同じデバイスを示しています。形状には20本の巻線が個別には表示されなくなり、巻線を包含した矩形サーフェスに単一のコイル導体領域が割り当てられています。したがって、必要なFE連成コンポーネント(より線コイル導体タイプ)は1つのみで、形状記述と外部回路の表現の両方が簡潔になっています。
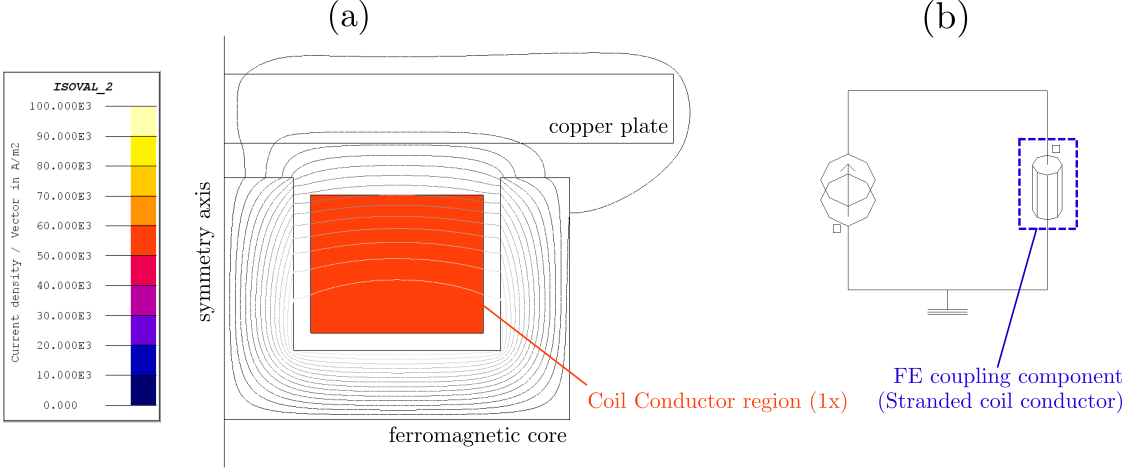
図 4. 1kHzで動作する同じ誘導加熱デバイスを、単一のコイル導体領域を使用してFlux 2Dでモデル化。この方法では、コイル導体領域内部の均一な等価電流密度をFluxで評価。前述のモデル化とは異なり、モデルの形状記述と外部回路(b)が簡潔。
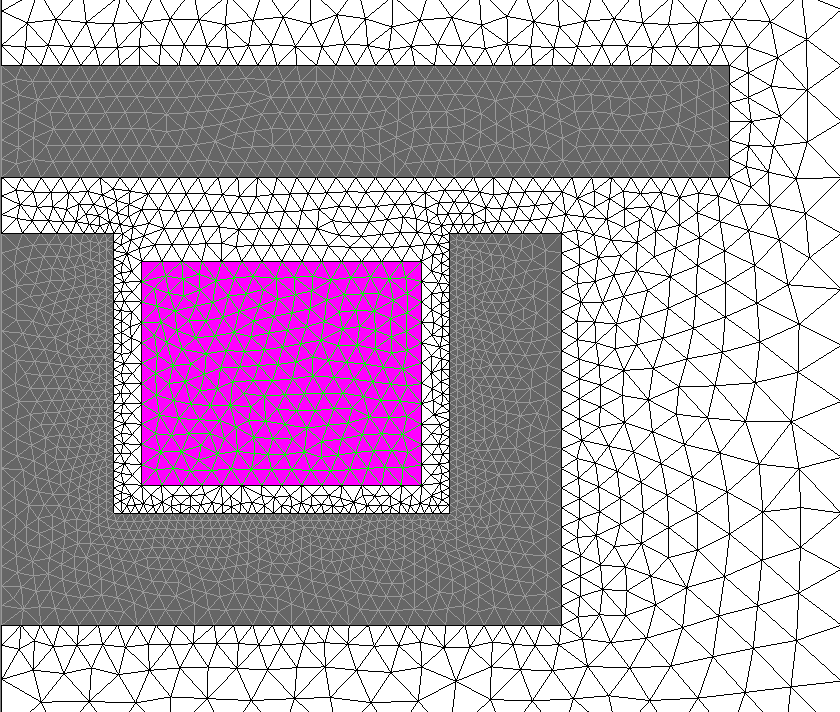
コイル導体領域による手法を使用することで、図 5に示すようにメッシュも簡潔になっています(同時に、必要とするメモリ量が少なくなり、演算時間も短くなります)。
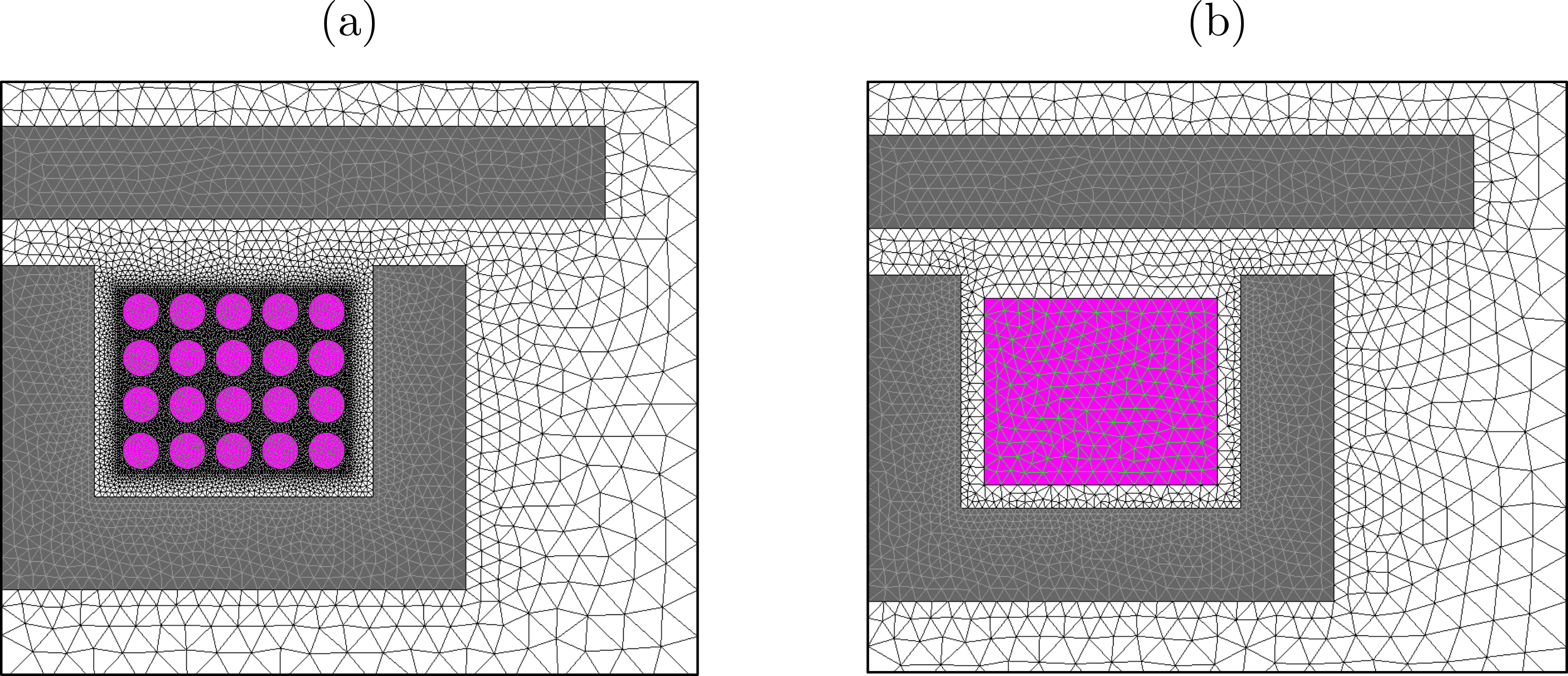
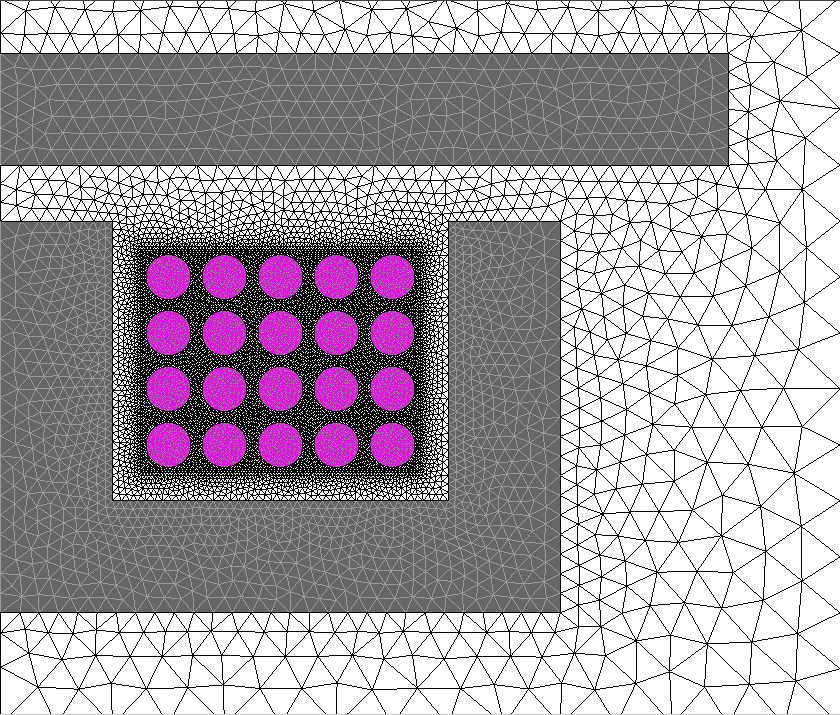
図 5. 2種類のモデル化手法で誘導加熱デバイスを離散化したメッシュの比較。(a)では、コイル巻線を形状にすべて記述し、それぞれをソリッド導体領域に割り当て。(b)では、巻線を包含した矩形フェイスに単一のコイル導体領域を割り当て。
コイル導体領域に基づく手法には、次の3点の可能性が生まれることに注目します:
- (a)コイル導体領域を作成するときに、巻線のユニットセルの詳しい記述を指定できます。この記述では、導体材料、巻線の巻数、巻線断面の形状と寸法、巻線間隔、コイルのフィルファクターなどのパラメータを指定します。この場合は、前の項で説明した均質化手順がFluxによって適用され、近接効果と表皮効果が考慮されます。コイル導体領域で評価した損失は、複数のソリッド導体領域を使用した最初のモデル化手法で予測した、図 6に示す周波数特性に従います。
- (b)詳しい記述ではなく、導体材料、巻線巻数、フィルファクターのみで構成した簡潔な記述を巻線に指定できます。この条件では、Fluxは巻線の均質化を実行できません。したがって、コイルでの表皮効果と近接効果は考慮されず、コイル導体領域で評価した損失は直流または低周波数による励磁でのみ正確です。この挙動は、図 6でも確認できます。
- (c)巻線の巻数のみを指定して、さらに簡潔な巻線の記述とすることもできます。コイル導体領域への材料の割り当ては任意となり、結果には影響しません。この状態は理想的な導体に相当し、コイル導体領域で評価した損失はすべての周波数でゼロになります(図 6では、ゼロワットで一定の水平線で表現されています)。
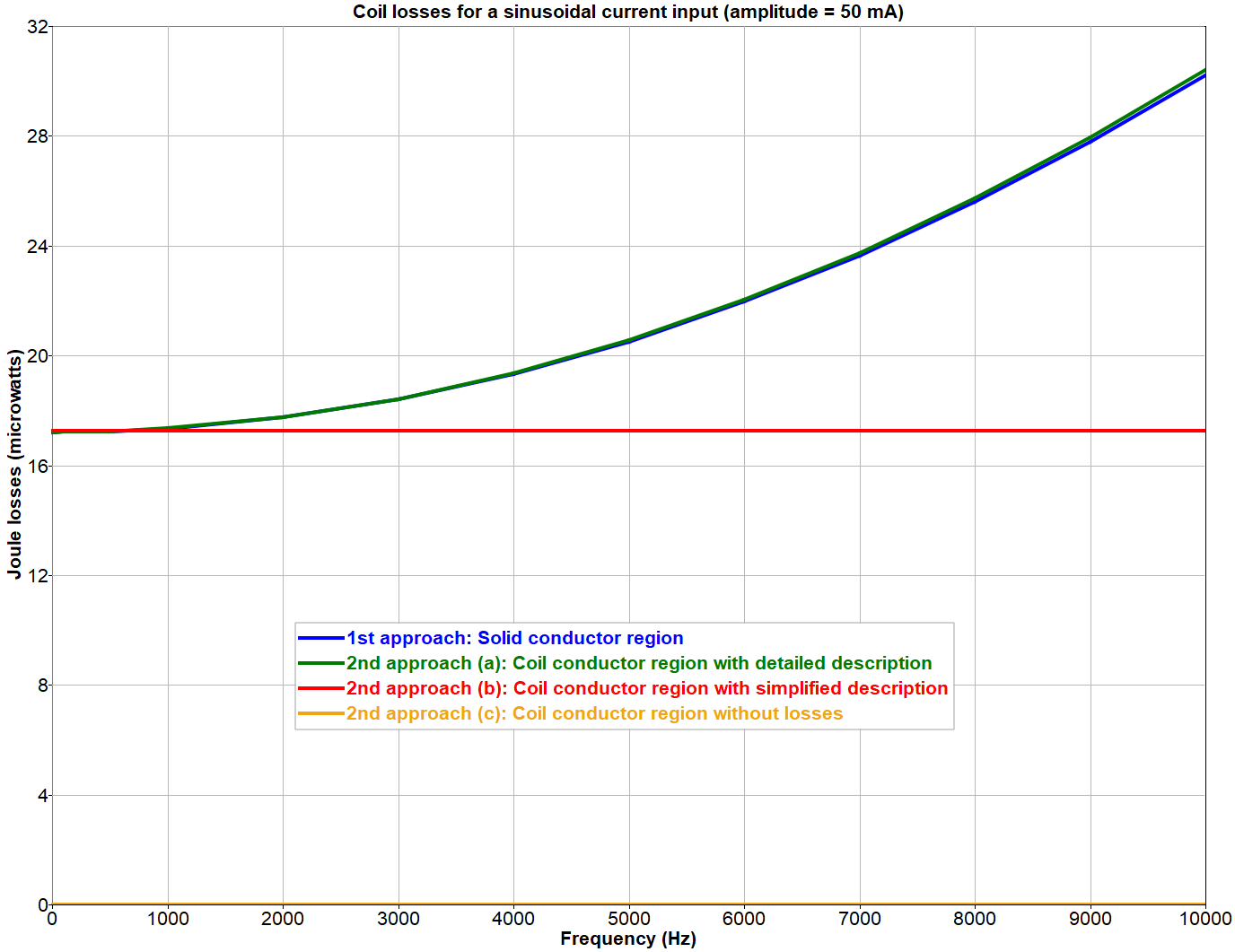
図 6. さまざまなモデル化手法によってFluxで得られたジュール損失の周波数特性の比較。
サマリー
| メッシュ化コイル領域タイプ | 電流密度 | メッシュ | 連成電気回路の記述 | ジュール損失の周波数特性 |
|---|---|---|---|---|
| ソリッド導体 | 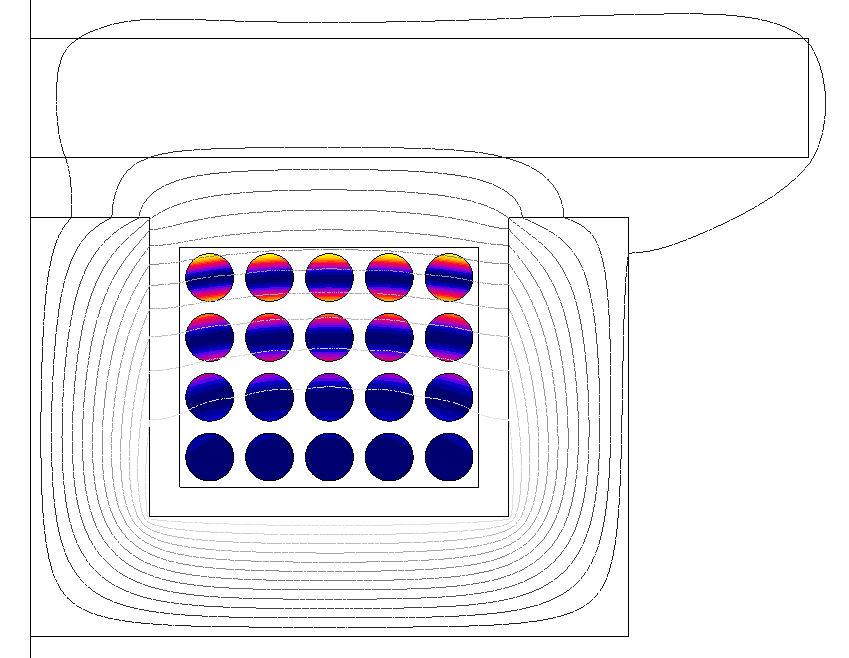 |
 複雑なメッシュが必要。 |
 手間を要する作業になる可能性あり。ソリッド導体領域ごとにFE連成コンポーネントが1つ必要。 |
表皮効果と近接効果が全面的に考慮されるので、高周波数でジュール損失が増加。 |
| 詳しい形状記述があるコイル導体 | 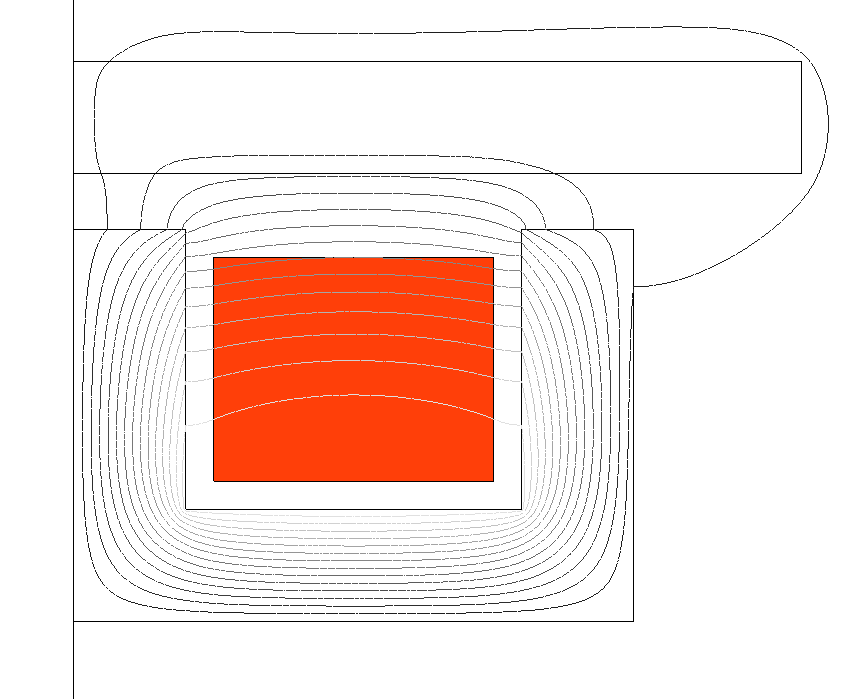 等価な均一電流密度分布を評価。 |
 粗いメッシュが可能。 |
 簡潔。必要なFE連成コンポーネントは1つのみ。 |
巻線の均質化によって表皮効果と近接効果を考慮。ソリッド導体領域の場合と同様に、高周波数でジュール損失が増加。 |
| 簡潔な形状記述があるコイル導体 | ジュール損失はゼロではなく、周波数によらず一定。結果は直流と低周波数による励磁でのみ正確。 |
|||
| 損失のないコイル導体 |
ジュール損失はゼロで、周波数によらず一定。 |
Fluxでメッシュ化コイル領域を使用する方法
前項では、Fluxのメッシュ化コイル領域の概念を理解するための基礎について説明しました。そこでは、この領域タイプによってモデル化した関連する物理現象と、この領域タイプから導いたサブタイプであるソリッド導体領域とコイル導体領域(詳細な形状記述がある領域、簡潔な形状記述がある領域、損失がない領域)の比較に重点を置きました。
メッシュ化コイル領域の各タイプをFluxプロジェクトで作成して使用する方法の詳細については、次の各トピックをご参照ください:
さらに、Fluxプロジェクトにおけるコイルの記述にある特定の内容の説明については、次の各トピックをご参照ください。このような内容として、対称性の利用、FE連成回路コンポーネントの作成、コイルモデルに対するFluxアプリケーションの影響などがあります:
参考文献
表皮効果と近接効果、コイルで発生する損失の評価、均質化手法を詳しく知ることができるように、こちらに参考文献の一覧を用意しています。