MV-7004：MotionSolveとMATLABを用いた倒立振子の制御

本チュートリアルでは、MotionViewとMotionSolveを使って倒立振子を安定化させる制御システムを設計する方法について学習します。

目標は、極配置法を使ったレギュレータを設計することです。倒立振子のMDLモデルファイルは用意されています。

チュートリアルには下記の手順が含まれます：

開ループシステムの安定性をチェック
MotionSolve線形解析を使って、線形化されたシステムのマトリックスA、B、CおよびDをエクスポート
MATLABを使ってコントローラを設計
MotionViewでコントローラをインプリメント
MotionSolve線形解析を使って、閉ループシステムの安定性をチェック
モデルに外乱力を追加し、MotionSolveでシミュレーションを実行

下の図はスライダー上の典型的な倒立振子です。システムは、自由度2を有し、4つの状態変数が存在します。垂直に立った振子の位置は不安定です。目標は、このコンフィギュレーションを安定させるレギュレータを設計することです。

目標を達成するためには、完全な状態のフィードバック制御法則を見つける必要があります。制御の入力は、全体X軸に沿ってスライダーにかかる力です。プラントの出力は、振子の全体Y軸周りの回転角度です。

mbd_modeling\motionsolveフォルダーにあるファイルinv_pendu.mdlをMotionViewに読み込んで開始します。モデルのトポロジーを見てみると、本演習に必要なものはすべて、モデルに含まれていることが分かります。ただし、実行するタスクによっては、特定のエンティティをアクティブまたは非アクティブにする必要があるかもしれません。

開ループモデルの安定性のチェック

固有値を計算し、倒立振子の釣り合い状態の安定性を確認します。

ProjectブラウザでForcesをクリックし、Control ForceOLがアクティブ、Control Force – CLとDisturbance-stepが非アクティブとなっていることを確認します。
General Actionsツールバーで、Run をクリックします。
Simulation typeドロップダウンメニューから、Static + Linearを選択します。
出力ファイル名をinv_pendu_ol_eig.xmlと指定します。
MDL animation file (.maf)オプションを選択します。
Runをクリックします。

ランが完了したら、ソルバー実行ウィンドウとメッセージログを閉じます。

MotionSolveにより計算された固有値は以下の一覧のとおりで、これはテキストエディタを使ってinv_pendu_ol_eig.eigファイルで確認することができます。

表 1. 開ループの固有値
Number	Real(HZ)	IMAG_FREQ(HZ)
1	-1.625311E-02	0.00000000E+00
2	-4.003403E-01	0.00000000E+00
3	5.582627E-01	0.00000000E+00
4	-1.733216E+00	0.00000000E+00

正の実数部を有する固有値が１つ存在し、現在のコンフィギュレーションではこのシステムは不安定であることを示しています。

Animateをクリックします。
結果のアニメーションH3Dファイルが隣のウィンドウに読み込まれます。
Resultsブラウザから個々のモードを選択します。

図 2.
Start/Pause Animation をクリックして、モード形状を表示します。

線形化されたモデルの取得

一般的に、制御システムの設計における最初のステップは、状態空間形式のシステムの線形モデルを得ることです。(1)

\begin{array}{l} \dot{x} = A x + B u \\ y = C x + D u \end{array}

ここで、 $A$ 、 $B$ 、 $C$ および $D$ は状態マトリックス、 $x$ は状態ベクトル、 $u$ は入力ベクトル、 $y$ は出力ベクトルです。A、B、CおよびDマトリックスは、状態、入力および出力選択に依存します。状態はMotionSolveによって自動的に選択され、選択された状態は、出力ファイルの1つにレポートされます。ここでは、入力と出力のみを定義する必要があります。

ProjectブラウザでSolver Variablesフォルダーを展開し、エンティティを確認します。
- Control Force Variable - CLは、制御法則が見つかった後、制御入力を定義するために使用されます。この時点では、これは無視します。
- Control Force Variable - OLは、Control Force - OLという名の力である制御プラント入力を定義するために使用されます。この力は、スライダーのボディにかかります。この変数は、ゼロに設定されています。これは、線形化されたシステムマトリックスを正しく生成するため、MotionSolveによって必要とされます。
- ソルバー変数Pendulum Rotation Angleは制御プラント出力を定義し、全体Y軸周りの振子の回転を計測します。
ProjectブラウザでSolver Arrayフォルダーを展開し、定義されているソルバー配列を確認します。
1. Plant-Iを選択します。この配列は、タイプPlant-Inputのソルバー配列エンティティを定義します。
2. Solver VariableがControl Force Variable - OLにセットされていることを確認し、OKをクリックします。
3. Plant-Oを選択します。この配列は、タイプPlant-Outputのソルバー配列エンティティを定義します。
4. Solver VariableがPendulum Rotation Angleにセットされていることを確認します。
  
  注: 線形化に使用されるプラント入力IDおよびプラント出力IDは、ソルバーデックのエクスポート中にMotionViewにより自動的に指定されます。
Runをクリックします。
Simulation typeドロップダウンメニューから、Linearを選択します。
出力ファイル名をinv_pendu_state_matrices.xmlと指定します。

図 3. MATLABマトリックスファイル出力を指定するSimulation SettingsダイアログのLinearタブ
Simulation Settings ダイアログ > Linearタブから、State-Space matrices (MATLAB)オプションを選択します。
MainタブでRunをクリックします。
基底名inv_pendu_state_matrices、拡張子.a、.b、.c、.d、.piおよび.poである6つの新しいファイルが得られます。.piおよび.poファイルには、入力および出力変数に関する情報が含まれています。
MotionSolveソルバーによって選択された状態に関する情報は：
- 全体Y軸周りの角変位
- 全体X軸に沿った並進変位
- 全体Y軸周りの角速度
- 質量マーカーの振子ボディ中央の全体X軸に沿った並進速度

MATLABでの制御システムの設計

制御システムの設計に関する詳しい解説は、本ドキュメントでは割愛します。しかし、倒立振子を安定させるための極配置（参考資料[1]参照）を使ったレギュレータ設計手順については、短く説明します。詳細は、制御の標準テキストおよびMATLABドキュメンテーションをご参照ください。

これは、システムが完全な状態制御可能（参考資料[1]および[2]参照）であるか、MATLABを使って簡単に検証できます。完全な状態のフィードバック制御法則 $u = - k * x$ を使用します。ここで、 $u$ は制御入力、 $k$ はゲインベクトル、 $x$ は状態ベクトルです。ここで、希望する極配置がベクトル $P$ に保管されることを前提とすると、極配置法を使って $k$ を計算することができます。[-20 –20 –20 –20] (rad/s)における希望の極について、MATLABでのAcker関数から下記が得られます： k=1e3[-2.4186 -0.0163 -0.070 -0.0033].

MotionViewでの制御力のインプリメント

制御力は単に、

u = - k * x

と表せます。モデルには、Control Force Variable - CLという名のソルバー変数が含まれます。これは、下記の式により定義されます：

`-1e3*(-2.4186*AY({b_pendu.cm.idstring})-0.0163*DX({b_pendu.cm.idstring}),-0.070*WY({b_pendu.cm.idstring})-0.0033*VX({b_pendu.cm.idstring}))`

これは単に、ゲインベクトル(k)および状態ベクトル(x)要素間のドット積です。このソルバー変数は、Control Force - CLという名の力を定義するために使用されます。

力Control Force - CLが非アクティブとなっている場合はアクティブにします。

閉ループシステムの安定性のチェック

SolverModeメニューからMotionSolveを選択します。力Control Force - CLが非アクティブとなっている場合はアクティブにします。
RunパネルのSimulation typeの下で、Linearを選択します。

出力ファイル名をinv_pendu_cl_eig.xmlと指定し、Run をクリックします。

固有値は下に示すとおり与えられます。

表 2. 閉ループの固有値
Number	Real(cycles/second)		Imag.(cycles/second)
1	-1.9595991E+00
2	-4.6976071E+00
3	-3.0372880E+00	+/-	1.3849641E+00

これらはすべて実数部が負で、システムは安定していることが分かります。負の実数部は、希望する極 (-20 rad/s = -3.038 Hz)に近い点にご注目ください。

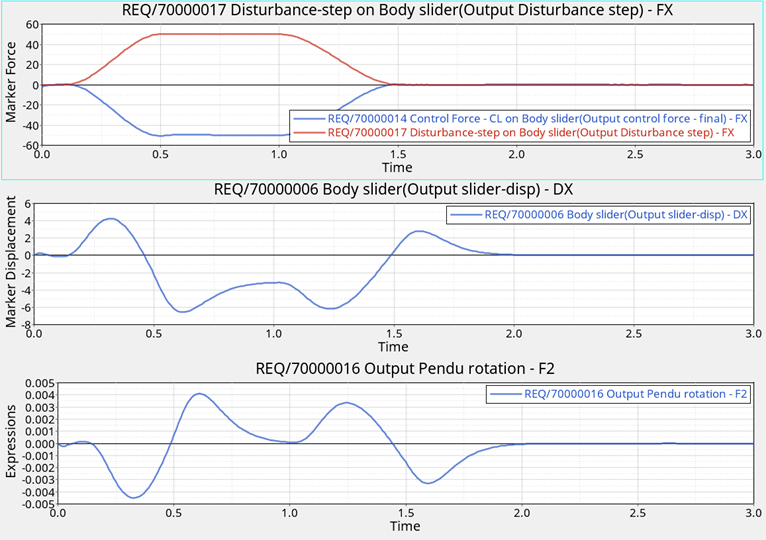
外乱力の追加とシミュレーションの実行

Disturbance-stepとタイトル付けされたスライダーにかかる力をアクティブにします：
```
Fx= `step(TIME,.1,0,.5,50) + step(TIME,1,0,1.5,-50)`
Fy=0
Fz=0
```
MotionSolveで動解析を実行するには、Projectブラウザで、非アクティブとなっている出力Output control force - finalおよびOutput Disturbance stepをアクティブにします。
ツールバーから、Run をクリックします。
Simulation typeドロップダウンメニューから、Transientを選択します。
出力ファイル名をinv_pendu_dyn.xmlと指定します。
End timeとPrint intervalをそれぞれ3.0と0.01に設定します。
MainタブでRunをクリックします。

ジョブが終了したらソルバーウィンドウを閉じ、inv_pendu_dyn.abfを使って新しいHyperGraphページに以下の結果をプロットします。

Output	Y-Type	Y-Request	Y-Component
制御力	Marker Force	REQ/70000014 Control Force - CL on Body slider(Output control force - final)	FX
外乱力	Marker Force	REQ/70000017 Disturbance-step on Body slider(Output Disturbance step)	FX
スライダー変位 -X	Marker Displacement	REQ/70000006 Body slider(Output slider-disp)	DX
振子の角変位	Expressions	REQ/70000016 Output Pendu rotation	F2

外乱力、制御力、スライダーのx変位、振子の角変位のプロットを下に示します。

参考資料

Feedback Control of Dynamic Systems, G. G. Franklin, J. D. Powell, and A. Emami-Naeini, Third Edition, Addison Wesley.