タンクテスト出力からのデータを使用することにより、Radiossへの入力として使用できる、供給されるガスの温度とマスフローを得ることができます。
タンクテストで、インジェクションの点とタンク中央の点で圧力の計測が可能で、それらが等しければ、圧力変化を得ることができます。また、供給されるガスの量と、テストでのガスの特性も得られます。
温度については、温度計の精度が十分でないことが多いため、正確なテストデータを取得することがより困難です。そのため、タンクテストの温度が間違っている可能性があります。
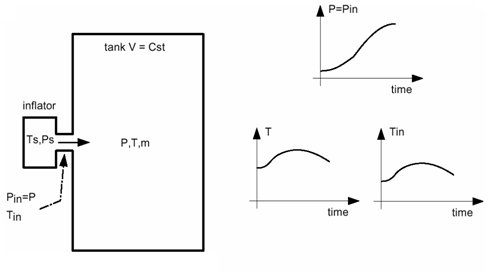
図 1. 未知の質量流量
以下は、注入温度とタンク内の温度が既知の場合と未知の場合があることを考慮に入れたケースになります。
インジェクターとタンクの温度が未知のケースでは:
- 初期と注入ガス組成
それぞれの要素のモル質量(
) とモル分率 (
)が既知であればガスのモル質量(
)を定義することが可能です:
(1)
ガスの混合体の単位体積当たりの平均熱容量はAmagat-Leduc方程式で与えられます:
(2)
前の式を用いて、初期状態と注入された混合体の熱容量係数(
)の定義が可能な場合があります。
注入されたガスの特性が既知であれば、初期のガスと混合体のマスフローとインジェクターの温度を見つける事が可能です。以下の基礎方程式が解析の実行に用いられます。
- 理想気体の状態方程式は:(3)
ここで、
- 断熱の方程式は:(4)
ここで、
は系の全エンタルピー(インフレーター+タンク)です。
エネルギー保存から、タンクテストの基礎のエネルギー方程式は次のように書くことができます:
(5)
ここで、タンクテストは断熱的であるため、
=0となります。タンクテストの一定体積は、
=0を意味します。
したがって、
式 5は下記のように要約することができます:
(6)
インフレーター温度
式 6で、未知の変数は
のみです。
他の変数は既知であるか、または
式 2と
式 3を用いて決めることができます:
-
および
- i = a~cの場合:
は、式 2を使用して計算されます。および
-
したがって、式 6で、注入されるガスのインジェクタ
における温度は、
の反復で見つけることができます。最初に温度を推定し、収束解を得るのに6回の反復もあれば十分です。
マスフロー
タンクテストの上部での圧力の時間変化が既知であれば、マスフロー比率は次の式で決める事ができます:
(7)
ここで、
-
- 実験の間の全圧力変化
-
- 全注入質量
式 7 は、質量変化と圧力変化の関係が完全に増加関数の場合に成り立ちますが、これはその場合です。
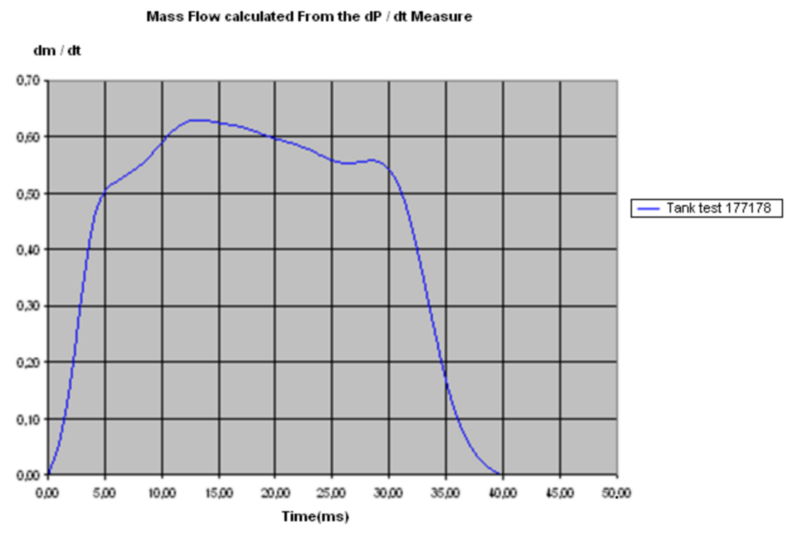
図 2. マスフロー曲線 - マスフローの時間変化
インフレーターガス速度
圧力はすぐに一様になるので、式は次のように記述できます。
、
密度が分かれば、
と
の関数として表現することができます:
(8)
さらに、
、ガス内の音速は:
(9)
また、
の場合、
となり、速度は音速となります。
- インジェクタの温度が既知の場合:
- タンク内の温度が既知の場合:
または
- タンク内の温度が一定の場合:

