定式の選択

ALE（Arbitrary Lagrangian-Eulerian）表現はその後、上の古典的な運動表現の利点を組み合わせ、それぞれの欠点をできる限り最小にするために開発されました。

Euler定式化

Eulerian定式化は流体力学において古典的な表現です。メッシュは固定され、材料がメッシュの中を流れます。方程式は対流項を考慮するため、Lagrange定式化に関して修正されます。

これは材料データでのフラグにより、特定のパートに対してアクティブ化されます。

/EULER/MAT/mat_ID

Euler定式化の要素では移動境界はインターフェースの取り扱いは困難です。Euler定式化は領域移動の境界のある多くのケースでは使うことができません。

Lagrange定式化

Lagrange定式化は構造解析において古典的な表現です。メッシュは材料の点に固定され、材料の変形に従います。材料（構造）とメッシュの間の滑りは許されません。荷重と境界条件は容易に材料の点（節点）に与えることができます。

Lagrange表現では自由表面と異なる材料間のインターフェースを容易に追跡することができます。しかしながら、構造がひどくゆがんだ時、Lagrange定式化の要素も材料の変形に従うため同様にゆがみます。したがってこれらの場合、Lagrangianシミュレーションの精度とロバスト性は大幅に低下します。

これがRadiossでのデフォルト定式化で、材料がEuler（/EULER/MAT/mat_ID option）としても、ALE（/ALE/mat_ID option）としても定義されていない場合、材料はLagrangeです。

ALE定式化

ALEは、Arbitrary Lagrangian-Eulerian定式化を表しています。材料は任意に移動するメッシュの中を流れます。材料とメッシュの両方が実験的に移動します。LagrangeとEuler定式化の組み合わせの様に見ることができます。

この定式化は、材料データでのフラグにより、特定のパートに対してRadioss内でアクティブ化されます：

/ALE/MAT/mat_ID

ここで、

mat_ID

ALE定式化がセットされる材料のID

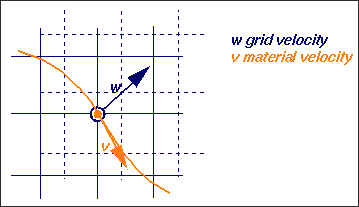
図 1. 任意のグリッド速度と変位

実際、ビルトインのアルゴリズムでALE領域境界の変位に基づいてスムーズなグリッド変形が決められます。いくつかのアルゴリズムが利用可能です（DONEA、SPRINGS、DISP、ZERO）。

ALE定式化はLagrangian（w=u：グリッド速度が材料速度と等しい）、またはEulerian（w=0： グリッド速度が0に設定される）で縮退させることができます。

図 2. Euler、LagrangeとALEメッシュ

ALEとLagrange材料の間の境界節点はLagrange（グリッド速度と材料速度が等しい）に設定される必要があります。ALEとEuler材料の間の境界節点ではグリッド速度を0に設定する必要があります。