手法

このセクションの目的は、正しいRadioss ALE/CFDモデルを生成するためのいくつかの手順を示すことにあります。

CADクリーニング

通常、構築するモデルに対応するCADモデルを受け取ることになります。最初のタスクは、このCADモデルをクリーンにして単純化することです：
  • 自動テトラメッシュを用いてサーフェスを追加して閉じたボリュームにする
  • メッシュの引き延ばしを制御してサーフェスを追加する
  • パッチサーフェスでメッシュゾーンを準備する
    • 解くことが可能なサイズよりも小さい詳細部分を削除する
    • サーフェス上の線の拘束を可能な限り除去する

メッシュ生成

ヘキサ要素（または2次元解析では四角形要素）のみがALEまたはEuler定式化には適合します。メッシュ生成において、通常のテクニックはそれぞれの考慮する領域においてメッシングの最初に三角形の外表面を作成し、次に内部ボリュームに対しをテトラメッシュを自動生成し、最後にそのテトラ要素をそれぞれ４つのヘキサ要素に分割することです （要素数を注意深く監視します）。三角形メッシュサイズはテトラ要素のために、計画したメッシュサイズの3.5倍より大きくするべきです。


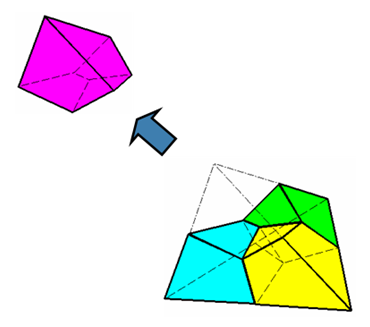
図 1. テトラのヘキサメッシュへの変換
このリメッシュ機能は、HyperWorksの"split"の中にあります。テトラ要素を6面体要素にリメッシュするには、split into hexasを選択します。


図 2.
必要な場合にはいくつかの引き延ばしを追加します、例えば：
  • 流出
  • 流入
  • サイレント境界（NRF）
  • チューブ

もちろん、ヘキサ要素が生成できる場合には、他のテクニックも使うことができます。

境界層のためには、壁要素のサイズが壁要素サイズで説明されたように決められます。境界層のためのメッシュは一般的に、壁表面を三角形でメッシングすることにより得られます。次にサーフェスメッシュの引き延ばしを用いて、ソリッドの五角形のメッシュを生成します。五角形要素は、図 3に示すように後でヘキサ要素に簡単に分割できます。


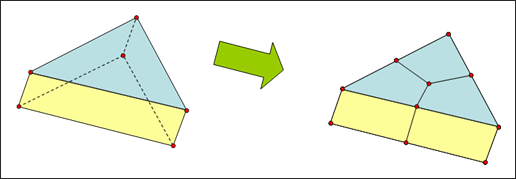
図 3. 五角形要素の3つのヘキサ要素への分割

メッシュ特性の定義

メッシュサイズを考慮する際には2つの点に留意します：
  • 速度および圧力勾配： 乱流壁付近の要素サイズはy+値に支配され、これは100から1000またはそれ以上の範囲にすることができます（パイプ内ではy+値が8000ぐらいで正確な結果が得られます）。その領域から、粗い領域への漸変が一般的に用いられます。
  • 音の精度： 最大要素サイズが、着目する最小波長から得られます。一般的に波長あたり12要素の使用が許容できます。

明らかに最初の条件は障害物や壁に近い領域を支配し、2番目は全計算領域の最大サイズを拘束します。

メッシュの構築には通常、いくつかのトレードオフがに必要になります。シミュレートされる全時間 T t o t MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8 qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9 q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake aacaWGubGaamiDaiaad+gacaWG0baaaa@3C96@ は次のように評価できます：

T t o t ∼ 20 ⋅ L / c MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamivaiaads hacaWGVbGaamiDaiablYJi6iaaikdacaaIWaGaeyyXICTaamitaiaa c+cacaWGJbaaaa@410A@

ここで、
L MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamitaaaa@36C7@
最大モデルサイズ
必要な全CPU時間が、計算可能性と精度のトレードオフを確立する主要な基準となり、これは次のように見積もることができます：
  • CPU = Ttot/dtc * Number of element * cpu/el/cycle

望ましいシミュレーションを実行するためのメッシュ生成は、2つの基準と計算可能性（可能なCPU 時間）と精度により注意深く決められる必要があります：

基準1： 移流

  • 解く必要のある渦あたり最小10要素
  • 局所Strouhal数が音源領域の」着目する"周波数範囲の1/6を超えないこと

    Str = f h/v < 1/6

    例： fmax =600 Hz, v=30m/s ≥ h ~ 8 mm

基準2：音響伝播

  • 音源から離れた領域で必須
  • 伝播方向に沿って波長当たり6要素

    例： fmax = 600 Hz, c=300 m/s ≥ h ~ 8cm

トレードオフ

利用可能なCPUの中でのシミュレーションの全時間と限界時間ステップでは、時間ステップはCourantの安定条件を満足するように自動的に設定されます：
  • dt = Min (h) / c
全計算時間はモデル中にある最小要素の周波数の倍数となります。全CPU時間はサイクル数（終了時間を時間ステップで割ったもの）、要素数、およびそれぞれの要素当たりの計算コスト（計算機に依存）に比例します：
  • T = Ncycle * Nelem * Cost / cycle / elem

実際には、シミュレーションのサイクル当たりのコストを知るために、大きなシミュレーションを開始する前に数サイクルの実行を行うことが推奨されます（初期化の時間を差し引くことを忘れないでください）。

障害物回りの空気の流れ（下の図）が検討され、シミュレーションの目的がメッシュのいろいろな位置の流れによって生成される騒音を測ることである場合を考えます。そのメッシュは少なくとも4つの異なる領域からなる必要があります （メッシュ生成）：
  • 粗いメッシュ（障害物のすぐ周りを除いた全計算領域）
  • 再分化されたメッシュ（障害物近傍）
  • 流入要素（1列の要素）
  • 流出要素（1列の要素）
流れの中の障害物の特性長さlで、一般的に3つのメッシュゾーンに分かれます：
ゾーン 典型的な要素サイズ 註：
非常に細かい a 障害物のように選択されたものはそれぞれの方向で最小20セルで離散化
細かい 2aから3a  
粗い 4aから6a 粗いセルが、着目する最大周波数の対流の近似であることを確認してください。
問題で着目する最高周波数がfの場合、下記より大きいセルがメッシュ内にあってはいけません：
  • Size of element < C / 10.f
ここで、
C
流体中の音速
流入と流出要素の厚さは、計算領域の隣接要素の1/10であるべきです。


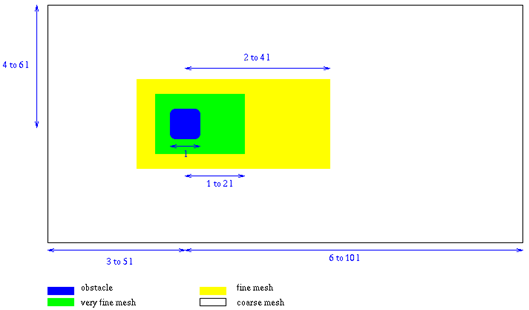
図 4. CAA問題のための典型的なメッシュでの要素数（特定の適用対象では変化します）

低Mach数の問題（0.2より小さい）では、満足な結果は準-圧縮性の仮定の下で得ることができます。これは計算時間の節約になります。圧縮性は、Navier-Stokes方程式が波動方程式を含むことを示しています。そのため、音と流体流れを同時に取り扱うことが可能で、高い数値精度を得ることができます。準-圧縮性は、輸送の項が運動量方程式を除いて無視されることを意味します。したがって、流体材料則の中のC1を減らすことにより、音速が減少して時間ステップが増加します（例えば、C1の値を10分の1にすることにより、時間ステップは約３倍になります）。