スポット溶接(ボルトまたは接着結合)
- 節点結合
- スプリング(/PROP/TYPE13)結合
- ソリッド結合
スプリング(/PROP/TYPE13)結合とソリッド結合は、ボルトまたは接着結合をモデル化することもできます。
節点結合
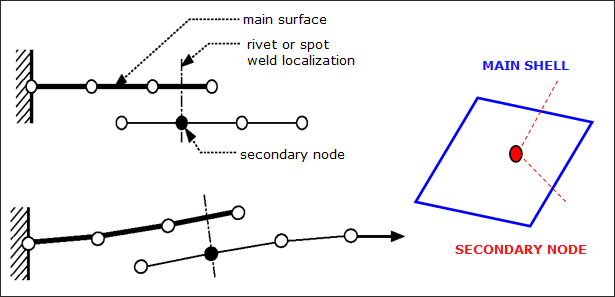
図 1. 2つのシェルサーフェス間の結合の例
スプリング(/PROP/TYPE13)結合
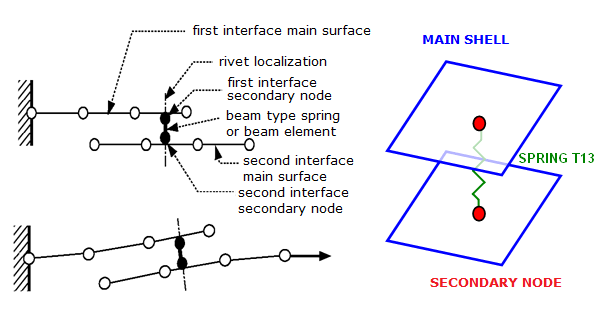
図 2. スポット溶接のモデリング
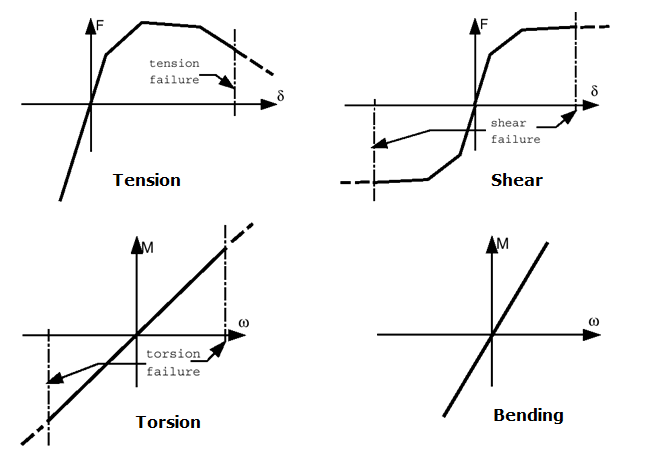
図 3. スプリングタイプ13 - スポット溶接のための典型的な入力
- スプリングタイプ13で使用可能な破壊基準を使用。詳細については、/PROP/TYPE13 (SPR_BEAM)の破壊基準のコメントを参照のこと。
- タイドコンタクト(タイド接触(/INTER/TYPE2))のSpotflag= 20、21または22を使用。注: スポット溶接のためのスプリングTYPE13を使ったモデル化テクニックは、溶接線、ヘム、接着、ボルトといった他の種類の結合にも用いることができます。ボルトのモデル化ではタイドインターフェースの利用は必要ではなく、シェルの節点を直接剛体に入れて結合することができます。
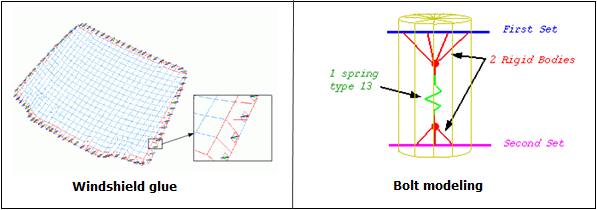
図 4. 接着とボルトのモデル化の例
- : 付加質量
-
- セカンダリ節点の質量
- セカンダリ節点とその中心の距離
- セカンダリ節点の慣性
Spotflag=0の場合、セカンダリ節点の慣性がメイン節点に伝達されるため、付加質量は有りません。付加された慣性が大きすぎると精度の深刻な低下を招きます。
ソリッドスポット溶接
8節点の3次元ソリッド要素(/PROP/TYPE43を使用)と/MAT/LAW59+/FAIL/CONNECT(または/MAT/LAW83+/FAIL/SNCONNECT)を使用して、ソリッドスポット溶接をモデリングすると、より正確な結果が得られる場合があります。
ソリッド要素とプロパティ
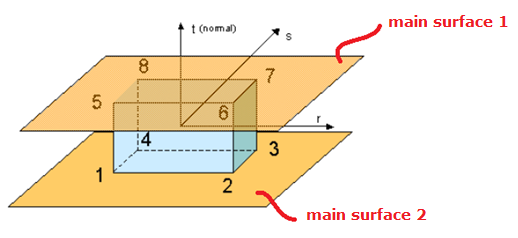
図 5.
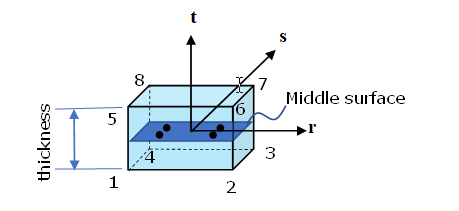
図 6.
シェルシートへの結合
INTER/TYPE2は、ソリッドスポット溶接と上下2つのメインサーフェスを結合するために使用できます。1つのシェルに結合された平面(1、2、3、4)の節点と、もう1つのシェルに結合された平面(5、6、7、8)の節点です。シェルに結合された他の平面(平面(1、4、8、5)など)を設けることは許可されません。
材料と破壊モデル
- せん断試験(荷重とスポット溶接上部サーフェスの角度は0度です)
- 法線引張試験(90度試験)
- せん断と法線の組み合わせ試験(30度試験、45度試験、90度試験など)
- モーメント試験(剥離試験)
ヤング率
スポット溶接の剛性は、試験ごとに異なります。法線試験では、上下のシートが変形するため、これはせん断試験の場合より小さくなります。したがって、測定される剛性は通常、せん断試験の真応力と変位の曲線から得られます。
/MAT/LAW59+/FAIL/CONNECT
- 材料降伏曲線:LAW59では、法線方向とせん断方向のスポット溶接材料降伏曲線が要求されます。法線方向の降伏曲線(Y_fct_IDN)は、法線引張試験(90度試験)によって特定でき、せん断方向の降伏曲線(Y_fct_IDT)は、せん断試験(0度試験)によって特定できます。
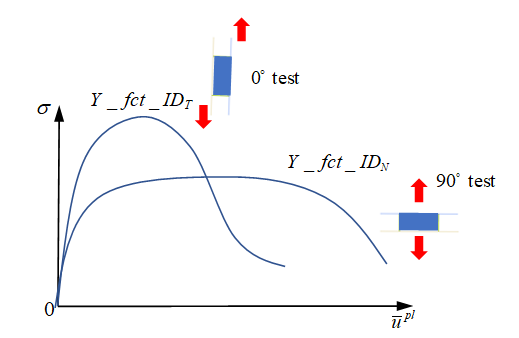
図 7.この場合、最大応力も曲線内に表されます。入力降伏曲線の参照変位速度が与えられた場合、Radiossでは、この参照変位速度に関して変位速度効果が考慮されます。
- スポット溶接破壊:ソリッドスポット溶接の損傷と破壊は、/FAIL/CONNECTで考慮できます。変位基準やエネルギー基準を使用してスポット溶接の破壊を表すことができます。
- 変位基準の場合、次の2つの代替挙動タイプにより法線変位またはせん断変位に達すると、破壊が生じます:
- 非連成破壊(Ifail=0: 一方向破壊)
(2) ここで、法線方向については = 33、接線方向については = 13または23です。
法線引張試験(90度試験)では、ユーザー定義の最大変位に達すると、要素が破断します。
せん断引張試験(0度試験)では、ユーザー定義の最大変位に達すると、要素が破断します。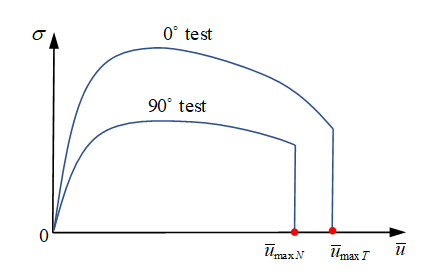
図 8.モード組み合わせ試験(30度試験や60度試験など)では、ソリッドスポット溶接の破壊では、せん断と法線の組み合わせ応力の効果は考慮されません。各方向の破壊は別々に考慮されます。これら2つの応力のどちらかが対応する最大変位に達すると、要素が破断します。組み合わせ応力を考慮するには、代わりにIfail=1と設定すると考慮されるようになります。
- 連成破壊(Ifail=1: 多方向破壊)
(3) Ifail=1の場合、モード組み合わせ試験では、最大応力やに達する前に要素が破断します(現実により近い)。曲線破壊サーフェスを表すには、パラメータをフィッティングするために、少なくとも4種類の組み合わせ試験が必要です。
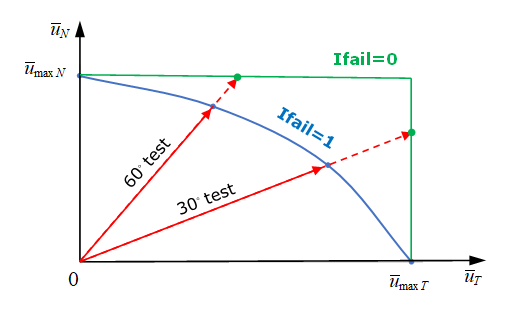
図 9. 破壊サーフェス
- 非連成破壊(Ifail=0: 一方向破壊)
- エネルギー基準の場合、最大内部エネルギーに応じて、法線方向またはせん断方向の内部エネルギーに達すると、破壊が生じます。
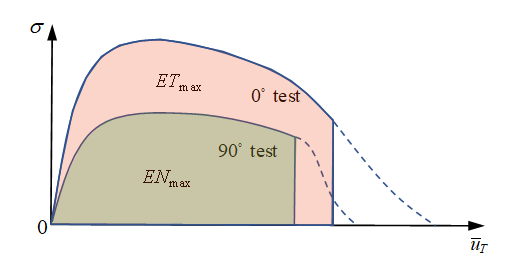
図 10.モード組み合わせ試験では、内部エネルギーに対する多方向の影響に関する要素の破壊も考慮されます。法線方向とせん断方向の内部エネルギーが入力された場合、次の条件が満たされると、要素は破断します:(4) 内部エネルギーの合計のみを入力する場合、次の条件が満たされると、要素は破断します:(5) との両方が入力された場合、これら2つの基準のどちらかに先に達した時点で、要素が破断します。
変位基準とエネルギー基準の両方を定義できます。どちらかの基準に先に達した時点で、要素が破断します。要素が削除されるのは、1つの積分点が破壊基準に達したとき(Isolid=1の場合)、またはすべての積分点が破壊基準に達したとき(Isolid=2の場合)です。
- 変位基準の場合、次の2つの代替挙動タイプにより法線変位またはせん断変位に達すると、破壊が生じます:
- スポット溶接の軟化:破壊基準(変位基準またはエネルギー基準)に達した後、応力は一気に0に低減されるか、パラメータとを使用して次の式で徐々に減少させることができます:
(6) 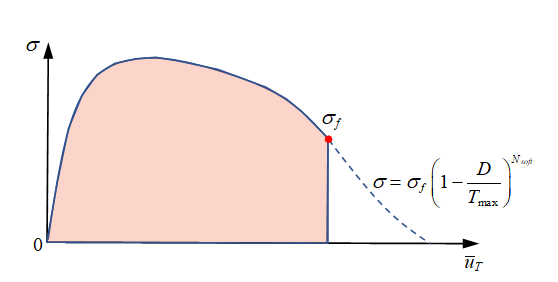
図 11.図 12 は、さまざまなおよびで、応力低下の挙動がどのように影響を受けるのかを示しています。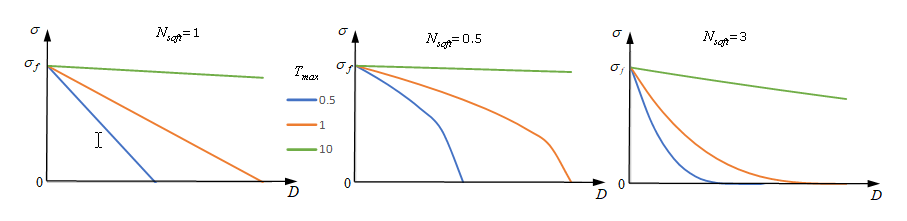
図 12.
/MAT/LAW83+/FAIL/SNCONNECT
- 材料降伏曲線:LAW83では、fct_ID1を使用してスポット溶接材料曲線を入力できます。LAW59の入力では、法線方向とせん断方向の2つの降伏曲線が必要であるのに対して、LAW83では1つの曲線のみが使用されます。この曲線では、せん断試験から降伏曲線を取得する必要があります。さらに、LAW83の降伏曲線fct_ID1は、真応力と塑性変位の関係として定義されていませんが(LAW59ではこのように定義されています)、正規化された応力と塑性変位の曲線である必要があります。LAW83では、降伏応力は、パラメータとして入力される最大応力で正規化されます。
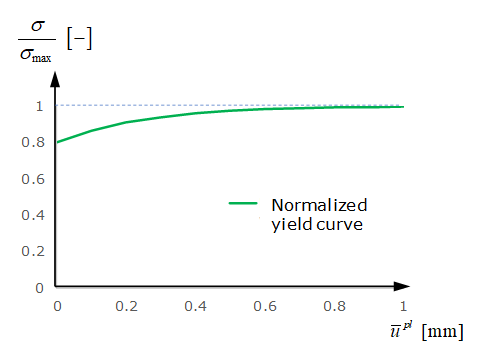
図 13.スポット溶接の法線応力とせん断応力のさまざまな組み合わせにより、降伏曲線は異なります。これは、LAW83ではパラメータを使用して表現できます(これはLAW59では考慮されません)。LAW83で正規化された降伏応力は次のとおりです:(7) モーメントの影響が考慮されない場合、LAW83で正規化された降伏応力は次のとおりです:(8) 図 14 は、組み合わせ試験における正規化された最大応力が、LAW83とLAW59でどのように違うのかを示しています。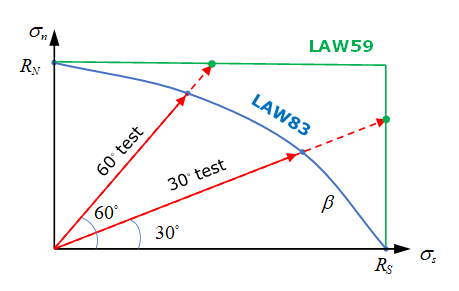
図 14.図 15 は、値の違いに応じて、LAW83を使用した組み合わせ試験で正規化された最大応力がどのように変化するのかを示しています。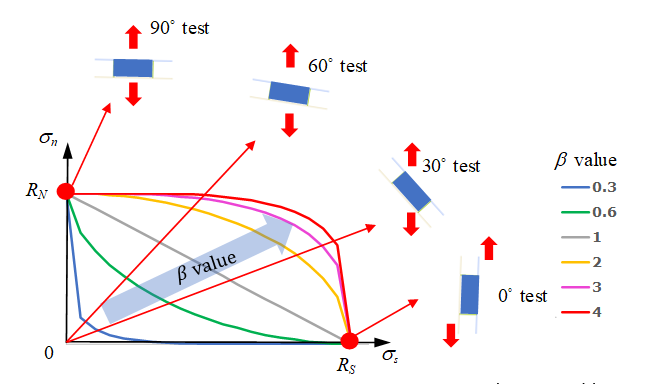
図 15.パラメータを使用して、スポット溶接でのモーメントの影響を表します。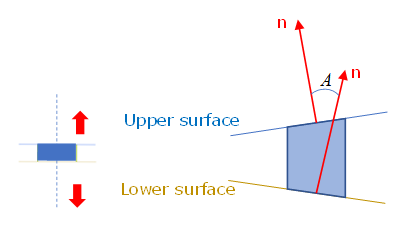
図 16. 非中心引張試験(剥離試験)を使用して、剥離試験の最大応力を低減させます。 は、スポット溶接の上下サーフェス間の角度の正弦です。この値は、スポット溶接の変形時に、[-1,1]という範囲内で変化します。パラメータは、実際の実験データに一致させるためにシンプルなFEMモデルを使用してフィッティングできます。 1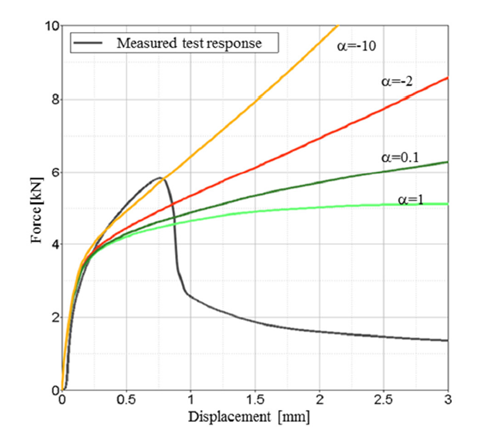
図 17. 剥離試験で値の違いが力と変位の関係に及ぼす影響曲線入力fct_IDNおよびfct_IDSを使用して、変位速度が材料の降伏曲線に及ぼす影響を考慮することもできます。
- 材料の損傷と破壊:スポット溶接破壊には、/FAIL/SNCONNECTを使用できます。この破壊モデルでは、損傷開始と破壊の塑性変位(法線方向とせん断方向)が必要です。
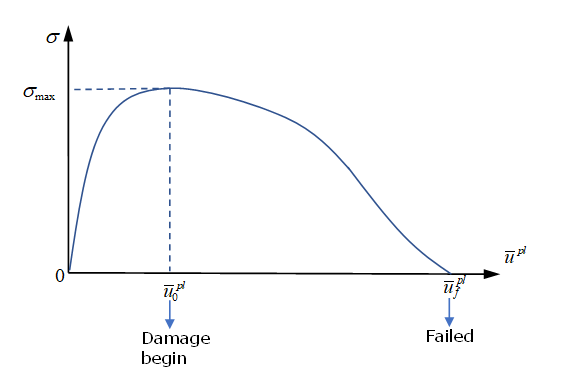
図 18.モード組み合わせ試験では、LAW83での最大応力と同様に、損傷開始時の塑性変位を表すと、破壊時の塑性変位を表すが必要です。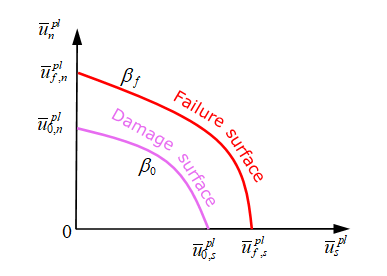
図 19.モーメントを伴うスポット溶接(剥離試験)では、LAW83での最大応力と同様に、剥離試験の損傷開始時の塑性変位を表すと、剥離試験の破壊時の塑性変位を表すが必要です。表 1. 2つのスポット溶接モデリング手法の一般的な機能 /MAT/LAW59+/FAIL/CONNECT /MAT/LAW83+/FAIL/SNCONNECT 降伏曲線 2つの降伏曲線(法線方向とせん断方向) 最大応力を含む1つの正規化された降伏曲線 モード組み合わせ試験での最大応力 組み合わせ試験での法線とせん断の効果は考慮されません。 を使用して、モード組み合わせ試験での法線とせん断の影響を考慮します。 破壊 破壊基準 変位基準 1方向破壊 多方向破壊
変位基準、 多方向破壊
エネルギー基準 1方向破壊 多方向破壊
モード組み合わせ試験での破壊 変位基準のとエネルギー基準のを使用して比例的に制御されます。 以下により制御 モーメントの影響 (剥離試験)
入力での制御なし 以下により制御 軟化 を使用(応力曲線は下降) 損傷変位と破壊変位に関連(応力は線形減少)