Cohesive Zone Modeling
Cohesive zone modeling can be used to model adhesive and bonded interfaces and corresponding crack initiation and propagation.

Figure 1.
There are multiple methods/techniques by which interfaces can currently be modeled in OptiStruct. In the damage-based method that relies on cohesive elements, thickness of the adhesive/bonded interface can be considered. For other methods/techniques, thickness effect is excluded. The term technique is used to distinguish between the element types that are used, which are cohesive elements and contact elements.
Interface Implementation Methods
Cohesive zones are used to model adhesive/bonded interfaces, where layers/parts are connected with resin or adhesive.
- Potential-based method
- Damage-based method
There are three modes for the cohesive zone deformation.
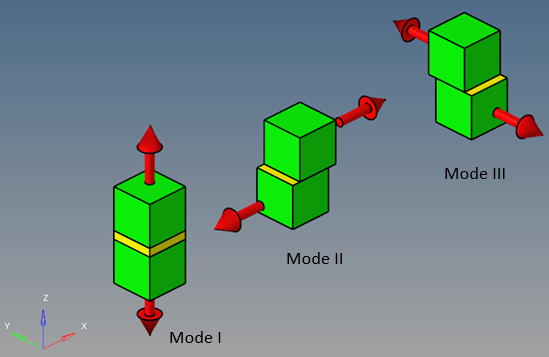
Figure 2.
The system x-y-z in Figure 2 is the cohesive zone coordinate system. Unless it is specified in the PCOHE card, the establishment is shown in CIFHEX/CIFPEN Bulk Data Enty. Mode I is the normal opening in z-direction, Mode II and III are the shear opening in x-z plane and y-z plane, respectively.
In contact, it is assumed that contact pairs have the same property in two tangential directions. Therefore, it is suggeted that the cohesive property in Mode II and III be the same.
Potential-based method (MCOHE)
In the potential-based method the traction-opening model is selected between three types of curves.
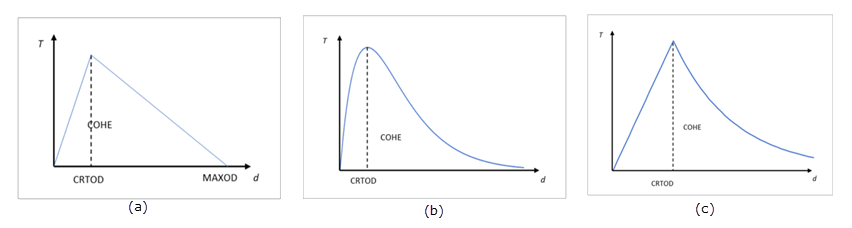
Figure 3. a) Biliniear; b) Exponential; c) Linear-Exponential
In the potential-based method, only a single layer of cohesive elements is allowed for modeling a particular adhesive or bonded interface.
Typically, tensile and shear deformations at the interface are of interest to determine the integrity and/or degradation of the adhesion/bonding. Stiffness in compression is controlled via the SFC field on the MCOHE entry.
- The opening in Mode I, II and III.
- The mixing coefficient, which can be input on the BETA field.
- Bilinear:
(2) - Exponential:
(3) - Linear-exponential:
(4)
- is the CRTOD
- is the MAXOD
- is the combined relative displacement ()
Also, in the linear-exponential curve definition, one more parameter, , is required, which is input in the field EXP in MCOHE card.
Damage-based Method (MCOHED)
Damage-based method allows modeling of finite thickness of adhesive/bonded interfaces. This allows for modeling adhesive layers based on experimental data.
In this method, crack growth is controlled by development of damage in each element. The damage of an element is controlled by two indices, namely, damage initiation index and damage evolution index. In each element, the two indices are initially zero. With loading, damage initiation index is increasing. When damage initiation index reaches 1.0, damage appears. Damage initiation index keeps being 1.0 afterwards and damage evolution index starts to increase. When damage evolution index reaches 1.0, the damage is matured and there is no cohesion afterwards. Thus, crack advances.
The damage initiation and evolution are controlled by several parameters defined in MCOHED, DMGINI (Damage Initiation) and DMGEVO (Damage Evolution) cards by users.
Depending on the modeling technique (element-based versus contact-based), either CIFHEX/CIFPEN/PCOHE entries or CONTACT interfaces are required. Refer to Modeling Techniques.
Elasticity modulus/Penalty stiffness in the three directions are defined on the KI, KII, and KIII fields of the MCOHED entry, in which KI is for the normal direction, KII and KIII are for the two tangential directions. Single or multiple layers of cohesive elements can be defined in the interface.
Typically, tensile and shear deformations at the interface are of interest to determine the integrity and/or degradation of the adhesion/bonding. Stiffness in compression is controlled via the SFC field on MCOHED entry in the element-based technique. When contact-based technique is used, stiffness in compression is determined by contact property.
For the element-based technique, thickness of the cohesive element layer can be defined using the THICKNESS field on PCOHE. For contact-based technique, thickness of the cohesive zone is considered internally to be one unit.
The following introduction on damage-based cohesive model is for element-based technique. They are also valid for contact-based technique, if thickness is replaced by unity.
The DMGINID and DMGEVOID fields on MCOHED are used to specify the mandatory DMGINI and DMGEVO Bulk Data Entries in element-based modeling. When contact based modeling is used, stiffness in compression is determined by contact property.
The relative displacement between the nodes of the top and bottom faces are calculated similar to the potential-based method. First, the trial traction values (/) are calculated by multiplying the penalty stiffness (which is elasticity modulus divided by thickness in quantity) and the opening in the three modes.
Next, determination of the damage initiation is carried out, using the specified criteria on the CRI field of the DMGINI entry.
Strain-based Initiation Criteria
- The maximum strain value is defined on the V1, V2, V3 fields of the DMGINI entry.
- The actual strain is calculated by the formula: (relative displacement divided
by the thickness)
Where, thickness is defined by the THICKNESS field on PCOHE.
- Using both maximum strain and actual strain, the damage initiation determination
is done based on the following formula:
- MAXE
-
(5) Where,- = V1.
- = V2.
- = V3.
- QUADE
-
(6) Where,- = V1.
- = V2.
- = V3.
Stress-based Initiation Criteria
- The maximum stress value is defined on the V1, V2, V3 fields of the DMGINI entry.
- The actual stress is the value of trial traction in each of the corresponding three directions.
- Using both maximum stress and actual stress, the damage initiation
determination is done based on the following formula:
- MAXS
-
(8) Where,- = V1.
- = V2.
- = V3.
- QUADS
-
(10) Where,- = V1.
- = V2.
- = V3.
If damage initiation criteria are not satisfied, then there is no damage. The trial traction is equal to actual traction. Therefore, there is no crack initiation and propagation, and the corresponding cohesive-related output are printed to the result files.
- Displacement-based damage evolution index (TYPE=COHDISP on DMGEVO entry)
- Energy dissipation-based damage evolution index (TYPE=COHENRG on DMGEVO entry)
For either type of damage evoluation index calculation, either linear (SHAPE=LIN) or exponential (SHAPE=EXP), shapes of the traction-opening curve can be used on the DMGEVO entry.
is the damage evolution index (it is always ≤ 1.0) and in the output it is referred as damage index.
Displacement-based Damage Evolution Index
If SHAPE = LIN:
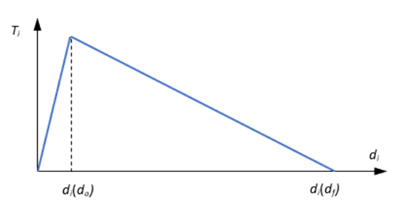
Figure 4.
If SHAPE=EXP
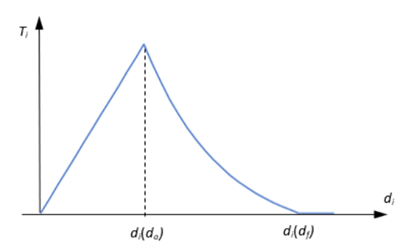
Figure 5.
- Maximum opening () in history. If the cohesive zone is only being loaded, then is equal to the current , which is calculated by OptiStruct and updated at each step. If cohesive zone is also unloaded, then within the unloading zone, is equal to the maximum in history (as it could be a previous value of , prior to the beginning of unloading).
- Critical opening (the opening, , when damage is initiated – when the crack initiation criteria are satisfied).
- Maximum opening ().
- W1 field on the DMGEVO entry.
- ALPHA field on DMGEVO entry.
- Current opening at each step of the solution.
Energy Dissipation-based Damage Evolution Index
For energy dissipation-based damage evoluation index, the critical total energy ( ) also known as fracture toughness is the key value used for calculations. Its calculation and usage depend on the type of the curve (LIN/EXP) and the mode mix method (MMXFM = blank, 1,2). represents the energy at which failure occurs.
W1, W2, and W3 fields on the DMGEVO entry define the critical energies in each of the three fracture modes.
- Normal Fracture Mode I:
- W1 = (Power law) = (Benzeggah-Kenane (BK) form) defines the critical energy at which failure occurs in normal direction.
- Shear Fracture Mode II:
- W2 = (Power law) defines the critical energy at which failure occurs in Mode II.
- Shear Fracture Mode III:
- W3 = (Power law) defines the critical energy at which failure occurs in Mode III.
is the total energy (area under the curve) until the current solution step.
If SHAPE = LIN:
- The maximum opening () in history. If the cohesive zone is only being loaded, then is equal to the current , which is calculated by OptiStruct and updated at each step. If cohesive zone is also unloaded, then within the unloading zone, is equal to the maximum in history (as it could be a previous value of , prior to the beginning of unloading).
- The critical opening (the opening, , when damage is initiated – when the crack initiation criteria are satisfied).
- The opening at which zero traction is produced in the analysis.
- Effective traction when crack initiation criteria are satisfied.
- If MMXFM field is blank:
(16) - If MMXFM field is set to 1 (Power law): The is derived from:
(17) Where, , , and are the W1, W2, and W3 fields on the DMGEVO entry.The value of is derived as:(18) Where, is the ALPHA field on DMGEVO entry.
- If MMXFM field is set to 2 (BK form):The value of is based on the following equation:
(19) Where,- ALPHA field on DMGEVO entry.
- and
- W1 and W2 fields on the DMGEVO entry.
is the total energy (area under the curve) until the current solution step.
If SHAPE=EXP:
- Compound traction.
- Elastic energy absorbed by the cohesion. It is the area under the straight line-section (before damage initiation) of the exponential curve.
- Critical opening (the opening, , when damage is initiated – when the crack initiation criteria are satisfied).
- Final opening.
- Total energy that can be dissipated by cohesion under the current opening pattern (combination of , , and ). The critical energy, , is calculated automatically by OptiStruct and it depends on the mode mix form (MMXFM field on DMGEVO entry) and the energy that can be dissipated in each mode (W1, W2, and W3).
- If MMXFM field is blank:
(21) - If MMXFM field is set to 1 (Power law):The is derived from:
(22) Where,- , , and
- The W1, W2, and W3 fields on the DMGEVO entry.
- , , and
- The energies under the traction-opening curve until the current step. They depend on the type of curve (LIN/EXP).
However, by default, for the exponential curve, the same value of is used for the linear curve.(23) - If MMXFM field is set to 2 (BK form):The value of is:
(24) Where,- ALPHA field on DMGEVO entry.
- and
- W1 and W2 fields on the DMGEVO entry.
is the total energy (area under the curve) until the current solution step.
Calculating Actual Traction
Actual traction is calculated as follows, based on the damage evolution index calculation described in the previous section.
- and
- The elasticity modulus and opening corresponding to Mode .
- Thickness defined in the PCOHE entry.
This actual traction is then subsequently used for the solution.
Cohesive Element Erosion
When damage evoluation index of all integration points in a cohesive element reaches the value defined on the MXDMG field in MCOHED card, and none of these integration points is in compression, the cohesive element is eroded and does not work in the rest of the analysis in the current subcase and the continued subcases.
Modeling Techniques
- Element-based technique (CIFHEX/CIFPEN elements)
- Contact-based technique (CONTACT entry)
Element-based Technique (CIFHEX and CIFPEN elements)
- The main focus of the CIFHEX and CIFPEN elements is the relative movement between the top and bottom faces.
- The relative displacement between the nodes of the top and bottom faces at
each integration point in each of the three directions (elemental X, Y, Z)
determines the cohesive opening.
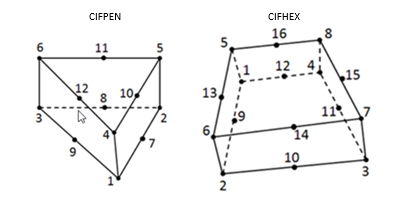
Figure 6. - Traction provides the tensile and shear stiffness and SFC
field on the PCOHE entry identifies the compressive
stiffness for cohesive elements.Note: Traction calculation depends on the method used for adhesive/bonded interface modeling.
- Refer to Interface Elements for more information on the cohesive element formulation.
- Cohesive elements should be inserted in the path of crack propagation.
- For potential-based method, only a single layer of cohesive elements should be used.
- For damage-based method, multiple layers of cohesive elements can be used.
- CIFHEX and CIFPEN elements are available for modeling cohesive elements.
- Cohesive elements can only be connected to shell or solid elements of the base model.
- If one-to-one nodal correspondence exists along with exactly the same mesh density between the cohesive element layer and the shell/solid connecting layer of the base model, then the nodes can be shared (equivalenced) and no contact definition is required.
- If such an exact one-to-one nodal correspondence does not exist, the CONTACT(FREEZE) or TIE connection should be used to connect the cohesive elements on either top/bottom layer to the corresponding shell/solid elements of the base model.
- Cohesive elements may have a geometrical thickness in the interface. For the potential-based method, unit thickness is internally used automatically, regardless of the geometric thickness and thus, the thickness effect is excluded. For the damage-based method, the THICKNESS field on PCOHE can be used to control the thickness interpretation. It is important to use realistic value. The default value is set to 1.0.
- In some cases, it may be difficult to obtain convergence with cohesive elements. Damping stabilization can be introduced in the cohesive elements to help convergence. The damping stabilization can be defined by VED on MCOHE and MCOHED entries. Damping stabilization is currently not available in cohesive contact.
Contact-Based Technique (CONTACT entry)
The contact-based technique does not require the use of cohesive elements (CIFHEX/CIFPEN) to model the cohesive zone. This technique allows simplification of the model setup, as it eliminates the need to mesh and setup the cohesive elements.
The COHE continuation line on the CONTACT Bulk Data Entry can be used to activate the contact-based method for Cohesive Zone Modeling. The MCOHEDID field references the MCOHED identification number and; therefore, identifies the contact interface as an adhesive/bonded interface.
Only damage-based method is available for contact-based technique. Also, the thickness of the cohesive zone is internally always set to unit for this technique. Thus, the thickness effect is excluded.
Contact penalty is used to avoid penetration in compression in opening cohesive effects are activated and contact effects are ignored
Currently only SMALL sliding, frictionless, N2S/S2S contact is supported for cohesive modeling.
Supported Solution Sequences
- Nonlinear Static Analysis (SMDISP and LGDISP)
- Nonlinear Transient Analysis (SMDISP and LGDISP)
- Mass is not considered in cohesive elements.
- Linear analysis, including static, transient, buckling, and eigen mode
analysis
- Cohesive effects are not available for linear analysis.
- The initial stiffness of cohesive elements is used in linear analysis. The initial stiffness is determined by the MCOHE or MCOHED entry (the initial slope of the traction-opening curve defined in MCOHE entry or the Ki value defined in the MCOHED entry.
- There is no crack propagation/initiation.
- There are no cohesive elements related output for Linear Analysis.
- Cohesive elements are currently only supported for Implicit Analysis. Explicit Analysis is not supported.
Output
Output from the cohesive zone is currently only available in H3D format.
- Cohesive Damage Initiation Index
- This item is shown in cohesive elements and secondary surface of the cohesive contact.
- Cohesive Damage Index (Damage Evolution Index)
- This item is shown in cohesive elements and secondary surface of the cohesive contact.
- Cohesive Energy by Mode (Dissipated Cohesive Energy by Mode)
- Cohesive Energy is output in terms of 3 modes (Mode I, II, and III)
- This item is not available in cohesive contact
- Cohesive Energy per Area by Mode (Dissipated Cohesive Energy per Area by
Mode)
- Cohesive Energy per area is output in terms of 3 modes (Mode I, II, and III)
- This item is not available in cohesive contact
- Cohesive Maximum Opening in History (Maximum Opening)
- This is the maximum relative displacement in history.
- This item is not available in cohesive contact.
- Cohesive Opening(s)
- This provides the output for relative displacement in the local elemental system (Mode I, II, and III) and the basic system.
- Cohesive Status (Status)
- Indicates element loading/unloading/fail state
- 0: Loading
- 1: Unloading/Reloading
- 2: Fail
- Cohesive Traction (Traction)
- This provides the output for traction in the local elemental system (Mode I, II, and III) and the basic system.
Eroded cohesive elements are not shown in h3d output starting from the eroded analysis time of the element. Therefore, the above items are not available in eroded cohesive elements.
When contacts are used to model the cohesive zone, the output is interpreted in the following way. Cohesive traction and cohesive opening are listed in label ‘Contact Traction / Normal’, ‘Contact Traction / Tangent’, ‘Contact Deformation / Normal’ and ‘Contact Deformation/Tangent.’ In order to keep it consistent with contact pressure, cohesive normal traction is shown as negative value in ‘Contact Traction / Normal.’