| mat_ID |
材料識別子 (整数、最大10桁)
|
|
| unit_ID |
単位識別子。 (整数、最大10桁)
|
|
| mat_title |
材料のタイトル (文字、最大100文字)
|
|
|
|
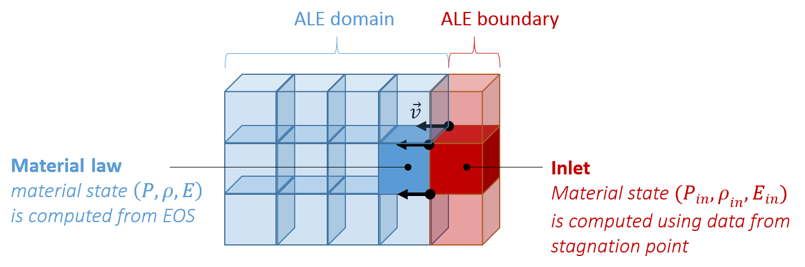
初期停滞密度 3 (実数)
|
|
|
|
E.O.S(状態方程式)で使用される基準密度 デフォルト
(実数)
|
|
| Ityp |
境界条件タイプ 1
- = 0
- 気体流入(停滞点データから)
- = 1
- 液体流入(停滞点データから)
- = 2
- 一般流入 / 流出
- = 3
- サイレント境界
(整数)
|
|
| Psh |
圧力シフト 2 (実数)
|
|
| FscaleT |
時間スケールファクター 3 (実数)
|
|
| C1node_IDv |
速度計算用の節点識別子 4
- = 0
-
- > 0
-
(整数)
|
|
| C1 |
液体の弾性率 9 (実数)
|
|
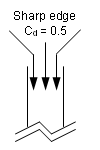
| Cd |
流量係数 5 デフォルト = 0.0(実数)
|
|
| fct_ID
|
停滞密度用の関数
識別子 3
- = 0
-
- > 0
-
(整数)
|
|
| fct_IDp |
停滞圧力用の関数
識別子 3
- = 0
-
- > 0
-
(整数)
|
|
|
|
初期停滞圧力 3 (実数)
|
|
|
|
停滞点での初期比体積エネルギー 38 (実数)
|
|
|
|
初期乱流エネルギー (実数)
|
|
|
|
初期乱流散逸 (実数)
|
|
| fct_IDk |
乱流モデリングの関数
識別子
- = 0
-
- > 0
-
(整数)
|
|
| fct_ID
|
関数
の識別子
- = 0
-
- > 0
-
(整数)
|
|
|
|
乱流粘性係数 デフォルト = 0.09(実数)
|
|
|
|
kパラメータの拡散係数 デフォルト = 1.00(実数)
|
|
|
|
パラメータの拡散係数 デフォルト = 1.30(実数)
|
|
|
|
層流プラントル数(デフォルトは0.7)と乱流プラントル数(デフォルトは0.9)の比率 (実数)
|
|
| fct_IDT |
流入温度用の関数
識別子
- = 0
- T =
Tneighbor
- = n
-
(整数)
|
|
| fct_IDQ |
流入熱流束用の関数
識別子
- = 0
- 強制流束なし
- = n
-
(整数)
|
|